直角三角形的性质应用-浙教版数学八年级上册培优训练
试卷更新日期:2025-10-29 类型:复习试卷
一、选择题
-
1. 如图,折叠直角三角形纸片的直角,使点C落在AB边上的点E处,已知BC=12, ∠B=30°则 DE的长为( )
 A、3 B、3.5 C、4 D、4.52. 如图,中,D为中点,E在上,且 . 若 , 则的长度是( )
A、3 B、3.5 C、4 D、4.52. 如图,中,D为中点,E在上,且 . 若 , 则的长度是( ) A、 B、8 C、 D、3. 如图,在中, , , 动点在线段上,以为边在右侧作等腰 , 使 , , 点为边上动点,连接 , 则周长的最小值为( )
A、 B、8 C、 D、3. 如图,在中, , , 动点在线段上,以为边在右侧作等腰 , 使 , , 点为边上动点,连接 , 则周长的最小值为( ) A、 B、 C、 D、4. 如图,在中, , 边上的中线 . 过点A作于点E,记长为x,长为y.当x,y的值发生变化时,下列代数式的值不变的是( )
A、 B、 C、 D、4. 如图,在中, , 边上的中线 . 过点A作于点E,记长为x,长为y.当x,y的值发生变化时,下列代数式的值不变的是( ) A、 B、 C、 D、5. 如图,已知 , , , 其中点 , , 分别为斜边 , , 的中点,连接 , , . 则线段 , , 的数量关系是( )
A、 B、 C、 D、5. 如图,已知 , , , 其中点 , , 分别为斜边 , , 的中点,连接 , , . 则线段 , , 的数量关系是( ) A、 B、 C、 D、6. 如图,已知平分 , , , , 于点D,于点E.如果点M是的中点,那么的长是( )
A、 B、 C、 D、6. 如图,已知平分 , , , , 于点D,于点E.如果点M是的中点,那么的长是( ) A、1 B、 C、 D、
A、1 B、 C、 D、二、填空题
-
7. 如图,在中, , 将沿对折,使点B与点A重合,若 , , 则的长度是 .
 8. 如图,在△ABC中,∠ACB=90°,CD是AB边上的中线,DE∥BC,CE平分∠DCB,BC=12,AC=16,则DE的长是.
8. 如图,在△ABC中,∠ACB=90°,CD是AB边上的中线,DE∥BC,CE平分∠DCB,BC=12,AC=16,则DE的长是. 9. 如图,在 中, 于点 于点 ,并且点 是 的中点,的周长是 ,则 的长是。
9. 如图,在 中, 于点 于点 ,并且点 是 的中点,的周长是 ,则 的长是。 10. 如图,在中, , , , 点D是线段中点, , , 下列结论:① . ②为等边三角形.③ . ④ . 其中正确的是(填序号) .
10. 如图,在中, , , , 点D是线段中点, , , 下列结论:① . ②为等边三角形.③ . ④ . 其中正确的是(填序号) . 11. 如图,在中,是边上的高线,是边上的中线,于点G,且 . 若 , 则的度数是 .
11. 如图,在中,是边上的高线,是边上的中线,于点G,且 . 若 , 则的度数是 .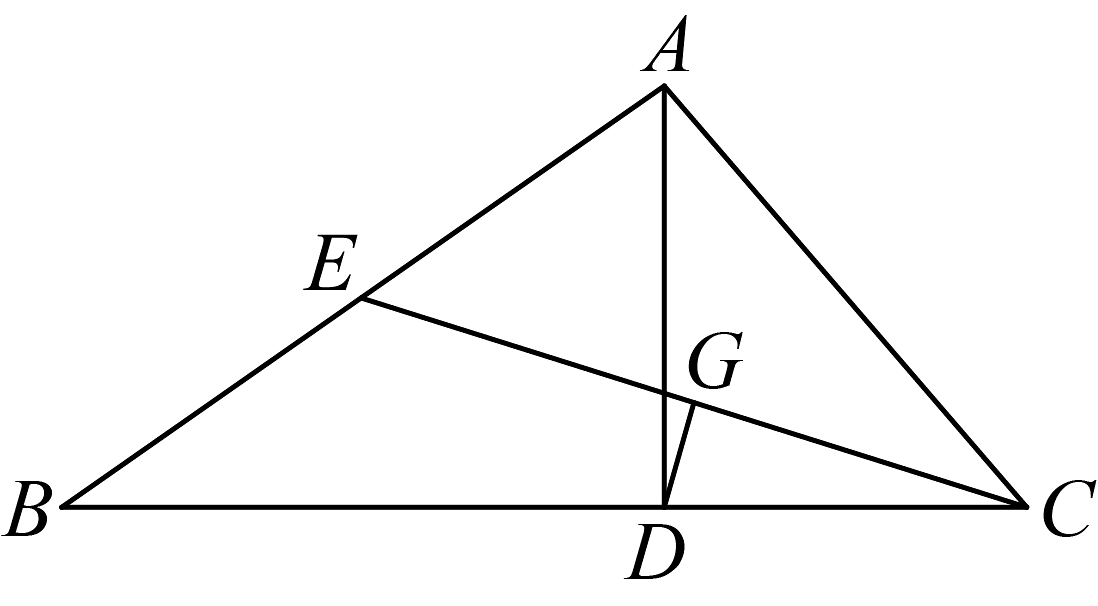 12. 如图,已知和均为等边三角形,点O是的中点,点D在射线上,连结 , 则 , 若 , 则的最小值= .
12. 如图,已知和均为等边三角形,点O是的中点,点D在射线上,连结 , 则 , 若 , 则的最小值= .
三、解答题
-
13. 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AB=1.5。D为斜边AB的中点,连结CD。求AC,CD的长。
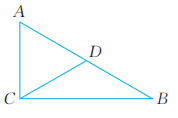 14. 如图,在中, , , 平分 .
14. 如图,在中, , , 平分 . (1)、若 , 求的长;(2)、若为的中点,连接交于点 , 求证:垂直平分 .
(1)、若 , 求的长;(2)、若为的中点,连接交于点 , 求证:垂直平分 .

