沪科版数学八年级上册全等三角形之倍长中线、角平分线模型
试卷更新日期:2025-10-29 类型:同步测试
一、倍长中线(直接倍长)
-
1. 如图,在△ABC中,∠ACB=120°,BC=4,D为AB的中点,DC⊥BC,求AC的长.

解:延长CD到H,使DH=CD,连接AH,
∵DC⊥BC,∴∠BCD=90°,( ▲ )
∵∠ACB=120°,∴∠ACD=30°,
∵D为AB的中点,∴AD=BD,( ▲ )
在△ADH与△BDC中,
∴△ADH≌△BDC(SAS),
∴AH= BC=4,( ▲ )
∠H=∠BCD=90°,( ▲ )
∵∠ACH=30°,
∴AC=8.( ▲ )
2. 如图,已知△ABC 中,AB=AC,D 为AB 上一点,E为AC 延长线上一点,BD=CE,DE 交BC于点F.求证:DF=EF.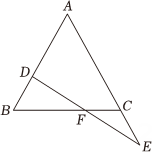 3. 如图
3. 如图 (1)、问题提出:在△ABC中,AB=5,AC=9,求BC边上的中线AD的取值范围.
(1)、问题提出:在△ABC中,AB=5,AC=9,求BC边上的中线AD的取值范围.思维点播:延长中线至等长,构造全等三角形,把AB、AC、2AD集中在△ACE中,利用
三边关系,可得AD的取值范围.
问题解决1:在图1中找出AB与 CE的数量关系并证明.:
问题解决2:AD的取值范围是 , AB和CE的位置关系是 .
(2)、问题拓展:如图2,AD是△ABC的中线,AB=AM,AC=AN,∠BAM=∠NAC=90°,探究线段AD与MN的数量关系并加以证明.二、倍长中线(间接倍长)
-
4. 在通过构造全等三角形解决的问题中,有一种方法叫倍长中线法.



图1 图2 图3
(1)、如图1,是的中线, , , 求的取值范围.我们可以延长到点M , 使 , 连接 , 根据可证 , 所以.接下来,在中利用三角形的三边关系可求得的取值范围,从而得到中线的取值范围是:;
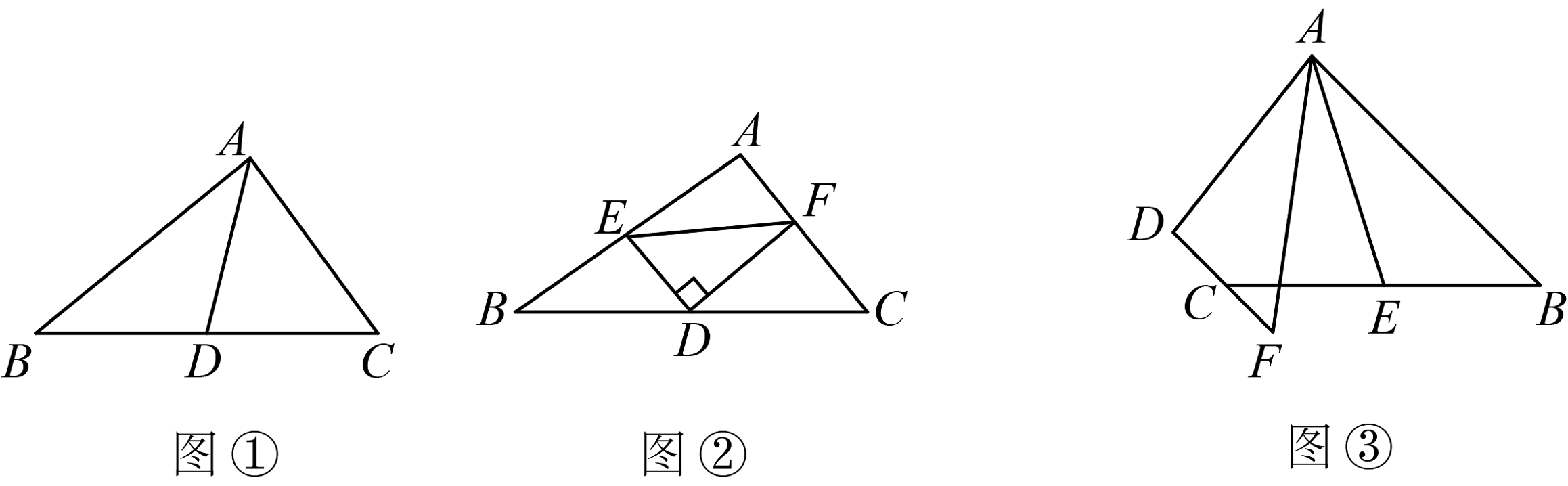
(2)、如图2,是的中线,点E在边上,交于点F , 且 , 请参考(1)中的方法求证:;(3)、如图3,在四边形中, , 点E是的中点,连接 , , 且 , 试猜想线段 , , 之间的数量关系,并予以证明.5. (1)如图①,在中,若 , , 为边上的中线,求的取值范围;(2)如图②,在中,点D是的中点, , 交于点E,交于点F,连接 , 判断与的大小关系并证明;
(3)如图③,在四边形中, , 与的延长线交于点F,点E是的中点,若是的角平分线.试探究线段 , , 之间的数量关系,并加以证明.
三、角平分线(基础全等)
-
6. 如图,AB=AC, BD=CD. 求证: AD平分∠BAC.
 7. 工人师傅常借助“角尺”这个工具来平分一个角,其背后的依据就是全等三角形的性质如图,在∠AOB的两边OA、OB上分别取OC=OD,适当摆放角尺(图中的∠CED),使其两边分别经过点C、D,且点C、D处的刻度相同,这时经过角尺顶点E的射线OE就是∠AOB的平分线.这里判定两个三角形全等的依据是( )
7. 工人师傅常借助“角尺”这个工具来平分一个角,其背后的依据就是全等三角形的性质如图,在∠AOB的两边OA、OB上分别取OC=OD,适当摆放角尺(图中的∠CED),使其两边分别经过点C、D,且点C、D处的刻度相同,这时经过角尺顶点E的射线OE就是∠AOB的平分线.这里判定两个三角形全等的依据是( ) A、SAS B、SSS C、AAS D、ASA8. 如图,于于F,若 ,
A、SAS B、SSS C、AAS D、ASA8. 如图,于于F,若 ,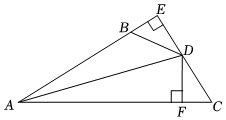 (1)、求证:平分;(2)、已知 , 求的长.9. 如图,在 中,D是 边上的一点, , 平分 ,交 边于点E,连接 .
(1)、求证:平分;(2)、已知 , 求的长.9. 如图,在 中,D是 边上的一点, , 平分 ,交 边于点E,连接 . (1)、求证: ;(2)、若 , ,求 的度数.10. 如图,在△ABC中,AB<AC,边的垂直平分线交的外角的平分线于点 , 垂足为E,DF⊥AC于点F,于点 , 连接CD.
(1)、求证: ;(2)、若 , ,求 的度数.10. 如图,在△ABC中,AB<AC,边的垂直平分线交的外角的平分线于点 , 垂足为E,DF⊥AC于点F,于点 , 连接CD. (1)、求证:BG=CF;(2)、若AB=10cm,AC=14cm,求AG的长.
(1)、求证:BG=CF;(2)、若AB=10cm,AC=14cm,求AG的长.四、角平分线(构造全等)
-
11. 如图,在△ABC中,∠ACB=2∠B .
 (1)、如图1,当∠C=90°, AD为∠BAC的角平分线时,求证:AB=AC+CD ;(2)、如图2,当 ∠C≠90°, AD为 ∠BAC的角平分线时,线段AB , AC , CD的数量关系为 ;(3)、如图3,当AD为△ABC的外角平分线时,线段AB , AC , CD 的数量关系为 ;12. 在△ABC中,∠ACB=2∠B,如图①,当∠C=90°,AD为∠BAC的角平分线时,在AB上截取AE=AC,连结DE,易证AB=AC+CD.
(1)、如图1,当∠C=90°, AD为∠BAC的角平分线时,求证:AB=AC+CD ;(2)、如图2,当 ∠C≠90°, AD为 ∠BAC的角平分线时,线段AB , AC , CD的数量关系为 ;(3)、如图3,当AD为△ABC的外角平分线时,线段AB , AC , CD 的数量关系为 ;12. 在△ABC中,∠ACB=2∠B,如图①,当∠C=90°,AD为∠BAC的角平分线时,在AB上截取AE=AC,连结DE,易证AB=AC+CD.

 (1)、如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB,AC,CD又有怎样的数量关系?不需要证明,请直接写出你的猜想;(2)、如图③,当AD为△ABC的外角平分线时,线段AB,AC,CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.13. 如图,已知为的角平分线,延长到 , 使得 , 连接 , 若 , 且 .
(1)、如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB,AC,CD又有怎样的数量关系?不需要证明,请直接写出你的猜想;(2)、如图③,当AD为△ABC的外角平分线时,线段AB,AC,CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.13. 如图,已知为的角平分线,延长到 , 使得 , 连接 , 若 , 且 . (1)、求证:平分;(2)、求的取值范围;(3)、若延长 , 相交于点 , 求的度数.
(1)、求证:平分;(2)、求的取值范围;(3)、若延长 , 相交于点 , 求的度数.

