北师大版九年级上学期期中模拟数学试题(范围:第1-4章)
试卷更新日期:2025-10-28 类型:期中考试
一、选择题(每题3分,共30分)
-
1. 把方程化成的形式,则( )A、17 B、14 C、11 D、72. 如图,正方形内接于 , 点在上,点分别在和边上,且上的高 , , 则正方形的边长为( )
 A、6 B、5 C、4 D、33. 10月16日是世界粮食日.某校组织了粮食安全公益活动,现有“节粮宣讲员”、“光盘示范员”和“爱粮监督员”三类志愿者岗位身份,小霞和小艺从中任选一类,则她们恰好选到同一类岗位的概率是( )A、 B、 C、 D、4. 如图,是等边三角形,被一平行于的矩形所截(即:FG∥BC),若AB被截成三等分,则图中阴影部分的面积是的面积的( )
A、6 B、5 C、4 D、33. 10月16日是世界粮食日.某校组织了粮食安全公益活动,现有“节粮宣讲员”、“光盘示范员”和“爱粮监督员”三类志愿者岗位身份,小霞和小艺从中任选一类,则她们恰好选到同一类岗位的概率是( )A、 B、 C、 D、4. 如图,是等边三角形,被一平行于的矩形所截(即:FG∥BC),若AB被截成三等分,则图中阴影部分的面积是的面积的( ) A、 B、 C、 D、5. 对于一元二次方程(a≠0),下列说法:
A、 B、 C、 D、5. 对于一元二次方程(a≠0),下列说法:①若 , 则;
②若方程有两个不相等的实数根,则方程必有两个不相等的实数根;
③若是方程的一个根,则一定有成立;
④若是一元二次方程的根,则
其中正确的个数为( )
A、4 B、3 C、2 D、16. 某经济技术开发区今年一月份工业产值达50亿元,且一月份、二月份、三月份的总产值为亿元,若设平均每月的增长率为 , 根据题意可列方程( )A、 B、 C、 D、7. 如图,在菱形中,分别是上的点,且与相交于点O.若 , 则的度数为( ) A、 B、 C、 D、8. 如图,在矩形中,E在边上,将沿折叠,使点A恰好落在矩形的对称中心O处, , 则的长是( )
A、 B、 C、 D、8. 如图,在矩形中,E在边上,将沿折叠,使点A恰好落在矩形的对称中心O处, , 则的长是( ) A、 B、 C、8 D、129. 如图,点在正方形的对角线上,于点 , 连接并延长,交边于点 , 交边的延长线于点 . 若 , , 则( )
A、 B、 C、8 D、129. 如图,点在正方形的对角线上,于点 , 连接并延长,交边于点 , 交边的延长线于点 . 若 , , 则( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共15分)
-
10. 如图,在菱形中, , , 动点、分别在线段、上,且 , 则的最小值为 .
 11. 若是一元二次方程的两个实数根,多项式的值是 .12. 一个盒子中装有10颗黄色幸运星,若干颗红色幸运星和16颗蓝色幸运星,小明通过多次摸取幸运星试验后发现,摸取到红色幸运星的频率稳定在0.5左右,则红色幸运星颗数约为颗.13. 如图,取一张长为 ,宽为 的矩形纸片 ,将它对折两次后得到一张小矩形纸片.若要使小矩形与原矩形相似,则原矩形纸片的边 应满足的条件是 .
11. 若是一元二次方程的两个实数根,多项式的值是 .12. 一个盒子中装有10颗黄色幸运星,若干颗红色幸运星和16颗蓝色幸运星,小明通过多次摸取幸运星试验后发现,摸取到红色幸运星的频率稳定在0.5左右,则红色幸运星颗数约为颗.13. 如图,取一张长为 ,宽为 的矩形纸片 ,将它对折两次后得到一张小矩形纸片.若要使小矩形与原矩形相似,则原矩形纸片的边 应满足的条件是 . 14. 某地进行“迎国庆振兴杯”篮球邀请赛,赛制为单循环(每两队之间赛一场),若计划安排21场比赛,则邀请个球队参赛.
14. 某地进行“迎国庆振兴杯”篮球邀请赛,赛制为单循环(每两队之间赛一场),若计划安排21场比赛,则邀请个球队参赛.三、解答题(共8题,共75分
-
15. 解方程∶(1)、;(2)、 .16. 已知关于的方程 .(1)、求证:无论为何值,方程总有实数根;(2)、若方程的两个实数根为 , , 求代数式的值.17. 如图,矩形中,点P , Q分别为边上的点, . BD平分 .
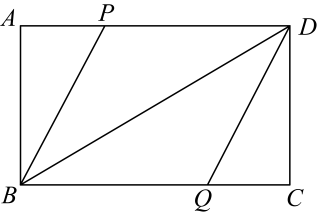 (1)、求证:四边形为菱形;(2)、若 , , 求四边形的面积.18. 如图,在中,分别是的中点.
(1)、求证:四边形为菱形;(2)、若 , , 求四边形的面积.18. 如图,在中,分别是的中点. (1)、求证:四边形是矩形;(2)、若 , 求的面积.19. 如图,是的角平分线,在边上取点 , 使 .
(1)、求证:四边形是矩形;(2)、若 , 求的面积.19. 如图,是的角平分线,在边上取点 , 使 . (1)、求证: .(2)、若 , , 求的度数.20. 暑假期间某景区商店推出销售纪念品活动,已知纪念品每件的进货价为30元,经市场调研发现,当该纪念品的销售单价为40元时,每天可销售280件;当销售单价每增加1元,每天的销售数量将减少10件.(销售利润=销售总额-进货成本)(1)、若该纪念品的销售单价为45元时则当天销售量为 件.(2)、当该纪念品的销售单价为多少元时,该产品的当天销售利润是2610元.(3)、该纪念品的当天销售利润有可能达到3700元吗?若能,请求出此时的销售单价;若不能,请说明理由.21. 某校开展了学习党史的知识竞赛活动.初三年级学生的比赛成绩根据结果分为 , , , 四个等级.其等级对应的分值分别为100分分、90分8分、80分分、70分及以下.现将初三学生的最后等级成绩分析整理绘制得到了两幅不完整的统计图,请根据图中的信息解决下面的问题.
(1)、求证: .(2)、若 , , 求的度数.20. 暑假期间某景区商店推出销售纪念品活动,已知纪念品每件的进货价为30元,经市场调研发现,当该纪念品的销售单价为40元时,每天可销售280件;当销售单价每增加1元,每天的销售数量将减少10件.(销售利润=销售总额-进货成本)(1)、若该纪念品的销售单价为45元时则当天销售量为 件.(2)、当该纪念品的销售单价为多少元时,该产品的当天销售利润是2610元.(3)、该纪念品的当天销售利润有可能达到3700元吗?若能,请求出此时的销售单价;若不能,请说明理由.21. 某校开展了学习党史的知识竞赛活动.初三年级学生的比赛成绩根据结果分为 , , , 四个等级.其等级对应的分值分别为100分分、90分8分、80分分、70分及以下.现将初三学生的最后等级成绩分析整理绘制得到了两幅不完整的统计图,请根据图中的信息解决下面的问题. (1)、由图可知该校初三共 名学生,比赛成绩等级为级的学生人数是 人;(2)、由图可知的值为 ;(3)、初三年级本次比赛获得满分的4人中有2个男生和2个女生,现从这4个学生中随机选2人参加学校决赛,若每个学生被抽取的可能性相等,请用画树状图或者列表法求抽取的人中至少有1个女生的概率.22. 综合与实践
(1)、由图可知该校初三共 名学生,比赛成绩等级为级的学生人数是 人;(2)、由图可知的值为 ;(3)、初三年级本次比赛获得满分的4人中有2个男生和2个女生,现从这4个学生中随机选2人参加学校决赛,若每个学生被抽取的可能性相等,请用画树状图或者列表法求抽取的人中至少有1个女生的概率.22. 综合与实践
【问题提出】
勾股定理和黄金分割是几何学中的两大瑰宝,其中"贵金分割"给人以美感.课本第56页这样定义"黄金分割点":如图1,点将线段AB分成两部分 , 若 , 则称点为线段AB的黄金分割点,这个比值称为黄金比.
(1)、【初步感知】如图1,若 , 求临金比的值.
(2)、【类比探究】如图2,在中,是BC边上一点,AD将分割成两个三角形(),若 , 则称AD为的黄金分割线.
①求证:点D是线段BC的黄金分割点:
②若△ABC的面积为4,求△ACD的面积.
(3)、【拓展应用】如图3,在中,为A,B上的一点(不与A,B重合),过D作DE∥BC,交AC于E,BE,CD相交于 , 连接AF并延长,与DE,BC分别交于M,N.请问直线AN是的黄金分割线吗?并说明理由.