勾股定理的翻转问题-浙教版数学八年级上册培优训练

试卷更新日期：2025-10-28 类型：复习试卷

进入出卷网下载

一、选择题

1. 如图， $Rt △ A B C$ 中， $∠ A = 90 °$ ， $A B = 6$ ， $A C = 8$ ，现将 $△ A B C$ 沿 $B D$ 进行翻折，使点 $A$ 刚好落在 $B C$ 上，则 $C D$ 的长为（）

A、5 B、 $\frac{4}{5}$ C、4 D、3

查看试题解析
2. 如图，Rt△ABC，∠A=90°，将△ABC沿DE翻折，使得点C与点B重合。若AB=6，AC=8，则折痕 DE 的长为（）

A、4 B、 $\frac{15}{4}$ C、5 D、 $\frac{25}{4}$

查看试题解析

二、填空题

3. 如图所示，将三角形纸片ABC沿AD折叠，使点C落在BD边上的点E处.若∠C=45°，∠B=30°，AD=2，则. $A B^{2} - A C^{2}$ 的值是.

查看试题解析
4. 如图，△AOB中，∠AOB=90°，OA=5，OB=8，点M为AB的中点，C为边OB上一点，把△AOC沿直线AC翻折得到△ACD.

(1)、当点D恰好落在 AB边上时，DM的长为.

(2)、当MD与△AOB 的边平行时，OC 的长为.

查看试题解析
5. 如图，在 $△ A B C$ 中， $A B = A C$ ，点D在 $△ A B C$ 内， $A D$ 平分 $∠ B A C$ ，连接 $C D$ ，把 $△ A D C$ 沿 $C D$ 折叠， $A C$ 落在 $C E$ 处交 $A B$ 于F，恰有 $C E ⊥ A B$ ．若 $B C = 10$ ， $A D = 7$ ，则 $E F =$ ．

查看试题解析
6. 如图，在 $Rt △ A B C$ 中， $∠ B = 90 °$ ， $A B = 6$ ， $B C = 8$ ，将 $△ A B C$ 折叠，使点B恰好落在边 $A C$ 上，与点 $B^{'}$ 重合， $A E$ 为折痕，则 $E B^{'} =$ ．

查看试题解析
7. 如图， $Rt △ A B C$ 的纸片中， $∠ C = 90 ° ， A C = 5 ， B C = 12$ ，点D在边 $B C$ 上，以 $A D$ 为折痕将 $△ A D B$ 折叠得到 $△ A D B^{'}$ ， $A B^{'}$ 与边 $B C$ 交于点 $E$ ，若 $△ D E B^{'}$ 为直角三角形，则 $B D$ 的长为．

查看试题解析
8. 如图，在 $△ A B C$ 中， $A C = 10 cm$ ， $A B = 16 cm$ ， $∠ B A C = ∠ B$ ， $P$ 是线段 $A B$ 上一动点，将 $△ B C P$ 沿直线 $C P$ 折叠，使点 $B$ 落在点 $D$ 处， $C D$ 交 $A P$ 于点 $E$ ．
（1） $C D$ 的长为．
（2）当 $△ A C E$ 是直角三角形时， $B P$ 的长为．

查看试题解析
9. 如图，在 $△ A B C$ 中， $∠ A B C = 30 °$ ， $A B = A C = 2 \sqrt{3}$ ，点 $D$ 是边 $B C$ 上的点，将 $△ A C D$ 沿 $A D$ 折叠得到 $△ A E D$ ，点 $E$ 是点 $C$ 的对称点．若 $∠ C D E$ 为 $120 °$ ，则 $C D$ 的长是．

查看试题解析
10. 如图，在直角三角形纸片 $A B C$ 中， $∠ A C B = 90 °$ ， $A C = 3$ ， $B C = 4$ ，点 $D$ 在边 $A B$ 上，以 $C D$ 为折痕将 $△ C B D$ 折叠得到 $△ C F D$ ， $C F$ 与边 $A B$ 交于点 $E$ ，当 $D F ⊥ A B$ 时， $B D$ 的长是

查看试题解析
11. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，点 $D$ ， $E$ 分别在 $A C$ ， $B C$ 上，且 $∠ C D E = ∠ B$ ，将 $△ C D E$ 沿 $D E$ 折叠，点 $C$ 恰好落在 $A B$ 边上的点 $F$ 处， $C F$ 与 $D E$ 交于点 $G$ ．下列结论：其中正确的结论有．（填序号）
$①$ $A B = 2 C F$ ；
$②$ 若 $∠ A B C = 50 °$ ，则 $∠ A F D = 60 °$ ；
$③$ 若 $C D = 1.5$ ， $C E = 2$ ，则 $D G \cdot G E = 1.2$ ；
$④$ 若 $A C = 4$ ， $B C = 3$ ，则 $C G = 1.25$ ．

查看试题解析
12. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，点D为 $A B$ 边上一点，连接 $C D$ ．现将 $△ A C D$ 沿 $C D$ 翻折使得点A落在 $A B$ 边的中点E处．若 $B C = 6$ ，则 $B D =$ ．

查看试题解析
13. 如图，在 $Rt △ A B C$ 中， $∠ B = 30 °, A C = 3, A D$ 是 $∠ B A C$ 的平分线，交 $B C$ 于点 $D$ ，点 $E$ 在 $A B$ 上，将 $△ B D E$ 沿 $D E$ 对折，点 $B$ 的对称点为点 $F$ ．当 $E F$ 与 $Rt △ A B C$ 的一边平行时，则 $B E$ 的长为．

查看试题解析

三、解答题

14. 如图，直角三角形纸片的两直角边 $A C = 6$ ， $B C = 8$ ，现将直角边 $A C$ 沿 $A D$ 折叠，使它落在斜边 $A B$ 上，点C与点E重合，求 $C D$ 的长．

查看试题解析
15. 如果三角形的两个内角a与β满足2a+β＝90°，那么我们称这样的三角形为“准互余三角形”．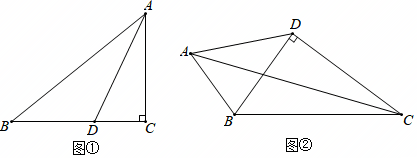

(1)、基础巩固：
若△ABC是“准互余三角形”，∠C＞90°，∠A＝60°，则∠B＝°；

(2)、尝试应用：
如图①，在Rt△ABC中，∠ACB＝90°，∠BAC＝50°．
①若AD是∠BAC的平分线，判断△ABD是否是“准互余三角形” ▲ （是、否）；
②在边BC上存在点E（异于点D），使得△ABE也是“准互余三角形”，求此时∠EAC的度数；

(3)、拓展提高：
如图②，在四边形ABCD中，AB=7，CD=12，BD⊥CD ， ∠ABD=2∠BCD ，且△ABC是“准互余三角形”，求对角线AC的长．

查看试题解析
16. 如图，在 $Rt △ A B C$ 中， $∠ C = 90 °, A B = 10, B C = 8$ ，点D在 $B C$ 上，将 $△ A D C$ 沿直线 $A D$ 翻折，形成 $△ A D C^{'}$ ．

(1)、若 $A C^{'} ∥ C D$ ，求 $∠ C A D$ 的度数；

(2)、若点C的对称点恰好落在 $A B$ 上，求线段 $B D$ 的长．

查看试题解析
17. 如图1，已知在 $Rt △ A B C$ 中， $∠ A B C = 90 °$ ，已知 $B C = 15$ ， $A B = 20$ ． $D$ 是边 $A C$ 上一动点，连接 $B D$ ，以 $B D$ 为对称轴将 $△ C B D$ 翻折至 $△ C^{'} B D$ ．

(1)、若 $C^{'} D ∥ B C$ 时．
①求证： $C B = C D$ ；
②求折痕 $B D$ 的长．

(2)、如图2，若 $C^{'} D ⊥ B C$ 时，以 $B$ 为原点，直线 $B C$ 为 $x$ 轴，建立平面直角坐标系，求此时 $C^{'}$ 的坐标．

查看试题解析
18. 如图1，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $B C = 4$ ，点D在 $A B$ 边上运动， $△ C D B$ 沿着 $C D$ 折叠得到 $△ C D B^{'}$ ，直线 $C B^{'}$ 与直线 $A B$ 相交于 $E$ 点．

(1)、如图2，若 $A C = 3$ ， $C B^{'} ⊥ A B$ ，求 $C E$ 的长度；

(2)、当 $△ A B^{'} C$ 为等腰直角三角形时，求 $A C$ 的值；

(3)、若 $A C = 3$ ， $△ E D B^{'}$ 为钝角三角形，直接写出 $B D$ 长度的取值范围．

查看试题解析
19. 定义：若 $a ， b ， c$ 是 $△ A B C$ 的三边，且 $a^{2} + b^{2} = 2 c^{2}$ ，则称 $△ A B C$ 为“方倍三角形”．

(1)、若 $Rt △ A B C$ 是“方倍三角形”，且斜边AB= $\sqrt{3}$ ，则该三角形的面积为____．

(2)、如图， $△ A B C$ 是“方倍三角形”，且 $A B = A C$ ，求证： $△ A B C$ 为等边三角形．

(3)、如图， $△ A B C$ 中， $∠ A B C = 120^{\circ}$ ， $∠ A C B = 45^{\circ}$ ， $p$ 是 $A C$ 边上一点，将 $△ A B P$ 沿 $B P$ 进行折叠，点 $A$ 落在点 $D$ 处，连接 $C D$ ， $A D$ ，若 $△ A B D$ 为“方倍三角形”，且 $A P = \sqrt{2}$ ，求 $P C$ 的长．

查看试题解析
20. 自定义：若 $a, b, c$ 是 $△ A B C$ 的三边，且满足 $a^{2} + b^{2} = 2 c^{2}$ ，则称 $△ A B C$ 为“美眉三角形”

(1)、你认为等边三角形、直角三角形、等腰三角形、等腰直角三角形中一定是“美眉三角形”的有_____________．

(2)、若 $Rt △ A B C$ 是“美眉三角形”，且斜边 $A B = 2 \sqrt{3}$ ，则该三角形的面积为_____________．

(3)、如图， $△ A B C$ 中， $∠ A B C = 120 °, ∠ A C B = 45 °$ ， P为 $A C$ 边上一点，将 $△ A B P$ 沿直线 $B P$ 进行折叠，点 $A$ 落在点 $D$ 处，连接 $C D, A D$ ．若 $△ A B D$ 为“美眉三角形”，且 $A P = \sqrt{2}$ ，求 $△ P D C$ 的面积．

查看试题解析