勾股定理的设元计算-浙教版数学八年级上册培优训练

试卷更新日期：2025-10-28 类型：复习试卷

进入出卷网下载

一、单选题

1. 九章算术中记载了一个“折竹抵地”问题：今有竹高一丈，末折抵地，去本三尺，问折者高几何？题意是：一根竹子原高1丈（1丈 $= 10$ 尺），中部有一处折断，竹稍触地面处离竹根4尺，试问折断处离地面多高？则折断处离地面的高度为（）

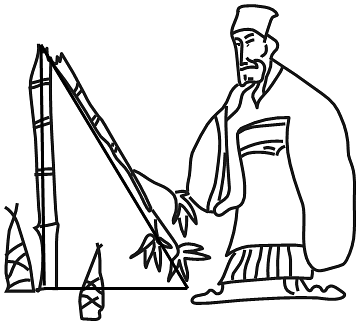A、4.55尺 B、5.45尺 C、4.2尺 D、5.8尺

查看试题解析
2. 在我国古代数学名著《算法统宗》里有一道“荡秋千”的问题：“平地秋千未起，踏板一尺离地．送行二步与人齐，五尺人高曾记．仕女佳人争蹴，终朝笑语欢嬉．良工高士素好奇，算出索长有几？”译文：“有一架秋千，当它静止时，踏板离地1尺，将它往前推送10尺（水平距离）时，秋千的踏板就和身高为5尺的人一样高，秋千的绳索始终是拉直的，试问绳索有多长？”设绳索长为x尺，则x满足的方程为（）

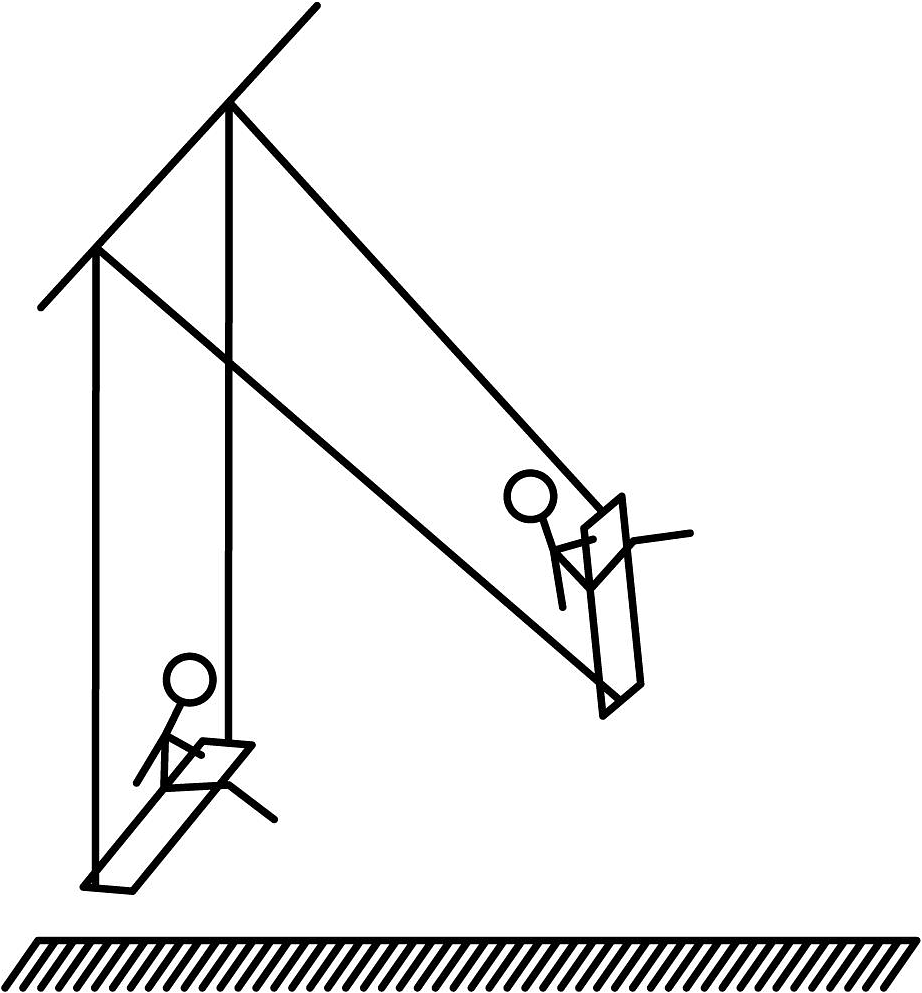A、x²=10²+（x-5-1）² B、x²＝（x﹣5）²+10² C、x²＝10²+（x+1-5）² D、x²＝（x+1）²+10²

查看试题解析
3. 如图，在一块平地上，一棵高16m的大树从离地面6m处折断倒下，则倒下的树顶到树底部的距离是( )

A、6m B、8m C、10m D、16m

查看试题解析
4. 如图甲所示，长、宽均为3，高为8的长方体容器放在水平桌面上，里面盛有水，水面高度为6，绕底面一棱进行旋转倾斜后，水面恰好触到容器口边缘，图乙是此时情景的平面示意图，则水面的高度为（ )

A、 $\frac{24}{5}$ B、 $\frac{32}{5}$ C、 $\frac{12 \sqrt{34}}{17}$ D、 $\frac{20 \sqrt{34}}{17}$

查看试题解析

二、填空题

5. 数学经典著作《九章算术》中有一道著名的“引葭（jiā）赴岸”题：“今有池方一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐：问水深、葭长各几何？”意思为：如图，有一池塘，底面是边长为一丈（一丈等于十尺）的正方形，池的中央生有一棵芦苇，高出水面一尺，若将芦苇引到池边中点处，正好与岸边齐平，则水深为尺.

查看试题解析
6. 如图，小霞将升旗的绳子拉到旗杆底端，并在绳子上打了一个结，然后将绳子拉到离旗杆底端12米处，发现此时绳子底端距离打结处约6米，则滑轮到地面的高度为米．

查看试题解析
7. 如图，某自动感应门的正上方A处装着一个感应器，离地 $A B = 2.5$ 米，当人体进入感应器的感应范围内时，感应门就会自动打开．一个身高1.6米的学生 $C D$ 正对门，缓慢走到离门 $1.2$ 米的地方时（ $B C = 1.2$ 米），感应门自动打开，则 $A D =$ 米．

查看试题解析
8. 如图， $14 m$ 高的教学楼前有一颗 $6 m$ 高的大树，它们相距 $6 m$ ，树的顶端有一只小鸟，它要飞到楼顶上，至少要飞行 $m$ ．

查看试题解析
9. 如图，一垂直地面的木杆，在离地面 12 米处折断，木杆顶端落在离木杆底端 5 米处，则木杆折断之前的高度为米.

查看试题解析
10. 在“综合与实践”课—测量旗杆高度中，同学们发现旗杆上的绳子垂到地面还多出了2米．当把绳子向外拉直并使绳子底端刚好碰地时，经过测量此时绳子底端距离旗杆底部6米（如图所示），则旗杆的高度为米．

查看试题解析

三、解答题

11. “儿童散学归来早，忙趁东风放纸鸢”．又到了放风筝的最佳时节．某校八年级（1）班的小明和小亮学习了“勾股定理”之后，为了测得风筝的垂直高度 $C E$ ，他们进行了如下操作：①测得水平距离 $B D$ 的长为15米；②根据手中剩余线的长度计算出风筝线 $B C$ 的长为25米；③牵线放风筝的小明的身高为 $1.6$ 米．

(1)、求风筝的垂直高度 $C E$ ；

(2)、如果小明想风筝沿 $C D$ 方向下降12米，则他应该往回收线多少米？

查看试题解析
12. 数学兴趣小组测量学校旗杆的高度. 同学发现有一根系在旗杆顶端的绳子垂到了地面，并多出 1 m（如图1）. 将绳子拉紧，使绳子下端点 C 恰好接触到地面（如图2）. 现测得点 C 到旗杆 AB 的距离为 5 m，求旗杆的高度 AB.

查看试题解析
13. 学过《勾股定理》后，某数学兴趣小组来到操场上测量旗杆 $A B$ 的高度．测得从旗杆顶端垂直挂下来的升旗用的绳子比旗杆长1米（如图1），将绳子拉直时，测得拉绳子的手到地面的距离 $C D$ 为1米，到旗杆的距离 $C E$ 为6米（如图2）．

(1)、若旗杆的高度 $A B = x$ 米，那么绳子的长度可以表示为________米（用含x的代数式表示）

(2)、求旗杆 $A B$ 的高度．

查看试题解析

14. 某校“综合与实践”小组开展了测量本校旗杆高度的实践活动，他们制订了测量方案，并利用课余时间完成了实地测量，测量结果如下表（不完整）．

课题	测量学校旗杆的高度
成员	组长：XXX组员：XXX，XXX，XXX
工具	皮尺等
测量示意图		说明：线段 $A B$ 表示学校旗杆， $A B$ 垂直地面于点 $B$ ．第一次操作：如图①，将系在旗杆顶端的绳子自然下垂到地面，绳子多出的一段在地面拉直后记作 $B C$ ，用皮尺测出 $B C$ 的长度；第二次操作：如图②，将绳子拉直，绳子末端落在地面的点 $D$ 处，用皮尺测出 $B D$ 的长度．
测量数据	测量项目	数值（单位：米）
	图①中 $B C$ 的长度	1
	图②中 $B D$ 的长度	5
．．．．．．	．．．

(1)、根据以上测量结果，请你帮助这个小组求出学校旗杆

A B

的高度．

(2)、如图③，第三次操作：某同学从点

D

前行至点

F

处，再次将绳子拉直，此时测得绳子末端

E

到地面的距离

E F

的长度为1米，求该同学前进的距离

D F

的长度．

(\sqrt{3} \approx 1.73 ， 结 果 精 确 到 0 .1)

查看试题解析

15. 今有立木，系索其末，委地三尺.引索却行，去本八尺而索尽.问：索长几何?(选自《九章算术》)
题目大意：在直立于地面的一根木杆顶端系一根绳索，绳索自然下垂后拖在地面上的长度为3尺(如图).在距木杆底端8尺处的地面拉紧绳索，整根绳索恰好被拉直.这根绳索有多长?
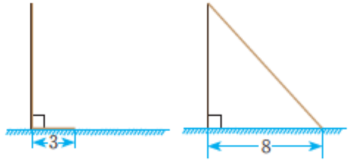
将这个问题一般化，即已知直角三角形的勾长a，弦与股的差为d，求弦长c.

(1)、试用a， d表示c；

(2)、查阅资料，了解《九章算术》解决这类问题的思路与方法.

查看试题解析