勾股定理在最短路径中的应用-浙教版数学八年级上册培优训练
试卷更新日期：2025-10-28 类型：复习试卷
一、选择题
-
1. 如图，在底面周长约为6米的石柱上，有一条雕龙从柱底沿立柱表面盘绕2圈到达柱顶正上方，每根华表刻有雕龙的部分的柱身高约16米，则雕刻在石柱上的巨龙至少为（ ）
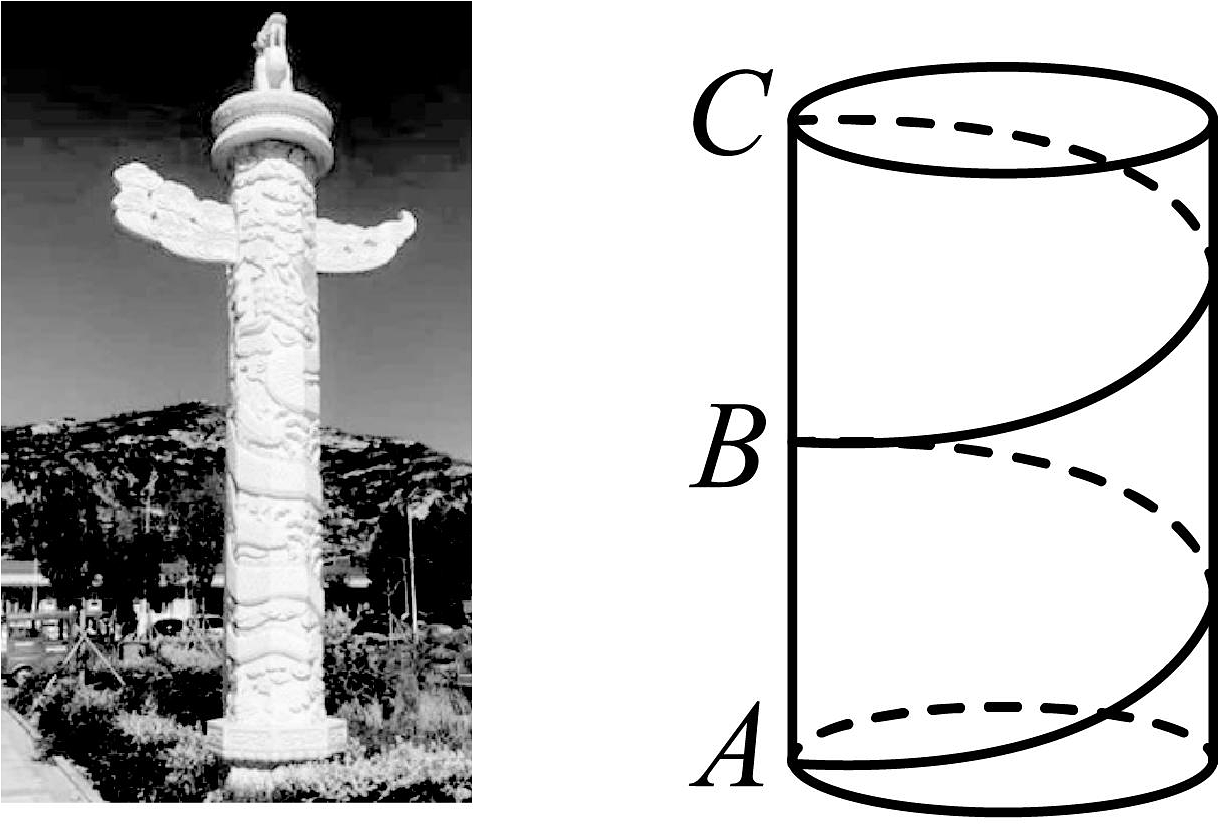A、20米 B、25米 C、30米 D、15米2. 如图，长方体的长为 ， 宽为 ， 高为 ， 点离点为 ， 一只蚂蚁如果要沿着长方体的表面从点A爬到点去吃一滴蜜糖，需要爬行的最短距离是（ ）
A、 B、 C、 D、3. 如图，透明的圆柱形容器（容器厚度忽略不计）的高为12cm，底面周长为10cm，在容器内壁离容器底部3cm的点B处有一饭粒，此时一只蚂蚁正好在容器外壁，且离容器上沿3cm的点A处，则蚂蚁吃到饭粒需爬行的最短路径是（ ）
A、13cm B、2cm C、cm D、2cm4. 如图，台阶阶梯每一层高20cm，宽30cm，长50cm，一只蚂蚁从A点爬到B点，最短路程是（ ）
A、 B、 C、120 D、1305. 如图，有一长、宽、高分别是5cm，4cm，4cm的长方体木块，一只蚂蚁沿如图所示路径从顶点A处在长方体的表面爬到长方体上和A相对的中点B处，则需要爬行的最短路径长为（ ）
A、cm B、cm C、cm D、cm6. 如图，点A，B是棱长为1的立方体的两个顶点，若将该立方体按图中所示展开，则在展开图中，A，B两点间的距离是（ ）
A、 B、 C、 D、7. 已知蚂蚁从长、宽都是3，高是8的长方形纸箱的A点沿纸箱爬到B点，那么它所行的最短路线的长是（ ）
A、8 B、10 C、12 D、16二、填空题
-
8. 如图，在中， ， ， ， 点是内一点，则点到三个顶点的距离和的最小值是 ．
9. 如图是放在地面上的一个长方体盒子，其中AB＝24cm，BC＝12cm，BF＝7cm，点M在棱AB上，且AM＝6cm，点N是FG的中点，一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N，它需要爬行的最短路程为.
10. 如图所示是长方体透明玻璃鱼缸，假设其长 AD = 80 cm，高 AB =60 cm，水深AE=40 cm.在水面上紧贴内壁G处有一块面包屑，G在水面线EF上，且EG=60cm，一只小虫想从鱼缸外的A 点沿鱼缸壁爬进鱼缸内的G处吃面包屑，则小虫爬行的最短路线长为cm.
11. 如图，圆柱形容器中，高为120cm，底面周长为100cm，在容器内壁离容器底部40cm的点B处有一蚊子，此时一只壁虎正好在容器外壁，离容器上沿40cm与蚊子相对的点A处，则壁虎捕捉蚊子的最短距离为 cm．（容器厚度忽略不计）
12. 如图是一块长、宽、高分别是6cm、4cm和3cm的长方体木块，一只蚂蚁要从顶点A出发，沿长方体的表面爬到和A相对的顶点B处吃食物，那么它需要爬行的最短路线的长是
三、解答题
-
13. 在某河流的北岸有A，B两个村子，A村距河北岸的距离为1千米，B村距河北岸的距离为4千米，且两村相距5千米.
(1)、现以河北岸为x轴，A村在y轴正半轴上(单位：千米)，建立平面直角坐标系，并描出A，B两村的位置，写出其坐标.(2)、两村商议共同在河北岸修一个水泵站，分别向两村各铺一条水管.要使所用水管最短，水泵站应修在什么位置?在图中标出水泵站的位置，并求出所用水管的长度.14. 如图，正方形ABCD，AB边上有一点E，AE=3，EB=1，在AC上有一点P，使EP+BP为最短．求：最短距离EP+BP．
