勾股定理在数轴上表示无理数-浙教版数学八年级上册培优训练
试卷更新日期:2025-10-28 类型:复习试卷
一、单选题
-
1. 如图, 在中, , , , 则数轴上点A所表示的数是( )
 A、 B、 C、 D、2. 在平面直角坐标系中,A(﹣1,0),B(0,3),以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C的横坐标在哪两个数之间( )
A、 B、 C、 D、2. 在平面直角坐标系中,A(﹣1,0),B(0,3),以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C的横坐标在哪两个数之间( ) A、0到1 B、1到2 C、2到3 D、3到43. 如图,根据尺规作图痕迹,图中标注在点A处所表示的数为( )
A、0到1 B、1到2 C、2到3 D、3到43. 如图,根据尺规作图痕迹,图中标注在点A处所表示的数为( )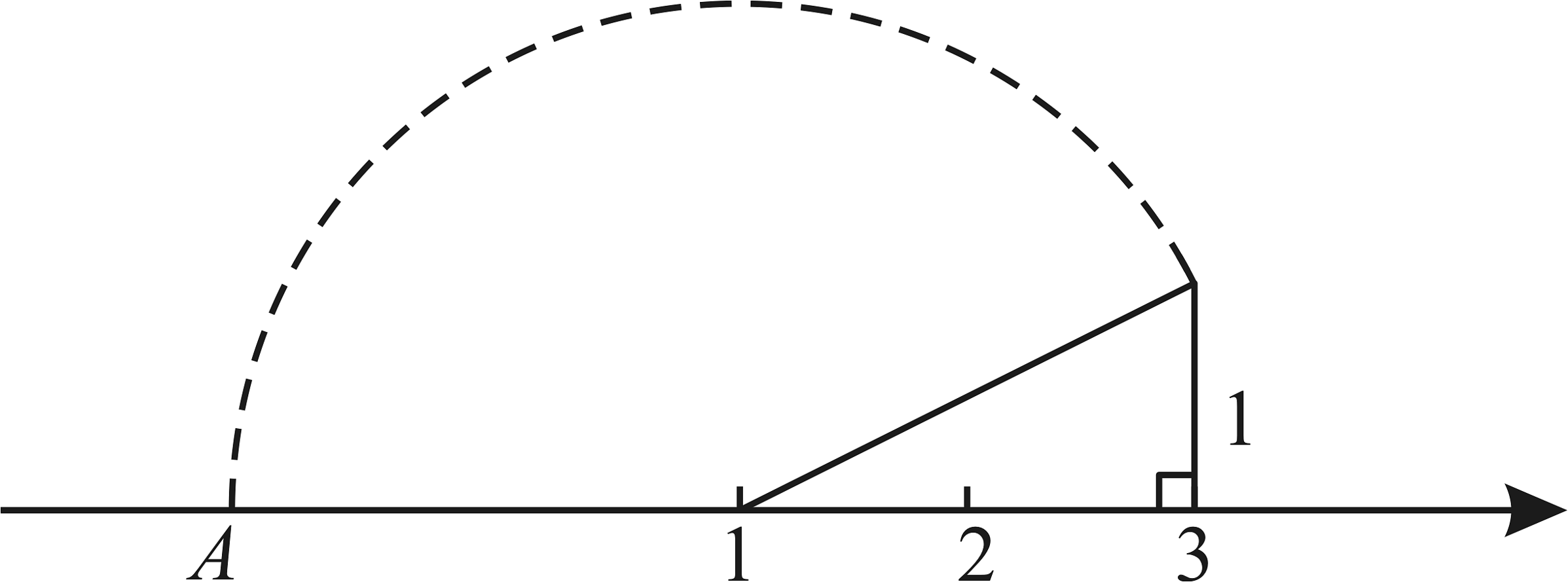 A、 B、 C、 D、4. 如图,在中,在数轴上,以点为圆心,的长为半径画弧,交数轴于点 , 则点表示的数是( )
A、 B、 C、 D、4. 如图,在中,在数轴上,以点为圆心,的长为半径画弧,交数轴于点 , 则点表示的数是( ) A、 B、 C、 D、5. 如图,在中, , . 将AB边与数轴重合,点A,点B对应的数分别为 , 2.以点A为圆心,AC的长为半径画弧,交数轴于点D,则点D表示的数为( )
A、 B、 C、 D、5. 如图,在中, , . 将AB边与数轴重合,点A,点B对应的数分别为 , 2.以点A为圆心,AC的长为半径画弧,交数轴于点D,则点D表示的数为( ) A、3 B、 C、 D、6. 如图,根据尺规作图痕迹,图中标注在点A处所表示的数为( )
A、3 B、 C、 D、6. 如图,根据尺规作图痕迹,图中标注在点A处所表示的数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 如图,数轴上有一个边长为的正方形 , 其中点、表示的数分别为、 , 以为圆心,对角线为半径画弧交数轴上点左边于点 , 则表示的数为 .
 8. 如图1,借助边长为1的正方形,可以准确地将±表示在数轴上。如图2,在数轴上以点A为圆心,边长为1的正方形的对角线长为半径作半圆,该半圆与数轴的右交点为C,与数轴的左交点为B,若点C表示的数是3,则点B表示的数为。
8. 如图1,借助边长为1的正方形,可以准确地将±表示在数轴上。如图2,在数轴上以点A为圆心,边长为1的正方形的对角线长为半径作半圆,该半圆与数轴的右交点为C,与数轴的左交点为B,若点C表示的数是3,则点B表示的数为。 9. 如图,以一个单位长度为边向上作正方形,以表示数1的点为圆心,以正方形对角线为半径作半圆,交数轴于点A,则点A表示的数为
9. 如图,以一个单位长度为边向上作正方形,以表示数1的点为圆心,以正方形对角线为半径作半圆,交数轴于点A,则点A表示的数为 10. 如图,在的方格中,每个小正方形的边长为1.图(1)中正方形ABCD的面积为;如图(2),若点在数轴上表示的数是-1,以为圆心,AD为半径画圆弧与数轴的正半轴交于点 , 则点所表示的数是.
10. 如图,在的方格中,每个小正方形的边长为1.图(1)中正方形ABCD的面积为;如图(2),若点在数轴上表示的数是-1,以为圆心,AD为半径画圆弧与数轴的正半轴交于点 , 则点所表示的数是. 11. 如图,数轴上点对应的数分别为 , 以为边在数轴上方作正方形 , 连接 , 以圆心,的长为半径画圆弧交数轴(的左侧)于 , 则点在数轴上对应的数为 .
11. 如图,数轴上点对应的数分别为 , 以为边在数轴上方作正方形 , 连接 , 以圆心,的长为半径画圆弧交数轴(的左侧)于 , 则点在数轴上对应的数为 . 12. 如图,数轴上A、B、C三点表示的数分别为1, , 2,过点A作直线 , 以点B为圆心,为半径作弧交l于点D,以点A为圆心,线段为半径作弧在点B的左侧交直线于点E,则点E在数轴上表示的数为 .
12. 如图,数轴上A、B、C三点表示的数分别为1, , 2,过点A作直线 , 以点B为圆心,为半径作弧交l于点D,以点A为圆心,线段为半径作弧在点B的左侧交直线于点E,则点E在数轴上表示的数为 .
三、解答题
-
13. 如图,在3×6的方格纸中,每个小方格的边长都为1.请在所给的数轴上画出表示 与的点.(要求:尺规作图,不写作法,保留作图痕迹,写出结论)
 14. 利用圆规和图中数轴上方的正方形网格线,在数轴上表示, 的点。
14. 利用圆规和图中数轴上方的正方形网格线,在数轴上表示, 的点。 15. 在如图所示的4×4 方格中,每个小方格的边长都为 1.
15. 在如图所示的4×4 方格中,每个小方格的边长都为 1. (1)、在图中画出长度为 与 的线段,要求线段的端点在格点上;(2)、在图中画出一个三条边长分别为3, 的三角形,使它的顶点都在格点上.16. 观察图1,每个小正方形的边长均为1.可以得到每个小正方形的面积为1.
(1)、在图中画出长度为 与 的线段,要求线段的端点在格点上;(2)、在图中画出一个三条边长分别为3, 的三角形,使它的顶点都在格点上.16. 观察图1,每个小正方形的边长均为1.可以得到每个小正方形的面积为1.
 (1)、图中阴影正方形的面积为 , 阴影正方形的边长为.(2)、阴影正方形的边长介于两个相邻整数和之间.(3)、利用图1,在数轴上准确地表示出阴影正方形的边长所表示的数以及它的相反数.(4)、请在图2的的方格内作出边长为的正方形.17. 我国著名数学家华罗庚曾说:“数缺形时少直观,形少数时难入微.”数形结合是解决数学问题的重要思想方法.数轴是数形结合的产物,用数轴上的点可以直观地表示实数,从而建立起“数”与“形”之间的联系.
(1)、图中阴影正方形的面积为 , 阴影正方形的边长为.(2)、阴影正方形的边长介于两个相邻整数和之间.(3)、利用图1,在数轴上准确地表示出阴影正方形的边长所表示的数以及它的相反数.(4)、请在图2的的方格内作出边长为的正方形.17. 我国著名数学家华罗庚曾说:“数缺形时少直观,形少数时难入微.”数形结合是解决数学问题的重要思想方法.数轴是数形结合的产物,用数轴上的点可以直观地表示实数,从而建立起“数”与“形”之间的联系. (1)、如图1,点是原点,点对应的实数为 , 过点作垂直于数轴,且 , 连接 , 以为圆心,长为半径画弧,交数轴于点 , 那么点对应的实数为 ;(2)、在(1)的条件下,若将线段向右平移,使得点对应的实数为1,那么此时点对应的实数为 ;(3)、如图2,点对应的实数是3,射线垂直数轴于点 , 请在数轴上作出对应的点 . (要求:尺规作图并保留作图痕迹)
(1)、如图1,点是原点,点对应的实数为 , 过点作垂直于数轴,且 , 连接 , 以为圆心,长为半径画弧,交数轴于点 , 那么点对应的实数为 ;(2)、在(1)的条件下,若将线段向右平移,使得点对应的实数为1,那么此时点对应的实数为 ;(3)、如图2,点对应的实数是3,射线垂直数轴于点 , 请在数轴上作出对应的点 . (要求:尺规作图并保留作图痕迹)