备考2026江苏省中考数学一轮复习（真题实练）：概率和统计
试卷更新日期：2025-10-28 类型：一轮复习
一、选择题
-
1. 一只不透明的袋子中装有4个红球与2个黑球，每个球除颜色外都相同．从中任意摸出3个球，下列事件为必然事件的是（ ）A、至多有1个球是红球 B、至多有1个球是黑球 C、至少有1个球是红球 D、至少有1个球是黑球2. 一只不透明的袋子中，装有3个白球和若干个红球，这些球除颜色外都相同，搅匀后从中任意摸出一个球，摸到白球的概率为 则红球的个数为（ ）A、1 B、2 C、3 D、43. 下列说法不正确的是（ ）A、明天下雨是随机事件 B、调查长江中现有鱼的种类，适宜采用普查的方式 C、描述一周内每天最高气温的变化情况，适宜采用折线统计图 D、若甲组数据的方差S甲2＝0.13，乙组数据的方差S乙2＝0.04，则乙组数据更稳定4. 一组数据：13，14，14，16，18，这组数据的平均数和众数分别是（ ）A、15，14 B、14，15 C、14，14 D、15，15
二、填空题
-
5. 某篮球队在一次联赛中共进行了6场比赛，得分依次为：71，71，65，71，64，66.这组数据的众数为.6. 一组数据6，8，10，x的平均数是9，则x的值为 ．7. 小丽6次射击的成绩如图所示，则她的射击成绩的中位数为 环．
8. 小明家1～5月的电费（单位：元）分别为：137，140，140，117，104．该组数据的中位数是 ．9. 某公司在一次招聘中，分笔试和面试两部分，笔试和面试成绩按计算最终成绩．小李的笔试成绩为85分，面试成绩为90分，则小李的最终成绩为分．三、解答题
-
10. 如图，甲、乙为两个可以自由转动的转盘，它们分别被分成了4等份与3等份，每份内均标有字母，转盘停止转动后，若指针落在两个区域的交线上，则重转一次．
(1)、转动甲盘，待其停止转动后，指针落在A区域的概率为 ；(2)、转动甲、乙两个转盘，用列表或画树状图的方法，求转盘停止转动后甲盘指针落在C区域且乙盘指针未落在Q区域的概率．11. 为了解某景区外地自驾游客的分布情况，某日小桐随机调查了该景区附近部分宾馆停车场的车辆数，根据车牌号归属地的不同，绘制了如图统计图（不完整）：
根据图中信息，解答下列问题．
(1)、小桐共调查了 辆车，“豫”对应扇形的圆心角为 °；(2)、补全条形统计图；(3)、若该景区附近宾馆停车场当日共有450辆外地自驾游客的车辆，估计其中车牌号归属地为“皖”的车辆有多少？12. 为继承和弘扬中华优秀传统文化，某校将八年级学生随机安排到以下四个场所参加社会实践活动．
已知小明、小华、小丽都是该校八年级学生，求下列事件的概率：
(1)、小明到南通博物苑参加社会实践活动；(2)、小华和小丽都到南通美术馆参加社会实践活动．13. 为提升学生体质健康水平，促进学生全面发展，某校大课间共开展6项体育活动，每名学生均参加了其中一项活动．为了解该校学生参与大课间体育活动情况，随机抽取了该校50名学生进行调查，得到如下未完成的统计表．体育活动
足球
篮球
排球
乒乓球
跳绳
啦啦操
人数
6
a
10
9
8
5
(1)、表格中a的值为 ；(2)、若该校有1000名学生，请估计该校参加足球活动的学生人数；(3)、为备战校际篮球联赛，学校计划从参加篮球活动的甲、乙两名同学中选拔一人加入校篮球队．已知甲、乙两名同学近六周定点投篮测试成绩（每次测试共有10次投篮机会，以命中次数作为测试成绩）如图所示．你建议选拔哪名同学，请说明理由．14. 2025年1月14日，教育部办公厅印发了《中小学科学教育工作指南》（以下简称《指南》），旨在推动中小学科学教育更加重视激发学生好奇心、想象力、探求欲，培育具备科学家潜质、愿意献身科学研究事业的青少年群体．某校为落实《指南》要求，准备在七年级开设“3D打印”“航模”“机器人”“无人机”共四类科技社团（每名学生必选且仅选一个社团）．为了解学生参加各社团的意向，现随机抽取七年级部分学生进行问卷调查，并对问卷数据进行收集、整理、描述和分析，部分信息如下：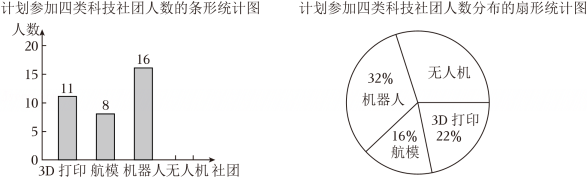
请根据以上信息，解答下列问题：
(1)、本次调查的样本容量为 ▲ ，并将条形统计图补充完整；（画图后请标注相应的数据）(2)、若该校七年级共有1000名学生，请估计计划参加“机器人”社团的学生人数；(3)、根据上述统计分析情况，请你为该校科技社团活动的顺利开展给出一条合理建议．15. 一只不透明的袋子中装有标号分别为1，2，3，4的4个球，这些球除标号外都相同．(1)、将球搅匀，从中任意摸出1个球，摸到标号为2的球的概率是 ；(2)、将球搅匀，从中任意摸出1个球，记录标号后不放回，再从袋子中任意摸出1个球，记录标号．求两次摸到的球标号均小于3的概率．（请用“画树状图”或“列表”等方法写出分析过程）16. 某校建议学生利用周末时间积极参加社会实践活动．某一周末有两个项目供学生选择：A文明交通劝导志愿行，B乡村教育关爱行，每名学生只能选择其中一个项目．(1)、甲同学选择A项目的概率为；(2)、请用画树状图的方法，求甲、乙、丙三位同学恰好选择同一项目的概率．17. 2025年2月，江苏省教育厅印发《关于在义务教育学校实施“2・15专项行动”的通知》，明确提出“中小学生每天综合体育活动时间不低于2小时”．某校采取多种举措，确保学生每天有充足的体育活动时间，同时监测学生的体质健康情况．为此，学校从全体男生中随机抽取部分学生调查他们的立定跳远成绩，并把成绩分成五档（A档、B档、C档、D档、E档 ， 单位：），绘制成统计图．其中部分数据丢失，请结合统计图，完成下列问题：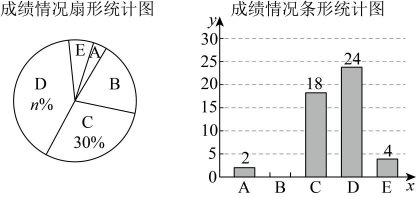
(1)、扇形统计图中的值为 ， 条形统计图中“B档”成绩的人数为；(2)、本次抽测中，立定跳远成绩的中位数落在档；(3)、若该校共有1200名男生，请你估计该校立定跳远成绩为“E档”的男生人数．18. 在5张相同的小纸条上，分别写有：①-1；②0；③1；④正数；⑤负数将这5张小纸条做成5支签，①、②、③放在不透明的盒子A中搅匀，④、⑤放在不透明的盒子B中搅匀.(1)、从盒子A中任意抽出1支签，抽到0的概率是.(2)、先从盒子A中任意抽出1支签，再从盒子B中任意抽出1支签.求抽到的数与文字描述相符合的概率.19. 甲、乙两人在相同条件下10次射击的成绩如下：人员
环数
甲
6
7
6
8
7
6
8
6
9
7
乙
5
7
5
10
5
8
9
9
8
7
对以上数据进行分析，绘制成下表：
人员
平均数
中位数
众数
方差：
甲
7
m
1
乙
7
n
5
2.8
(1)、填空：= ， m= ， n=.(2)、根据以上数据，评价甲、乙两人射击成绩的稳定性，并说明理由。20. 随着人工智能的快速发展，初中生使用AI大模型辅助学习快速普及，并呈现出多样化趋势.某研究性学习小组采用简单随机抽样的方法，对本校九年级学生一周使用AI大模型辅助学习的时间（用x表示，单位：min）进行了抽样调查.把所得的数据分组整理，并绘制成频数分布直方图：抽取的学生一周使用AI大模型
辅助学习时间频率分布表
组别
时间x（min）
频率
A
0.16
B
0.24
C
0.30
D
0.20
E
0.10
合计
1
抽取的学生一周使用 AI大模型
根据提供的信息回答问题：
(1)、请把频数分布直方图补充完整（画图后标注相应数据）；(2)、调查所得数据的中位数落在组（填组别）；(3)、该校九年级共有750名学生，根据抽样调查结果，估计该校九年级学生一周使用AI大模型辅助学习的时间不少于60 min的学生人数.21. 为了弘扬社会主义核心价值观，学校决定组织“立鸿鹄之志，做有为少年”主题观影活动，建议同学们利用周末时间自主观看.现有 A，B，C共3部电影，甲、乙2位同学分别从中任意选择1部电影观看.(1)、甲同学选择 A 电影的概率为；(2)、求甲、乙2位同学选择不同电影的概率.（请用画树状图或列表等方法说明理由）22. 一只不透明的袋子中装有1个红球和3个白球，这些球除颜色外都相同，(1)、搅匀后从中任意摸出1个球，则摸到红球的概率是；(2)、搅匀后从中任意摸出1个球，记录颜色后放回、搅匀，再从中任意摸出1个球.用画树状图或列表的方法，求2次都摸到白球的概率23. 为了解八年级学生的体重情况，某校随机抽取了八年级部分学生进行测量，收集并整理数据后，绘制了如下尚不完整的统计图表体重情况统计表
组别
体重x（kg）
频数（人数）
A类
x＜49.5
10
B类
49.5≤x<59.5
a
C类
59.5≤x<69.5
8
D类
x≥69.5
b
根据以上信息，解答下列问题：
(1)、a= ， b=；(2)、在扇形统计图中，C类所对应的圆心角度数是°；(3)、若该校八年级共有1200名学生，估计体重在59.5kg及以上的学生有多少人?24. 为打造活力校园，某校在大课间开展了丰富多彩的活动，现有4种体育类活动供学生选择：A ． 羽毛球，B ． 乒乓球，C ． 花样跳绳，D ． 踢毽子，每名学生只能选择其中一种体育活动．(1)、若小明在这4种体育活动中随机选择，则选中“乒乓球”的概率是 ；(2)、请用画树状图或列表的方法，求小明和小聪随机选择选到同一种体育活动的概率．25. 为角逐市校园“音乐达人”大赛，小红和小丽参加了校内选拔赛，10位评委的评分情况如下（单位：分）．表1评委评分数据
选手
评委评分
小红
7
8
7
8
7
7
7
8
7
9
小丽
7
7
6
8
8
8
8
8
7
8
表2评委评分数据分析
选手
平均数
中位数
众数
小红
7.5
b
7
小丽
a
8
c
根据以上信息，回答下列问题：
(1)、表2中a＝ ，b＝ ，c＝ ；(2)、你认为小红和小丽谁的成绩较好？请说明理由．26. 参加初中学业水平考试的人数简称“中考人数”．如图，某市根据2016﹣2024年中考人数及2024年上半年小学、初中各年级在校学生人数，绘制出2016﹣2032年中考人数（含预估）统计图如图：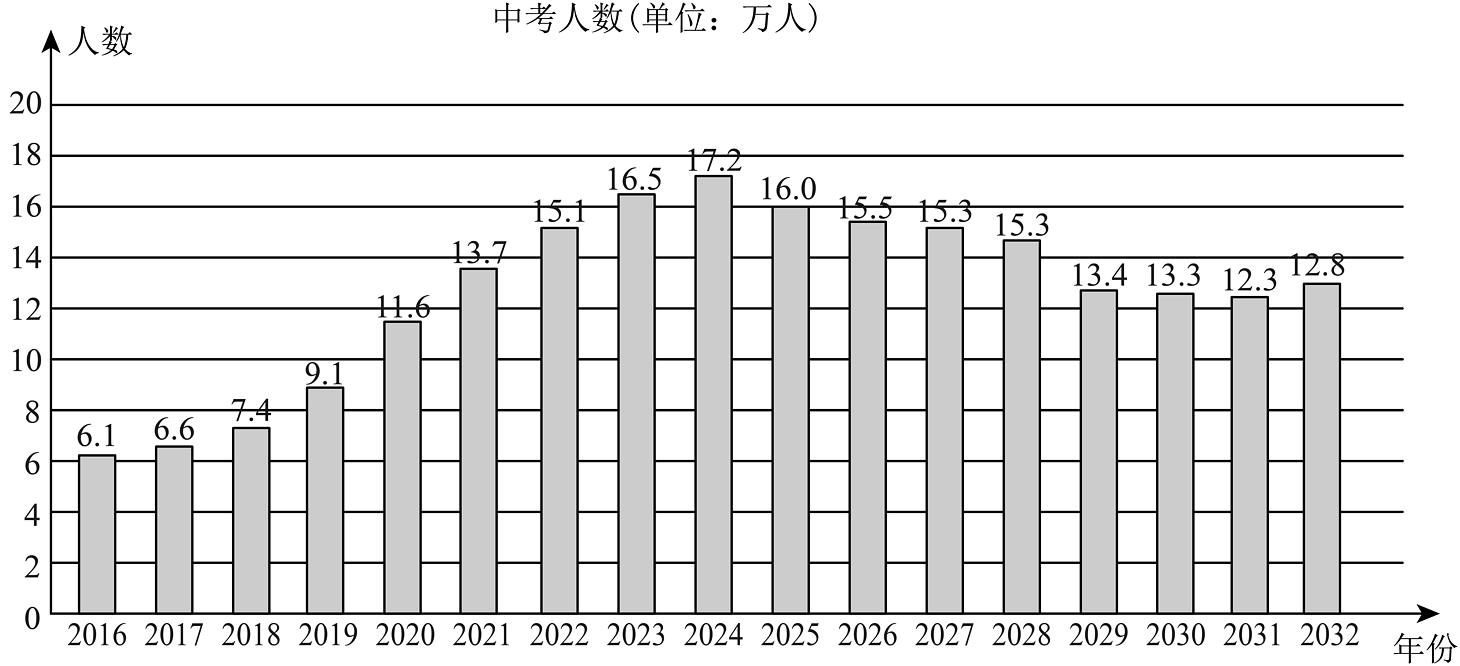
根据以上信息，解决下列问题．
(1)、下列结论中，所有正确结论的序号是______．①2016﹣2031年中考人数呈现先升后降的趋势；
②与上一年相比，中考人数增加最多的年份是2021年；
③2016﹣2024年中考人数的波动比2024﹣2032年中考人数的波动大．
(2)、为促进人口长期均衡发展，有效提高人口出生率，我国于2013﹣2021年先后实施了三项鼓励生育的政策，其中导致该市2032年中考人数较2031年增加的最主要原因是______．A.2013年单独两孩政策
B.2015年全面两孩政策
C.2021年三孩生育政策
(3)、2024年上半年，该市小学在校学生共有多少人？27. 不透明的袋子中装有2个红球与2个白球，这些球除颜色外无其他差别．(1)、甲从袋子中随机摸出1个球，摸到红球的概率为______；(2)、甲、乙两人分别从袋子中随机摸出1个球（不放回），用列表或画树状图的方法，求两人摸到相同颜色球的概率．28. 南通地铁1号线“世纪大道站”有标识为1、2、3、4的四个出入口．某周六上午，甲、乙两位学生志愿者随机选择该站一个出入口，开展志愿服务活动．(1)、甲在2号出入口开展志愿服务活动的概率为 ；(2)、求甲、乙两人在同一出入口开展志愿服务活动的概率．29. 我国淡水资源相对缺乏，节约用水应成为人们的共识．为了解某小区家庭用水情况，随机调查了该小区50个家庭去年的月均用水量（单位：吨），绘制出如下未完成的统计图表．50个家庭去年月均用水量频数分布表
组别
家庭月均用水量（单位：吨）
频数
A
2.0≤t＜3.4
7
B
3.4≤t＜4.8
m
C
4.8≤t＜6.2
n
D
6.2≤t＜7.6
6
E
7.6≤t＜9.0
2
合计
50
根据上述信息，解答下列问题：
(1)、m＝ ， n＝；(2)、这50个家庭去年月均用水量的中位数落在 组；(3)、若该小区有1200个家庭，估计去年月均用水量小于4.8吨的家庭数有多少个？
30. 3张相同的卡片上分别写有中国二十四节气中的“小满”、“芒种”、“夏至”的字样，将卡片的背面朝上．(1)、洗匀后，从中任意抽取1张卡片，抽到写有“小满”的卡片的概率等于；(2)、洗匀后，从中任意抽取2张卡片，用画树状图或列表的方法，求抽到一张写有“芒种”，一张写有“夏至”的卡片的概率．31. 有甲、乙两只不透明的袋子，每只袋子中装有红球和黄球若干，各袋中所装球的总个数相同，这些球除颜色外都相同．实践组用甲袋、创新组用乙袋各自做摸球试验：两人一组，一人从袋中任意摸出1个球，另一人记下颜色后将球放回并搅匀，各组连续做这样的试验，将记录的数据绘制成如下两种条形统计图：
(1)、图能更好地反映各组试验的总次数，图能更好地反映各组试验摸到红球的频数（填“A”或“B”）；(2)、求实践组摸到黄球的频率；(3)、根据以上两种条形统计图，你还能获得哪些信息（写出一条即可）？32. 某校为丰富学生的课余生活，开展了多姿多彩的体育活动，开设了五种球类运动项目：A篮球，B足球，C排球，D羽毛球，E乒乓球．为了解学生最喜欢以上哪种球类运动项目，随机抽取部分学生进行调查（每位学生仅选一种），并绘制了统计图．某同学不小心将图中部分数据丢失，请结合统计图，完成下列问题：
(1)、本次调查的样本容量是 ， 扇形统计图中C对应圆心角的度数为°；(2)、请补全条形统计图；(3)、若该校共有2000名学生，请你估计该校最喜欢“E乒乓球”的学生人数．33. 一只不透明的袋子中装有1个白球、1个红球和1个绿球，这些球除颜色外都相同．(1)、将球搅匀，从中任意摸出1个球，摸到白球的概率是；(2)、将球搅匀，从中任意摸出1个球，记录颜色后放回、搅匀，再从中任意摸出1个球．求2次摸到的球颜色不同的概率．（请用“画树状图”或“列表”等方法写出分析过程）