备考2026江苏省中考数学一轮复习（真题实练）：图形的运动及三角函数

试卷更新日期：2025-10-28 类型：一轮复习

进入出卷网下载

一、选择题

1. 传统纹样作为中华传统文化的一部分，具有深厚的底蕴．徐州出土汉代玉器的下列纹样，既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 小明的背包随安检传送带移动，主要涉及的图形变换是（　　）

A、平移 B、轴对称 C、旋转 D、位似

查看试题解析
3. 下列图形中，为三棱柱的侧面展开图的是（）

A、 B、 C、 D、

查看试题解析
4. 某几何体的三视图如图所示，这个几何体是（）

A、圆柱 B、圆锥 C、正方体 D、长方体

查看试题解析
5. 窗棂是中国传统木构建筑的重要元素，既散发着古典之韵，又展现了几何之美．下列窗棂图案中，是轴对称图形但不是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
6. 如图，在△ABC中，∠B＝80°，∠C＝65°，将△ABC绕点A逆时针旋转得到△AB^'C^' ．当AB^'落在AC上时，∠BAC^'的度数为（）

A、65° B、70° C、80° D、85°

查看试题解析
7. 在△ABC中，∠C＝90°，tanA $= \frac{1}{2}$ ， AC＝2 $\sqrt{5}$ ，则BC的长为（　　）

A、1 B、2 C、 $\sqrt{5}$ D、5

查看试题解析
8. 如图为一个正方体的展开图，将其折成一个正方体，所得图形可能是（　　）

A、 B、 C、 D、

查看试题解析
9. 如图是一个几何体的三视图（图中尺寸单位：cm），则这个几何体的底面圆的周长为（　　）

A、6πcm B、9πcm C、12πcm D、16πcm

查看试题解析
10. 如图，将△ABC沿着射线BC平移到△DEF．若BC＝6，EC＝4，则平移的距离为（　　）

A、2 B、4 C、6 D、8

查看试题解析
11. 如图，在Rt△ABC中， $∠ A = 9 0^{°}$ ， $A B = 3$ ， $A C = 4$ ，则sinB的值是（）

A、 $\frac{3}{5}$ B、 $\frac{3}{4}$ C、 $\frac{4}{5}$ D、 $\frac{4}{3}$

查看试题解析
12. 如图，在 $△ A B C$ 中， $∠ A C B = 9 0^{°}$ ， $∠ C A B = 3 0^{°}$ ， AD平分 $∠ C A B$ ， $B E ⊥ A D$ ， E为垂足，则 $\frac{A D}{B E}$ 的值为（）

A、 $2 \sqrt{3}$ B、 $\frac{7 \sqrt{3}}{3}$ C、 $\frac{5}{2} \sqrt{3}$ D、 $\frac{8 \sqrt{3}}{3}$

查看试题解析
13. 如图1，在菱形 $A B C D$ 中， $∠ A B C = 60 °$ ，连接 $B D$ ，点M从B出发沿 $B D$ 方向以 $\sqrt{3} cm/s$ 的速度运动至D，同时点N从B出发沿 $B C$ 方向以 $1 cm / s$ 的速度运动至C，设运动时间为 $x (s)$ ， $△ B M N$ 的面积为 $y ({cm}^{2})$ ， y与x的函数图象如图2所示，则菱形 $A B C D$ 的边长为（）

A、 $2 \sqrt{2} cm$ B、 $4 \sqrt{2} cm$ C、 $4 cm$ D、 $8 cm$

查看试题解析
14. 如图，在菱形ABCD中，∠ABC＝60°，E是CD的中点，则sin∠EBC的值为（）

A、 $\frac{\sqrt{3}}{5}$ B、 $\frac{\sqrt{7}}{5}$ C、 $\frac{\sqrt{21}}{14}$ D、 $\frac{5 \sqrt{7}}{14}$

查看试题解析
15. 如图，在正方形 ABC'D中，E 为边AD 的中点，连接BE，将△ABE沿BE 翻折，得到△A'BE，连接A'C. A'D，则下列结论不正确的是（）

A、A'D ∥BE B、 $A^{'} C = \sqrt{2} A^{'} D$ C、△A'CD 的面积=△A'DE的面积 D、四边形A'BED 的面积=△A'BC的面积

查看试题解析

二、填空题

16. 社团活动课上，九年级学习小组测量学校旗杆的高度．如图，他们在B处测得旗杆顶部A的仰角为60°，BC＝6m ，则旗杆AC的高度为 m ．

查看试题解析
17. 如图，网格图中每个小正方形的面积都为1．经过网格点A的一条直线，把网格图分成了两个部分，其中△BMN的面积为3，则sin∠MNB的值为．

查看试题解析
18. 如图，一块砖的A，B，C三个面的面积比是5：3：1．如果B面向下放在地上，地面所受压强为a Pa，那么C面向下放在地上时，地面所受压强为 Pa．

查看试题解析
19. 如图，在△ABC中，tanC= $\frac{1}{3}$ ， D是边BC上一点，将△ACD沿AD翻折得到△AED使线段AE、BC相交于点F若CF=5，EF=2，则AC=.

查看试题解析
20. 围棋起源于中国，古代称为“弈”．如图是两位同学的部分对弈图，轮到白方落子，观察棋盘，白方如果落子于点的位置，则所得的对弈图是轴对称图形．（填写A，B，C，D中的一处即可，A，B，C，D位于棋盘的格点上）

查看试题解析
21. 物理课上学过小孔成像的原理，它是一种利用光的直线传播特性实现图像投影的方法．如图，燃烧的蜡烛 $($ 竖直放置 $) A B$ 经小孔 $O$ 在屏幕 $($ 竖直放置 $)$ 上成像 $A' B' .$ 设 $A B = 36 c m$ ， $A' B' = 24 c m .$ 小孔 $O$ 到 $A B$ 的距离为 $30 c m$ ，则小孔 $O$ 到 $A' B'$ 的距离为 $c m$ ．

查看试题解析
22. 如图，小明用无人机测量教学楼的高度，将无人机垂直上升距地面30m的点P处，测得教学楼底端点A的俯角为37°，再将无人机沿教学楼方向水平飞行26.6m至点Q处，测得教学楼顶端点B的俯角为45°，则教学楼AB的高度约为 m．（精确到1m，参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

查看试题解析
23. 如图，在△ABC中，AC＝2，AB＝3，直线CM∥AB ， E是BC上的动点（端点除外），射线AE交CM于点D ．在射线AE上取一点P ，使得AP＝2ED ，作PQ∥AB ，交射线AC于点Q ．设AQ＝x ， PQ＝y ．当x＝y时，CD＝；在点E运动的过程中，y关于x的函数表达式为．

查看试题解析

三、解答题

24. 下圆墩是“彭城七里”的起点，也是徐州城市历史的源头．某校数学综合与实践小组到下圆墩遗址公园参观，发现一处三角形的景观墙（如图），记作△ABC，同学们测得BC＝22.2m，∠B＝34.2°，∠C＝9.8°，求AC的长度．（精确到0.1m，参考数据：sin34.2°≈0.56，cos34.2°≈0.83，tan34.2°≈0.68，sin9.8°≈0.17，cos9.8°≈0.99，tan9.8°≈0.17）

查看试题解析
25. 小明和小军两位同学对某河流的宽度进行测量，如图所示，两人分别站在同侧河岸上的点 $A$ 、 $B$ 处，选取河对岸的一块石头 $C$ 作为测量点（点 $A 、 B 、 C$ 在同一水平面内），小明同学在点 $A$ 处测得 $∠ B A C$ 为 $42 °$ ，小军同学在点 $B$ 处测得 $∠ A B C$ 为 $61 °$ ，两人之间的距离 $A B$ 为60米，求此河流的宽度．（参考数据： $s i n 42 ° \approx 0.67, t a n 42 ° \approx 0.90, s i n 61 ° \approx 0.87, t a n 61 ° \approx 1.80$ ）

查看试题解析
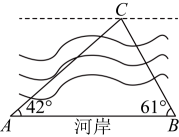26. 如图，港口B位于岛A的北偏西 $3 7^{°}$ 方向，灯塔C在岛A的正东方向， $A C = 6 k m$ ，一艘海轮D在岛A的正北方向，且B、D、C三点在一条直线上， $D C = \frac{5}{2} B D$ .

(1)、求岛A与港口B之间的距离；

(2)、求tanC.（参考数据： $s i n 3 7^{°} \approx \frac{3}{5}$ ， $c o s 3 7^{°} \approx \frac{4}{5}$ ， $t a n 3 7^{°} \approx \frac{3}{4}$ ）

查看试题解析
27. 如图，在徐州云龙湖旅游景区，点 $A$ 为“彭城风华”观演场地，点 $B$ 为“水族展览馆”，点 $C$ 为“徐州汉画像石艺术馆”．已知 $∠ B A C = 60 °$ ， $∠ B C A = 45 °$ ， $A C = 1640 m$ ．求“彭城风华”观演场地与“水族展览馆”之间的距离 $A B$ （精确到 $1 m$ ）．（参考数据： $\sqrt{2} \approx 1.41$ ， $\sqrt{3} \approx 1.73$ ）

查看试题解析
28. 图①是某种可调节支撑架，BC为水平固定杆，竖直固定杆 $A B ⊥ B C$ ，活动杆AD可绕点A旋转，CD为液压可伸缩支撑杆，已知 $A B = 10 c m$ ， $B C = 20 c m$ ， $A D = 50 c m$ ．

(1)、如图②，当活动杆AD处于水平状态时，求可伸缩支撑杆CD的长度（结果保留根号）；

(2)、如图③，当活动杆AD绕点A由水平状态按逆时针方向旋转角度 $α$ ，且 $t a n α = \frac{3}{4}$ （ $α$ 为锐角），求此时可伸缩支撑杆CD的长度（结果保留根号）．

查看试题解析
29. 两个智能机器人在如图所示的 $R t △ A B C$ 区域工作， $∠ A B C = 9 0^{\circ}, A B = 40 m, B C = 30 m,$ 直线 BD 为生产流水线，且BD 平分 $△ A B C$ 的面积（即D为AC 中点）.机器人甲从点A 出发，沿A→B的方向以 $v_{1} (m / m i n)$ 的速度匀速运动，其所在位置用点 P 表示，机器人乙从点 B 出发，沿B→C→D的方向以 $v_{2} (m / m i n)$ 的速度匀速运动，其所在位置用点 Q 表示.两个机器人同时出发，设机器人运动的时间为t（min），记点P到 BD 的距离（即垂线段 $P P^{'}$ 的长）为 $d_{1} (m),$ 点Q到 BD的距离（即垂线段（ $Q Q^{'}$ 的长）为 $d_{2} (m) .$ .当机器人乙到达终点时，两个机器人立即同时停止运动，此时 $d_{1} = 7.5 m . d_{2}$ 与t的部分对应数值如下表 $（ t_{1} ＜ t_{2} ）;$
t（min）
0
$t_{1}$
$t_{2}$
5.5
$d_{2} (m)$
0
16
16
0

(1)、机器人乙运动的路线长为m；

(2)、求 $t_{2} - t_{1}$ 的值；

(3)、当机器人甲、乙到生产流水线 BD 的距离相等（即 $d_{1} = d_{2} ）$ 时，求t 的值.

查看试题解析
30. 如图，在▱ $A B C D$ 中， $A B = 6$ ， $A D = 10$ ， $∠ B A D = 60 °$ ， $P$ 为边 $A B$ 上的动点．连接 $P C$ ，将 $P C$ 绕点 $P$ 逆时针旋转 $60 °$ 得到 $P E$ ，过点 $E$ 作 $E F ∥ A B$ ， $E F$ 交直线 $A D$ 于点 $F$ ．连接 $P F$ 、 $D E$ ，分别取 $P F$ 、 $D E$ 的中点 $M$ 、 $N$ ，连接 $M N$ ，交 $A D$ 于点 $Q$ ．

(1)、若点 $P$ 与点 $B$ 重合，则线段 $M N$ 的长度为______．

(2)、随着点 $P$ 的运动， $M N$ 与 $A Q$ 的长度是否发生变化？若不变，求出 $M N$ 与 $A Q$ 的长度；若改变，请说明理由．

查看试题解析
31. 如图，已知 $∠ P A Q$ 及 $A P$ 边上一点 $C$ ．

(1)、用无刻度直尺和圆规在射线 $A Q$ 上求作点 $O$ ，使得 $∠ C O Q = 2 ∠ C A Q$ ； $($ 保留作图痕迹，不写作法 $)$

(2)、在 $(1)$ 的条件下，以点 $O$ 为圆心，以 $O A$ 为半径的圆交射线 $A Q$ 于点 $B$ ，用无刻度直尺和圆规在射线 $C P$ 上求作点 $M$ ，使点 $M$ 到点 $C$ 的距离与点 $M$ 到射线 $A Q$ 的距离相等； $($ 保留作图痕迹，不写作法 $)$

(3)、在 $(1)$ 、 $(2)$ 的条件下，若 $s i n A = \frac{3}{5}$ ， $C M = 12$ ，求 $B M$ 的长．

查看试题解析

四、实践探究题

32. 某校数学研究性学习小组为测量物体的高度，开展了如下综合与实践活动．
【活动主题】测量物体的高度
【测量工具】卷尺、标杆
【活动过程】
活动1：测量校内旗杆的高度
该小组在校内进行了旗杆高度的测量活动（示意图1）．在点F处竖立标杆EF ，直立在点Q处的小军从点P处看到标杆顶E、旗杆顶M在同一条直线上．已知旗杆底端N与F、Q在同一条直线上，EF＝2.8m ， PQ＝1.4m ， QF＝2m ， FN＝16m ．

(1)、求旗杆MN的高度．

(2)、活动2：测量南禅寺妙光塔的高度
南禅寺妙光塔，简称“妙光塔”，始建于北宋雍熙年间，是无锡著名的文物保护单位之一．该小组为全面了解本土历史文物，决定走出校园去测量妙光塔的高度．他们到达妙光塔后，发现塔顶A和塔底中心B均无法到达．经研究，设计并实施了如下测量活动（示意图2）．在地面一条水平步道上的点F处竖立标杆EF ，直立在点Q处的小军从点P处看到标杆顶E、塔顶A在同一条直线上．小军沿FQ的方向走到点Q^'处，此时标杆E^'F^'竖立于F^'处，从点P^'处看到标杆顶E^'、塔顶A在同一条直线上．已知AB、EF、PQ、E^'F^'和P^'Q^'在同一平面内，点B、F、Q、F^'、Q^'在同一条直线上，EF＝E^'F^'＝2.8m ， PQ＝P^'Q^'＝1.4m ， FQ＝1.2m ， F^'Q^'＝2.2m ， QQ^'＝30m ．
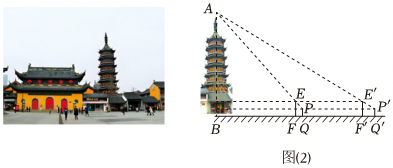
求妙光塔AB的高度．

查看试题解析
33. 综合与实践
小明同学用一副三角板进行自主探究.如图， $△ A B C$ 中， $A C B = 9 0^{\circ}, C A = C B, △ C D E$ 中， $∠ D C E = 9 0^{\circ}, ∠ E = 3 0^{\circ}, A B = C E = 12 c m .$

(1)、【观察感知】
如图①，将这副三角板的直角顶点和两条直角边分别重合，AB，DE 交于点 F，求 $∠ A F D$ 的度数和线段AD 的长.（结果保留根号）

(2)、【探索发现】
在图①的基础上，保持 $△ C D E$ 不动，把 $△ A B C$ 绕点C按逆时针方向旋转一定的角度，使得点 A 落在边 DE 上（如图 ②）.
①求线段AD 的长；（结果保留根号）
②判断AB 与DE 的位置关系，并说明理由.

查看试题解析

34. 双塔是古黄河宿迁景观带的标志性建筑之一，由九层的九龙塔和七层的七风塔构成．某校数学实践小组开展测量七凤塔高度的实践活动，该小组制定了测量方案，在实地测量后撰写活动报告，报告部分内容如表：

测量七凤塔高度
测量工具	测角仪、皮尺等	活动形式	以小组为单位
测量示意图		测量步骤及结果
		如图，步骤如下： ①在C处使用测角仪测得塔的顶部点B的仰角∠BDG=37°； ②沿着CA方向走到E处，用皮尺测得CE＝24米； ③在E处使用测角仪测得塔的顶部点B的仰角∠BFG＝45°.
……

已知测角仪的高度为1.2米，点C、E、A在同一水平直线上．根据以上信息，求塔AB的高度．

（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

查看试题解析

35. 图1、2是一个折叠梯的实物图．图3是折叠梯展开、折叠过程中的一个主视图．图4是折叠梯充分展开后的主视图，此时点E落在AC上，已知AB＝AC ， sin $∠ B A C \approx \frac{4}{5}$ ，点D、F、G、J在AB上，DE、FM、GH、JK均与BC所在直线平行，DE＝FM＝GH＝JK＝20cm ， DF＝FG＝GJ＝30cm ．点N在AC上，AN、MN的长度固定不变．图5是折叠梯完全折叠时的主视图，此时AB、AC重合，点E、M、H、N、K、C在AB上的位置如图所示．

(1)、【分析问题】
如图5，用图中的线段填空：AN＝MN+EM+AD﹣；

(2)、如图4，sin∠MEN≈ ，由 AN＝EN+AE＝EN+AD ，且AN的长度不变，可得MN与EN之间的数量关系为；

(3)、【解决问题】
求MN的长．

查看试题解析

五、阅读理解题

36. 主题学习：仅用一把无刻度的直尺作图
【阅读理解】
任务：如图1，点D、E分别在△ABC的边AB、AC上，DE∥BC ，仅用一把无刻度的直尺作DE、BC的中点．
操作：如图2，连接BE、CD交于点P ，连接AP交DE于点M ，延长AP交BC于点N ，则M、N分别为DE、BC的中点．
理由：由DE∥BC可得△ADM∽△ABN及△AEM∽△ACN ，所以 $\frac{D M}{B N} = \frac{A M}{A N}$ ， $\frac{E M}{C N} = \frac{A M}{A N}$ ，所以 $\frac{D M}{E M} = \frac{B N}{C N}$ ，同理，由△DMP∽△CNP及△EMP∽△BNP ，可得 $\frac{D M}{C N} = \frac{M P}{N P}$ ， $\frac{E M}{B N} = \frac{M P}{N P}$ ，所以 $\frac{D M}{E M} = \frac{C N}{B N}$ ，所以 $\frac{B N}{C N} = \frac{C N}{B N}$ ，则BN＝CN ， DM＝EM ，即M、N分别为DE、BC的中点．
【实践操作】
请仅用一把无刻度的直尺完成下列作图，要求：不写作法，保留作图痕迹．

(1)、如图3，l₁∥l₂ ，点E、F在直线l₂上．
①作线段EF的中点；
②在①中作图的基础上，在直线l₂上位于点F的右侧作一点P ，使得PF＝EF；

(2)、小明发现，如果重复上面的过程，就可以作出长度是已知线段长度的3倍、4倍、…、k倍（k为正整数）的线段．如图4，l₁∥l₂ ，已知点P₁、P₂在l₁上，他利用上述方法作出了P₂P₃＝P₃P₄＝P₁P₂.点E、F在直线l₂上，请在图4中作出线段EF的三等分点；

(3)、【探索发现】
请仅用一把无刻度的直尺完成作图，要求：不写作法，保留作图痕迹．
如图5，DE是△ABC的中位线．请在线段EC上作出一点Q ，使得QE $= \frac{1}{3}$ CE（要求用两种方法）．

查看试题解析

六、综合题

37. 如图，点 $A 、 B 、 M 、 E 、 F$ 依次在直线 $l$ 上，点 $A 、 B$ 固定不动，且 $A B = 2$ ，分别以 $A B 、 E F$ 为边在直线 $l$ 同侧作正方形 $A B C D$ 、正方形 $E F G H$ ， $∠ P M N = 90^{\circ}$ ，直角边 $M P$ 恒过点 $C$ ，直角边 $M N$ 恒过点 $H$ ．

(1)、如图 $1$ ，若 $B E = 10$ ， $E F = 12$ ，求点 $M$ 与点 $B$ 之间的距离；

(2)、如图 $1$ ，若 $B E = 10$ ，当点 $M$ 在点 $B 、 E$ 之间运动时，求 $H E$ 的最大值；

(3)、如图 $2$ ，若 $B F = 22$ ，当点 $E$ 在点 $B 、 F$ 之间运动时，点 $M$ 随之运动，连接 $C H$ ，点 $O$ 是 $C H$ 的中点，连接 $H B 、 M O$ ，则 $2 O M + H B$ 的最小值为．

查看试题解析

t（min）	0	$t_{1}$	$t_{2}$	5.5
$d_{2} (m)$	0	16	16	0