备考2026江苏省中考数学一轮复习（真题实练）：圆
试卷更新日期：2025-10-28 类型：一轮复习
一、选择题
-
1. 已知圆锥的底面圆半径为3，母线长为4，则圆锥的侧面积为（ ）A、6π B、12π C、15π D、24π2. 已知圆弧所在圆的半径为6，该弧所对的圆心角为90°，则这条弧的长为（ ）A、2π B、3π C、4π D、6π3. 如图，的半径为2，直径AB，CD互相垂直，则弧的长是（ ）
A、 B、 C、 D、4. 如图，将一枚飞镖任意投掷到正方形镖盘内，若飞锤落在镖盘内各点的机会相等，则飞镖落在阴影区域的概率为（ ）
A、 B、 C、 D、二、填空题
-
5. “苏州之眼”摩天轮是亚洲最大的水上摩天轮，共设有28个回转式太空舱全景轿厢，其示意图如图所示.该摩天轮高128m（即最高点离水面平台MN的距离），圆心O到MN的距离为68m ， 摩天轮匀速旋转一圈用时30 min.某轿厢从点 A 出发，10 min后到达点 B，此过程中，该轿厢所经过的路径（即长度为m.（结果保留π）
6. “轮动发石车”是我国古代的一种投石工具，在春秋战国时期被广泛应用，图1是陈列在展览馆的仿真模型，图2是模型驱动部分的示意图，其中 ， 的半径分别是1cm和10cm，当顺时针转动3周时，上的点P随之旋转 ， 则 ．
7. 已知圆锥底面半径为2cm，母线长为6cm，则该圆锥的侧面积是 cm2 ．8. 如图，四边形ABCD为平行四边形，以点A为圆心，AB长为半径画弧，交BC边于点E ， 连接AE ， AB＝1，∠D＝60°，则的长l＝（结果保留π）．
9. 已知圆锥的底面半径为4，母线长为5，该圆锥的侧面积为 ．10. 如图，AB与⊙O相切于点B ， 连接BO ， 过点O作BO的垂线OC ， 交⊙O于点C ， 连接AC ， 交线段OB于点D ． 若AB＝3，OC＝2，则tanA的值为 ．
11. 如图，正五边形内接于 ， 连接 ， 则的度数为 ．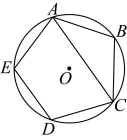
12. 已知圆锥的底面半径为3，高为4，则其侧面积为 ．13. 如图，△ABC是⊙O的内接三角形，∠BAC=45°.若⊙O的半径为2，则劣弧的长为.
14. 将圆锥的侧面沿一条母线剪开后展平，所得扇形的面积为 ， 圆心角θ为 ， 圆锥的底面圆的半径为 ．15. 已知圆锥的底面半径为3，母线长为12，则其侧面展开扇形的圆心角的度数为°．16. 如图，已知正六边形ABCDEF的边长为2，以点E为圆心，EF长为半径作圆，则该圆被正六边形截得的的长为 ．
17. 若用半径为的半圆形纸片围成一个圆锥的侧面，则这个圆锥底面圆的半径为 ．18. 铁艺花窗是园林设计中常见的装饰元素．如图是一个花瓣造型的花窗示意图，由六条等弧连接而成，六条弧所对应的弦构成一个正六边形，中心为点O ， 所在圆的圆心C恰好是△ABO的内心，若 ， 则花窗的周长（图中实线部分的长度） ． （结果保留）
19. 如图，扇形的半径为1，分别以点A、B为圆心，大于的长为半径画弧，两弧相交于点P， ， 则的长（结果保留π）．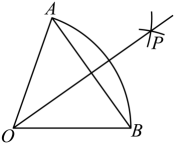
20. 如图，在矩形ABCD中，AB＝4，BC＝4 ， 点E是BC边上的动点，将△ABE沿直线AE翻折得到△APE ， 过点P作PF⊥AD ， 垂足为F ， 点Q是线段AP上一点，且AQPF ． 当点E从点B运动到点C时，点Q运动的路径长是 ．
21. 如图，3个大小完全相同的正六边形无缝隙、不重叠的拼在一起，连接正六边形的三个顶点得到 ， 则的值是 ．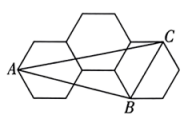
三、证明题
-
22. 如图，PA与⊙O相切于点A，AC为⊙O的直径，点B在⊙O上，连接PB，PC，且PA＝PB．
(1)、连接OB，求证：OB⊥PB；(2)、若∠APB＝60°，PA＝2 ， 求图中阴影部分的面积．23. 如图，AB是⊙O的直径，D是弦AC延长线上的一点，且CD＝CA ， DB的延长线交⊙O于点E ．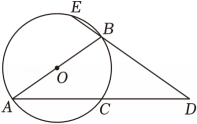
(1)、求证：AB＝BD；(2)、若AB＝3，cos∠ABE＝ ， 求AD的长．四、作图题
-
24. “连弧纹镜”为战国至两汉时期备受推崇的铜镜设计，通常由六到十二个连续的等弧连成一圈，构成了别具一格的装饰图案．图1为徐州博物馆藏“八连弧纹镜”，纹饰中有八个连续的等弧连成一圈．图2为另一件连弧纹镜（残件）的示意图．
(1)、若将图2中的连弧纹镜补全，则该铜镜应为“ 连弧纹镜”；(2)、请用无刻度的直尺与圆规，补全图2中所有残缺的弧，使其“破镜重圆”．（保留作图痕迹，不写作法）25. 如图，在中， ．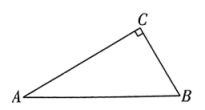
(1)、尺规作图：作 ， 使得圆心在边上，过点且与边相切于点（请保留作图痕迹，标明相应的字母，不写作法）；(2)、在（1）的条件下，若 ， 求与重叠部分的面积．26. 已知AD是的高，是的外接圆.
(1)、请你在图1中用无刻度的直尺和圆规，作的外接圆（保留作图痕迹，不写作法）；(2)、如图2，若的半径为R，求证：；(3)、如图3，延长AD交于点E，过点E的切线交OC的延长线于点F.若 ， ， ， 求CF的长.27. 在中，点在边上，若 ， 则称点是点的“关联点”．
(1)、如图（1），在中，若 ， 于点 ． 试说明：点是点的“关联点”．(2)、如图（2），已知点在线段上，用无刻度的直尺和圆规作一个 ， 使其同时满足下列条件：①点为点的“关联点”；②是钝角（保留作图痕迹，不写作法）．(3)、若为锐角三角形，且点为点的“关联点”．设 ， ， 用含、的代数式表示的取值范围（直接写出结果）．五、解答题
-
28. 如图，⊙O为正三角形ABC的外接圆，直线CD经过点C，CD∥AB．
(1)、判断直线CD与⊙O的位置关系，并说明理由；(2)、若圆的半径为2，求图中阴影部分的面积．29. 如图，点在上，点在外，线段与交于点 ， 过点作的切线交直线于点 ， 且 ．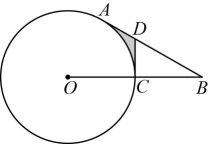
(1)、判断直线与的位置关系，并说明理由；(2)、若 ， ， 求图中阴影部分的面积．30. 如图，△ABC中，AB＝3，AC＝4，BC＝5，⊙A与BC相切于点D ．
(1)、求图中阴影部分的面积；(2)、设⊙A上有一动点P ， 连接CP ， BP ． 当CP的长最大时，求BP的长．31. 如图，点C在以AB为直径的⊙O上，过点C作⊙O的切线l，过点A作AD⊥l，垂足为D，连接AC、BC．
(1)、求证：△ABC∽△ACD；(2)、若AC＝5，CD＝4，求⊙O的半径．32. 如图，等腰三角形的顶角 ， 和底边相切于点 ， 并与两腰 ， 分别相交于 ， 两点，连接 ， ．
(1)、求证：四边形是菱形；(2)、若的半径为2，求图中阴影部分的面积．六、实践探究题
-
33. 材料的疏水性
扬州宝应是荷藕之乡．“微风忽起吹莲叶，青玉盘中泻水银”，莲叶上的水滴来回滚动，不易渗入莲叶内部，这说明莲叶具有较强的疏水性．疏水性是指材料与水相互排斥的一种性质．
【概念理解】
材料疏水性的强弱通常用接触角的大小来描述．材料上的水滴可以近似地看成球或球的一部分，经过球心的纵截面如图1所示，接触角是过固、液、气三相接触点（点M或点N）所作的气﹣液界线的切线与固﹣液界线的夹角，图1中的∠PMN就是水滴的一个接触角．
(1)、请用无刻度的直尺和圆规作出图2中水滴的一个接触角，并用三个大写字母表示接触角；（保留作图痕迹，写出必要的文字说明）(2)、材料的疏水性随着接触角的变大而 （选填“变强”“不变”“变弱”）．(3)、【实践探索】实践中，可以通过测量水滴经过球心的高度BC和底面圆的半径AC（BC⊥AC），求出∠BAC的度数，进而求出接触角∠CAD的度数（如图3）．
请探索图3中接触角∠CAD与∠BAC之间的数量关系（用等式表示），并说明理由．
(4)、【创新思考】材料的疏水性除了用接触角以及图3中与△ABC相关的量描述外，还可以用什么量来描述，请你提出一个合理的设想，并说明疏水性随着此量的变化而如何变化．
34. 综合与实践【问题情境】
如图，小昕同学在正方形纸板ABCD的边AB、BC上分别取点E、F，且AE=BF，AF交DE于点O.连接AC，过点F作FG⊥AC，垂足为G，连接GD、GE，DE交AC于点P，GE交AF于点Q.
(1)、【活动猜想】GD与GE的数量关系是 ， 位置关系是.
(2)、【探索发现】证明（1）中的结论；
(3)、【实践应用】若AD=3，AE=1，求QF的长；
(4)、【综合探究】若AD=3，则当AP=时，△DPG的面积最小.
七、综合题
