备考2026江苏省中考数学一轮复习（真题实练）：命题、四边形及多边形
试卷更新日期：2025-10-28 类型：一轮复习
一、选择题
-
1. 在△ABC中，D、E分别是AB、AC的中点．若DE＝4，则BC的长为（ ）A、2 B、4 C、6 D、82. 如图，在菱形ABCD中，AC、BD是对角线，AB=5.若∠ABD=30°，则AC的长是（ ）
A、4 B、5 C、6 D、103. 如图，在中， ， 点、、分别是边、、的中点，则下列结论错误的是（ ）
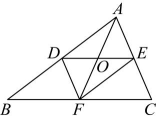A、 B、 C、 D、二、填空题
-
4. 正七边形的内角和为 度．5. 请写出命题“若a＞b ， 则a+1＞b+1”的逆命题： ．6. 若多边形的每个内角都是140°，则这个多边形的边数为 ．7. 若菱形的周长为20cm，且有一个内角为45°，则该菱形的高为 cm．8. 命题“若a＞b ， 则a﹣3＜b﹣3”是命题．（填“真”或“假”）9. 如图，E，F，G，H分别为矩形ABCD各边的中点．若AB＝3，BC＝4，则四边形EFGH的周长为 ．
10. 如图，菱形ABCD的边长为2，∠ABC＝60°，对角线AC、BD相交于点M ． 过点D作AC的平行线交BC的延长线于点N ， 连接MN ． 则MN的长为 ．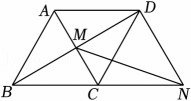
11. 如图，在□ABCD中，E是AD上一点，DE=2AE，CE、BA的延长线相交于点F若AB=2，则AF=.
12. 如图，将矩形纸片沿边折叠，使点在边中点处．若 ， 则 ．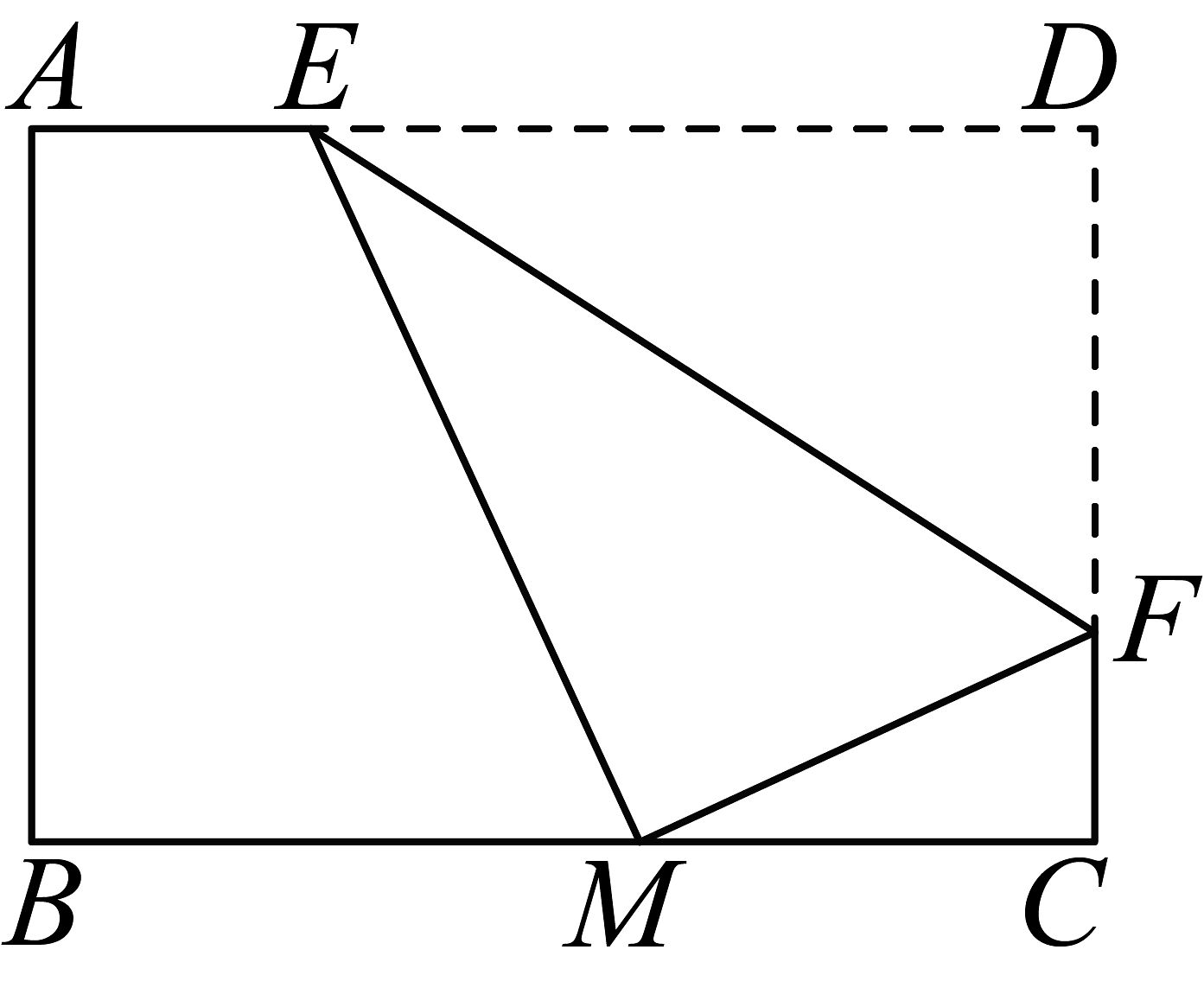
13. 如图，在矩形ABCD中，对角线BD的垂直平分线分别交边AB、CD于点E、F ． 若AD＝8，BE＝10，则tan∠ABD＝ ．
14. 如图，将一张矩形纸片ABCD上下对折，使之完全重合，打开后，得到折痕EF，连接BF．再将矩形纸片折叠，使点落在BF上的点处，折痕为AG．若点恰好为线段BC最靠近点的一个五等分点， ， 则BC的长为 ．
15. 在平行四边形纸片ABCD中，∠ABC＝60°，AB＝4，BC＝8．现将该纸片折叠，折痕与纸片ABCD的两边交于点E、F ． 若E与A重合，F在BC上，且EF⊥BC ， 则被折痕分成的△EBF与四边形EFCD的面积的比为 ；若折痕EF将纸片ABCD分成两个四边形，且被分成的两个四边形的面积的比为1：3，则折痕EF长的取值范围是 ．16. 如图，在菱形ABCD中，AC=4，BD=2，E为线段AC上的动点，四边形DAEF为平行四边形，则BE+BF的最小值为.
三、证明题
-
17. 已知：如图，在▱ABCD中，E为BC的中点，EF⊥AC于点G，交AD于点F，AB⊥AC，连接AE，CF．求证：
(1)、△AGF≌△CGE；(2)、四边形AECF是菱形．18. 请从下列四个命题中选取两个命题，并判断所选命题是真命题还是假命题．如果是真命题，给出证明；如果是假命题，举出反例．⑴若a2＝b2 ， 则a＝b；
⑵对于任意实数x，y，一定有x2+y2＞2xy；
⑶两个连续正奇数的平方差一定是8的倍数；
⑷一组对边平行，另一组对边相等的四边形一定是平行四边形．
19. 如图，在矩形ABCD中，点E在CB延长线上，点F在BC延长线上，且BE＝CF ， 连接AE、DF ．
求证：
(1)、△ABE≌△DCF；(2)、∠EAD＝∠FDA ．20. 已知：如图，四边形为正方形，点E在的延长线上，连接 ．
(1)、求证：；(2)、若 ， 求证： ．四、作图题
-
21. 如图，AC为正方形ABCD的对角线．
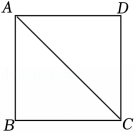(1)、尺规作图：作AD的垂直平分线l交AD于点E ， 在l上确定点F ， 使得点F到∠BAC的两边距离相等；（不写作法，保留痕迹）(2)、在（1）的条件下，求∠EFA的度数．（请直接写出∠EFA的度数）五、解答题
-
22. 如图，C是线段AB 的中点，.
(1)、求证：(2)、 连接DE，若 求 DE 的长.23. 在四边形ABCD中，对角线AC、BD相交于点O，AB=2，AD=1.
(1)、若△ABD是等腰三角形，则BD=(2)、已知OB=OD，AC=BD.①若OA=OC，判断四边形ABCD是怎样的特殊四边形，并说明理由；
②如图，在△ACD中，CD2=AD2+AC2 ， 求AC的长.
24. 如图，在▱ABCD中，对角线AC的垂直平分线与边AD ， BC分别相交于点E ， F ．
(1)、求证：四边形AFCE是菱形；(2)、若AB＝3，BC＝5，CE平分∠ACD ， 求DE的长．六、实践探究题
-
25. 对于平面内的一个四边形，若存在点 ， 使得该四边形的一条对角线绕点旋转一定角度后能与另一条对角线重合，则称该四边形为“可旋四边形”，点是该四边形的一个“旋点”．例如，在矩形中，对角线、相交于点 ， 则点是矩形的一个“旋点”．
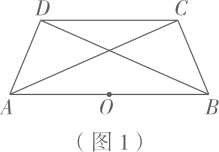
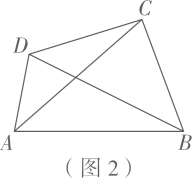(1)、若菱形为“可旋四边形”，其面积是 ， 则菱形的边长是；(2)、如图1，四边形为“可旋四边形”，边的中点是四边形的一个“旋点”．求的度数；(3)、如图2，在四边形中， ， 与不平行．四边形是否为“可旋四边形”？请说明理由．26. 【数学发现】某校数学兴趣小组进行了如下探究：以△ABC内部任意一点O为中心，画出与△ABC成中心对称的△A'B'C' ． 当点O处于不同位置时，从“形”的角度发现两个三角形的重叠部分只可能有两种情况：如图1所示的平行四边形，如图2所示的有三组对边分别平行的六边形（称为“平行六边形”）；从“数”的角度发现两个三角形重叠部分的面积在不断变化．
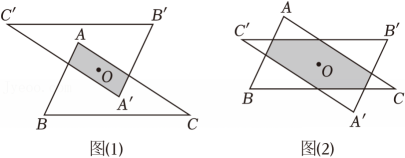
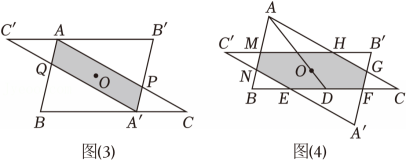
【问题解决】
组员小明选择面积为1的△ABC ， 以其内部任意一点O为中心，画出与之成中心对称的△A'B'C' ， 探究了下列问题，请你帮他解答．
(1)、如图3，BC＝2，当点A关于点O的对称点A'落在边BC上时，两个三角形重叠部分为▱AQA'P ．①若AA'⊥BC ， 求AO的长；（请直接写出答案）
②若▱AQA'P的面积为 ， 求A'C的长．
(2)、如图4，点D为BC的中点，点O在AD上，若两个三角形的重叠部分为“平行六边形”EFGHMN ， 求“平行六边形”EFGHMN面积的最大值，并指出此时点O的位置．27. 问题：如图1，点P为正方形ABCD内一个动点，过点P作EF∥AD ， GH∥AB ， 矩形PHCF的面积是矩形PGAE面积的2倍，探索∠FAH的度数随点P运动的变化情况．
【从特例开始】
(1)、小玲利用正方形网格画出了一个符合条件的特殊图形（如图2），请你仅用无刻度的直尺连接一条线段，由此可得此图形中∠FAH＝ °．(2)、小亮也画出了一个符合条件的特殊图形（如图3），其中PE＝PF＝6，PG＝4，PH＝8，求此图形中∠FAH的度数；(3)、【一般化探索】利用图1，探索上述问题中∠FAH的度数随点P运动的变化情况，并说明理由．
七、综合题
-
28. 如图1，将Rt△AOB绕直角顶点O旋转至△COD，点A，B的对应点分别为C，D．连接AD，BC，AC，BD，直线AC与BD交于点E．
(1)、△AOD与△BOC的面积存在怎样的数量关系？请说明理由；(2)、如图2，连接OE，若AB，CD，OE的中点分别为P，Q，R．求证：P，Q，R三点共线；(3)、已知AB＝5，随着OA，OB及旋转角的变化，若存在以A，B，C，D为顶点的四边形，其面积为S，则S的最大值为 ．29. 如图，矩形ABCD中，对角线AC，BD相交于点O．M是BC的中点，DM交AC于点G．
(1)、求证：AG＝2GC；(2)、设∠BCD，∠BDC的角平分线交于点I．①当AB＝6，BC＝8时，求点I到BC的距离；
②若AB+AC＝2BC，作直线GI分别交BD，CD于E，F两点，求的值．
30. 如图1，在矩形中， ， 点是边上一个动点，点在射线上， ． 线段的垂直平分线分别交直线于点、、、 ．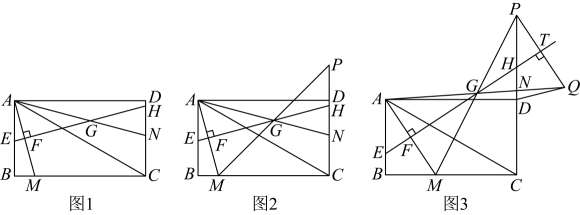
(1)、直接写出°，；(2)、当时，求的值；(3)、如图2，连接并延长交直线于点 ．①求证：；
②如图3，过点作直线的垂线，分别交直线于点 ， 连接 ， 求线段的最小值．
-