备考2026江苏省中考数学一轮复习(真题实练):相交、平行及三角形
试卷更新日期:2025-10-28 类型:一轮复习
一、选择题
-
1. 如图,将两块相同的直角三角尺按图示摆放,则AB与CD平行这一判断过程体现的数学依据是( )
 A、垂线段最短 B、内错角相等,两直线平行 C、两点确定一条直线 D、平行于同一条直线的两条直线平行2. 如图,在A,B两地间修一条笔直的公路,从A地测得公路的走向为北偏东 若A,B两地同时开工,要使公路准确接通,则 的度数应为( )
A、垂线段最短 B、内错角相等,两直线平行 C、两点确定一条直线 D、平行于同一条直线的两条直线平行2. 如图,在A,B两地间修一条笔直的公路,从A地测得公路的走向为北偏东 若A,B两地同时开工,要使公路准确接通,则 的度数应为( ) A、 B、 C、 D、3. 如图,将直角三角形绕它的一条直角边所在直线旋转一周后形成的几何体是( )
A、 B、 C、 D、3. 如图,将直角三角形绕它的一条直角边所在直线旋转一周后形成的几何体是( )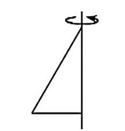 A、
A、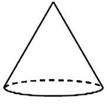 B、
B、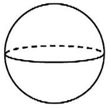 C、
C、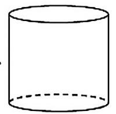 D、
D、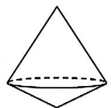 4. 如图,在△ABC中,BC=7,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,则△AEG的周长为( )
4. 如图,在△ABC中,BC=7,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,则△AEG的周长为( ) A、5 B、6 C、7 D、85. 下列长度(单位:cm)的3根小木棒能搭成三角形的是( )A、1,2,3 B、2,3,4 C、3,5,8 D、4,5,106. 如图,在中, , , , 则( )
A、5 B、6 C、7 D、85. 下列长度(单位:cm)的3根小木棒能搭成三角形的是( )A、1,2,3 B、2,3,4 C、3,5,8 D、4,5,106. 如图,在中, , , , 则( ) A、 B、 C、 D、7. 如图,直线a∥b , 矩形ABCD的顶点A在直线b上,若∠2=41°,则∠1的度数为( )
A、 B、 C、 D、7. 如图,直线a∥b , 矩形ABCD的顶点A在直线b上,若∠2=41°,则∠1的度数为( ) A、41° B、51° C、49° D、59°8. 上午9时整,钟表的时针和分针构成的角的度数为( )A、30° B、60° C、90° D、120°9. 七巧板具有深厚的中华文化底蕴,它是由正方形、平行四边形和大小不一的等腰直角三角形组成的.小明用七巧板拼成的丹顶鹤如图所示,且过点C作直线AB∥DE.若∠1=20°,则∠2的度数是( )
A、41° B、51° C、49° D、59°8. 上午9时整,钟表的时针和分针构成的角的度数为( )A、30° B、60° C、90° D、120°9. 七巧板具有深厚的中华文化底蕴,它是由正方形、平行四边形和大小不一的等腰直角三角形组成的.小明用七巧板拼成的丹顶鹤如图所示,且过点C作直线AB∥DE.若∠1=20°,则∠2的度数是( )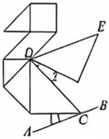 A、15° B、20° C、25° D、30°10. 如图,平行于主光轴PQ的光线AB和CD经过凸透镜折射后,折射光线BE , DF交于主光轴上一点G . 若∠ABE=130°,∠CDF=150°,则∠EGF的度数是( )
A、15° B、20° C、25° D、30°10. 如图,平行于主光轴PQ的光线AB和CD经过凸透镜折射后,折射光线BE , DF交于主光轴上一点G . 若∠ABE=130°,∠CDF=150°,则∠EGF的度数是( ) A、60° B、70° C、80° D、90°11. 在如图的房屋人字梁架中,AB=AC , 点D在BC上,下列条件不能说明AD⊥BC的是( )
A、60° B、70° C、80° D、90°11. 在如图的房屋人字梁架中,AB=AC , 点D在BC上,下列条件不能说明AD⊥BC的是( ) A、∠ADB=∠ADC B、∠B=∠C C、BD=CD D、AD平分∠BAC12. 如图, , 若 , , 则的度数为( )
A、∠ADB=∠ADC B、∠B=∠C C、BD=CD D、AD平分∠BAC12. 如图, , 若 , , 则的度数为( ) A、45° B、55° C、60° D、65°13. 如图,在纸上画有∠AOB , 将两把直尺按图示摆放,直尺边缘的交点P在∠AOB的平分线上,则( )
A、45° B、55° C、60° D、65°13. 如图,在纸上画有∠AOB , 将两把直尺按图示摆放,直尺边缘的交点P在∠AOB的平分线上,则( ) A、d1与d2一定相等 B、d1与d2一定不相等 C、l1与l2一定相等 D、l1与l2一定不相等14. “赵爽弦图”巧妙利用面积关系证明了勾股定理.如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼成的一个大正方形.设直角三角形的两条直角边长分别为m , n(m>n).若小正方形面积为5,(m+n)2=21,则大正方形面积为( )
A、d1与d2一定相等 B、d1与d2一定不相等 C、l1与l2一定相等 D、l1与l2一定不相等14. “赵爽弦图”巧妙利用面积关系证明了勾股定理.如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼成的一个大正方形.设直角三角形的两条直角边长分别为m , n(m>n).若小正方形面积为5,(m+n)2=21,则大正方形面积为( ) A、12 B、13 C、14 D、15
A、12 B、13 C、14 D、15二、填空题
-
15. 如图, 以O为圆心,2为半径画弧,分别交OM,ON 于 A,B 两点,再分别以A,B为圆心, 为半径画弧,两弧在. 内部相交于点C,作射线OC,连接AC,BC,则 . (结果保留根号)
 16. 如图,长为3m的梯子靠在墙上,梯子的底端离墙脚线的距离为1.8m,则梯子顶端的高度h为m.
16. 如图,长为3m的梯子靠在墙上,梯子的底端离墙脚线的距离为1.8m,则梯子顶端的高度h为m. 17. 如图,AB//CD,直线AB与射线DE相交于点O.若∠D=50°,则∠BOE=°
17. 如图,AB//CD,直线AB与射线DE相交于点O.若∠D=50°,则∠BOE=° 18. 如图,△ABC的边AB的垂直平分线交AC于点D , 连接BD . 若AC=8,CD=5,则BD= .
18. 如图,△ABC的边AB的垂直平分线交AC于点D , 连接BD . 若AC=8,CD=5,则BD= . 19. 等腰三角形的两边长分别为6和2,则第三边长为 .20. 如图,将三角形纸片ABC折叠,使点A落在边BC上的点D处,折痕为CE.若△ABC的面积为8,△BCE的面积为5,则BD:DC= .
19. 等腰三角形的两边长分别为6和2,则第三边长为 .20. 如图,将三角形纸片ABC折叠,使点A落在边BC上的点D处,折痕为CE.若△ABC的面积为8,△BCE的面积为5,则BD:DC= . 21. 南通是“建筑之乡”,工程建筑中经常采用三角形的结构.如图是屋架设计图的一部分,E是斜梁AC的中点,立柱AD,EF垂直于横梁BC.若AC=4.8m,∠C=30°,则EF的长为 m.
21. 南通是“建筑之乡”,工程建筑中经常采用三角形的结构.如图是屋架设计图的一部分,E是斜梁AC的中点,立柱AD,EF垂直于横梁BC.若AC=4.8m,∠C=30°,则EF的长为 m. 22. 如图AB∥CD,AC⊥AD,∠ACD=50°,则∠α=.
22. 如图AB∥CD,AC⊥AD,∠ACD=50°,则∠α=. 23. 等腰三角形的两边长分别为和 , 则该等腰三角形的周长为 .24. 如图,在△ABC中,点D , E分别是边AB , BC的中点,点F在线段DE的延长线上,且∠BFC=90°.若AC=4,BC=8,则DF的长是 .
23. 等腰三角形的两边长分别为和 , 则该等腰三角形的周长为 .24. 如图,在△ABC中,点D , E分别是边AB , BC的中点,点F在线段DE的延长线上,且∠BFC=90°.若AC=4,BC=8,则DF的长是 . 25. 如图,在△ABC中,∠B=50°,∠C=30°,AD是高,以点A为圆心,AB长为半径画弧,交AC于点E , 再分别以B、E为圆心,大于BE的长为半径画弧,两弧在∠BAC的内部交于点F , 作射线AF , 则∠DAF=°.
25. 如图,在△ABC中,∠B=50°,∠C=30°,AD是高,以点A为圆心,AB长为半径画弧,交AC于点E , 再分别以B、E为圆心,大于BE的长为半径画弧,两弧在∠BAC的内部交于点F , 作射线AF , 则∠DAF=°. 26. 如图,直线 , 直线 , 则°.
26. 如图,直线 , 直线 , 则°. 27. 勾股数是指能成为直角三角形三条边长的三个正整数,世界上第一次给出勾股数公式的是中国古代数学著作《九章算术》.现有勾股数a , b , c , 其中 , 均小于 , , , 是大于1的奇数,则(用含的式子表示).28. 如图,在中, , 点在边上(不与A,B重合),过点作 , 垂足为点 , 则的最小值是 .
27. 勾股数是指能成为直角三角形三条边长的三个正整数,世界上第一次给出勾股数公式的是中国古代数学著作《九章算术》.现有勾股数a , b , c , 其中 , 均小于 , , , 是大于1的奇数,则(用含的式子表示).28. 如图,在中, , 点在边上(不与A,B重合),过点作 , 垂足为点 , 则的最小值是 .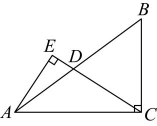 29. 如图,在 中, , D是线段BC上一点(不与端点B,C重合),连接AD,以AD为边,在AD 的右侧作等边三角形ADE,线段 DE 与线段AC交于点F,则线段CF 长度的最大值为.
29. 如图,在 中, , D是线段BC上一点(不与端点B,C重合),连接AD,以AD为边,在AD 的右侧作等边三角形ADE,线段 DE 与线段AC交于点F,则线段CF 长度的最大值为.
三、证明题
-
30. 如图,点D在△ABC的边AB上,DF经过边AC的中点E , 且EF=DE . 求证:CF∥AB .
 31. 如图,△ABC中, , 分别以B , C为圆心,大于长为半径画弧,两弧交于点D , 连接BD , CD , AD , AD与BC交于点E .
31. 如图,△ABC中, , 分别以B , C为圆心,大于长为半径画弧,两弧交于点D , 连接BD , CD , AD , AD与BC交于点E . (1)、求证:;(2)、若 , , 求BC的长.
(1)、求证:;(2)、若 , , 求BC的长.四、作图题
-
32. 如图,在△ABC中,AB=AC,点D,E在BC上,BD=CE
 (1)、求证:△ABD≌△ACE(2)、用直尺和圆规作∠DAE的平分线AF(保留作图痕迹,不要求写作法)33. 如图,AB与CD相交于点 .
(1)、求证:△ABD≌△ACE(2)、用直尺和圆规作∠DAE的平分线AF(保留作图痕迹,不要求写作法)33. 如图,AB与CD相交于点 . (1)、求证:;(2)、用无刻度的直尺和圆规作图:求作菱形DMCN,使得点在AC上,点在BD上.(不写作法,保留作图痕迹,标明字母)
(1)、求证:;(2)、用无刻度的直尺和圆规作图:求作菱形DMCN,使得点在AC上,点在BD上.(不写作法,保留作图痕迹,标明字母)五、解答题
-
34. 如图,∠C=∠D=90°,∠CBA=∠DAB .
 (1)、求证:△ABC≌△BAD;(2)、若∠DAB=70°,则∠CAB=°.35. 如图,B、E、C、F是直线l上的四点,AC、DE相交于点G , AB=DF , AC=DE , BC=EF .
(1)、求证:△ABC≌△BAD;(2)、若∠DAB=70°,则∠CAB=°.35. 如图,B、E、C、F是直线l上的四点,AC、DE相交于点G , AB=DF , AC=DE , BC=EF . (1)、求证:△GEC是等腰三角形;(2)、连接AD , 则AD与l的位置关系是 .
(1)、求证:△GEC是等腰三角形;(2)、连接AD , 则AD与l的位置关系是 .六、实践探究题
-
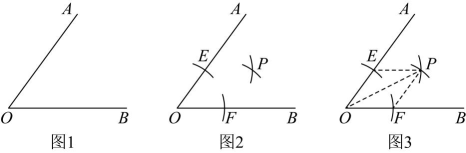
36. 实验活动:仅用一把圆规作图.(1)、【任务阅读】如图 , 仅用一把圆规在内部画一点 , 使点在的平分线上.
小明的作法如下:
如图 , 以点为圆心,适当长为半径画弧,分别交射线于点 , 再分别以点、为圆心,大于长为半径画弧,两弧交于点 , 则点为所求点.理由:如图3,连接 , 由作图可知 , ,
又因为 ,
所以 .
所以 ,
所以平分 ,
即点为所求点;
 (2)、【实践操作】如图 , 已知直线及其外一点 , 只用一把圆规画一点 , 使点所在直线与直线平行,并给出证明.(保留作图痕迹,不写作法)
(2)、【实践操作】如图 , 已知直线及其外一点 , 只用一把圆规画一点 , 使点所在直线与直线平行,并给出证明.(保留作图痕迹,不写作法)