备考2026江苏省中考数学一轮复习(真题实练):二次函数
试卷更新日期:2025-10-27 类型:一轮复习
一、选择题
-
1. 将抛物线y=x2+2x﹣1向右平移3个单位后得到新抛物线的顶点坐标为( )A、(﹣4,﹣1) B、(﹣4,2) C、(2,1) D、(2,﹣2)2. 在平面直角坐标系xOy中,五个点的坐标分别为A(﹣1,5),B(1,2),C(2,1),D(3,﹣1),E(5,5).若抛物线y=a(x﹣2)2+k(a>0)经过上述五个点中的三个点,则满足题意的a的值不可能为( )A、 B、 C、 D、3. 若实数 , , 满足 , , 则代数式的值可以是( )A、 B、 C、 D、4. 已知二次函数图象的一部分如图所示,该函数图象经过点 , 对称轴为直线 . 对于下列结论:①;②;③多项式可因式分解为;④当时,关于的方程无实数根.其中正确的个数有( )
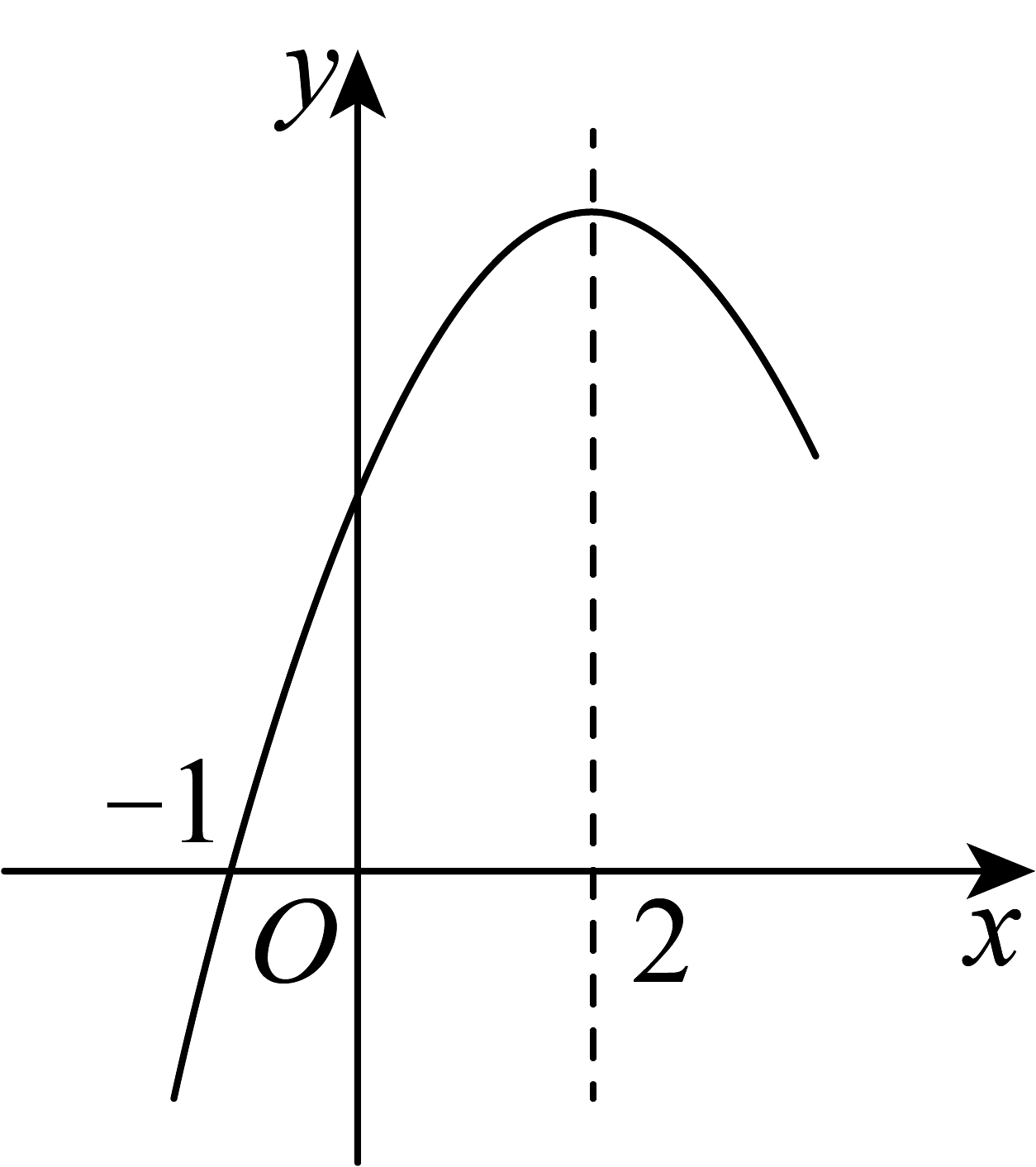 A、1个 B、2个 C、3个 D、4个5. 如图,在四边形中, , , , 若线段在边上运动,且 , 则的最小值是( )
A、1个 B、2个 C、3个 D、4个5. 如图,在四边形中, , , , 若线段在边上运动,且 , 则的最小值是( ) A、 B、 C、 D、10
A、 B、 C、 D、10二、填空题
-
6. 如图为二次函数y=ax2+bx+c的图象,下列代数式的值为负数的是 (写出所有正确结果的序号).
①a;
②2a+b;
③c;
④b2﹣4ac;
⑤a﹣b+c.
 7. 二次函数y=x2+x+1的最小值为 .8. 已知二次函数y=x2﹣2x﹣3,当自变量x满足0≤x≤4时,y的取值范围是 .9. 一块梯形木板 , 按如图方式设计一个矩形桌面(点在边上).当时,矩形桌面面积最大.
7. 二次函数y=x2+x+1的最小值为 .8. 已知二次函数y=x2﹣2x﹣3,当自变量x满足0≤x≤4时,y的取值范围是 .9. 一块梯形木板 , 按如图方式设计一个矩形桌面(点在边上).当时,矩形桌面面积最大. 10. 如图,小亮同学掷铅球时,铅球沿抛物线y=a(×-3)2+2.5运行,其中x是铅球离初始位置的水平距离,y是铅球离地面的高度.若铅球抛出时离地面的高度OA为1.6m,则铅球掷出的水平距离OB为m.
10. 如图,小亮同学掷铅球时,铅球沿抛物线y=a(×-3)2+2.5运行,其中x是铅球离初始位置的水平距离,y是铅球离地面的高度.若铅球抛出时离地面的高度OA为1.6m,则铅球掷出的水平距离OB为m. 11. 二次函数的最大值为 .12. 二次函数的图像与x轴交于点、 , 与轴交于点 , 过点的直线将分成两部分,这两部分是三角形或梯形,且面积相等,则的值为 .
11. 二次函数的最大值为 .12. 二次函数的图像与x轴交于点、 , 与轴交于点 , 过点的直线将分成两部分,这两部分是三角形或梯形,且面积相等,则的值为 .三、解答题
-
13. 急刹车时,停车距离是指骑车人从意识到应当刹车到车辆停下来所走的距离,记作ym;反应距离是指骑车人意识到应当刹车到实施刹车所走的距离,记作d1m;刹车距离是指骑车人实施刹车到车辆停下来所走的距离,记作d2m,已知y=d1+d2 , d1与骑行速度成正比,d2与骑行速度的平方成正比.当骑行速度为13km/h时,反应距离为2.6m,刹车距离为1m.(1)、若骑行速度为26km/h,则d1= m,d2= m;(2)、设骑行速度为xkm/h,求y关于x的函数表达式;(3)、当刹车距离为2m时,停车距离为多少?(精确到0.1m,参考数据: , , )14. 如图:在平面直角坐标系xOy中,一次函数的图像分别与x轴y抽交于点A、B,点C是线段AB上一点C与B不重合).二次函数(a,b,c是常数,且)的图像经过点B,顶点是C.将该二次函数的图象平移后得到新抛物线,B'、C分别是B、C的对应点,且点B'落在x轴正半轴上,点C'的纵坐标为-2.
 (1)、OB=;(2)、求点C的坐标;(3)、已知新抛物线与y抽交于点G(0,)点D(3,y1)、E(x2 , y2)在新抛物线上,若对于满足的任意实数 , 总成立,求实数m的取值范围.15. 已知二次函数y=x2+2(a+1)x+3a2-2a+3,a为常数.(1)、若该二次函数的图象与直线y=2a2有两个交点,求a的取值范围;(2)、若该二次函数的图象与x轴有交点,求a的值;(3)、求证:该二次函数的图象不经过原点.16. 在校园科技节期间,科普员为同学们进行了水火箭的发射表演,图1是某型号水火箭的实物图,水火箭发射后的运动路线可以看作是一条抛物线.为了解水火箭的相关性能,同学们进一步展开研究.如图2建立直角坐标系,水火箭发射后落在水平地面A处.科普员提供了该型号水火箭与地面成一定角度时,从发射到着陆过程中,水火箭距离地面的竖直高度与离发射点O的水平距离的几组关系数据如下:
(1)、OB=;(2)、求点C的坐标;(3)、已知新抛物线与y抽交于点G(0,)点D(3,y1)、E(x2 , y2)在新抛物线上,若对于满足的任意实数 , 总成立,求实数m的取值范围.15. 已知二次函数y=x2+2(a+1)x+3a2-2a+3,a为常数.(1)、若该二次函数的图象与直线y=2a2有两个交点,求a的取值范围;(2)、若该二次函数的图象与x轴有交点,求a的值;(3)、求证:该二次函数的图象不经过原点.16. 在校园科技节期间,科普员为同学们进行了水火箭的发射表演,图1是某型号水火箭的实物图,水火箭发射后的运动路线可以看作是一条抛物线.为了解水火箭的相关性能,同学们进一步展开研究.如图2建立直角坐标系,水火箭发射后落在水平地面A处.科普员提供了该型号水火箭与地面成一定角度时,从发射到着陆过程中,水火箭距离地面的竖直高度与离发射点O的水平距离的几组关系数据如下:水平距离
0
3
4
10
15
20
22
27
竖直高度
0
3.24
4.16
8
9
8
7.04
3.24
 (1)、根据上表,请确定抛物线的表达式;(2)、请计算当水火箭飞行至离发射点O的水平距离为时,水火箭距离地面的竖直高度.17. 本小题分
(1)、根据上表,请确定抛物线的表达式;(2)、请计算当水火箭飞行至离发射点O的水平距离为时,水火箭距离地面的竖直高度.17. 本小题分如图,已知二次函数的图像与轴交于 , 两点.
 (1)、求的值.(2)、若点在该二次函数的图象上,且的面积为 , 求点的坐标.18. 已知二次函数(为常数).(1)、该函数图象与轴交于两点,若点坐标为 ,
(1)、求的值.(2)、若点在该二次函数的图象上,且的面积为 , 求点的坐标.18. 已知二次函数(为常数).(1)、该函数图象与轴交于两点,若点坐标为 ,①则的值是 ▲ , 点的坐标是 ▲ ;
②当时,借助图像,求自变量的取值范围;
(2)、对于一切实数 , 若函数值总成立,求的取值范围(用含的式子表示);(3)、当时(其中为实数,),自变量的取值范围是 , 求和的值以及的取值范围.19. 定义:在平面直角坐标系中,到两个坐标轴的距离都小于或等于的点叫“阶近轴点”,所有的“阶近轴点”组成的图形记为图形 . 如图所示,所有的“1阶近轴点”组成的图形是以坐标原点为中心,2为边长的正方形区域.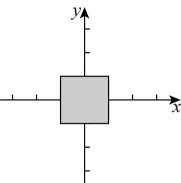 (1)、下列函数图象上存在“1阶近轴点”的是;
(1)、下列函数图象上存在“1阶近轴点”的是;①;②;③ .
(2)、若一次函数的图像上存在“3阶近轴点”,求实数的取值范围;(3)、特别地,当点在图形上,且横坐标是纵坐标的倍时,称点是图形的“阶完美点”,若二次函数的图像上有且只有一个“2阶完美点”,求实数的取值范围.20. 如图,二次函数的图象与x轴相交于点 , 其顶点是C .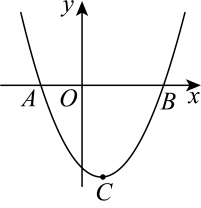
 (1)、;(2)、D是第三象限抛物线上的一点,连接OD , ;将原抛物线向左平移,使得平移后的抛物线经过点D , 过点作x轴的垂线l . 已知在l的左侧,平移前后的两条抛物线都下降,求k的取值范围;(3)、将原抛物线平移,平移后的抛物线与原抛物线的对称轴相交于点Q , 且其顶点P落在原抛物线上,连接PC、QC、PQ . 已知是直角三角形,求点P的坐标.
(1)、;(2)、D是第三象限抛物线上的一点,连接OD , ;将原抛物线向左平移,使得平移后的抛物线经过点D , 过点作x轴的垂线l . 已知在l的左侧,平移前后的两条抛物线都下降,求k的取值范围;(3)、将原抛物线平移,平移后的抛物线与原抛物线的对称轴相交于点Q , 且其顶点P落在原抛物线上,连接PC、QC、PQ . 已知是直角三角形,求点P的坐标.四、实践探究题
-
21. 【生活观察】小明通过观察发现,将运动中的羽毛球看成一个点,扣杀球和网前吊球这两种击球的运动路线可以近似抽象成如下两种路线,如图1和图2所示.

【数学建模】小明发现扣杀球的路线近似为一条直线,网前吊球的路线近似为抛物线.羽毛球运动轨迹的剖面如图3所示,从A点击球,击球点是抛物线的最高点,点A到地面的距离AO=2.4m,球网上端点B到地面的距离BC=1.55m,人与球网之间的距离OC=1.6m,假设两种击球路线都经过点B正上方0.05m处的点D,网前吊球和扣杀球的落点分别为点E,F.
(1)、请在图3中建立合适的平面直角坐标系,并分别求出两种击球路线的函数表达式.(2)、【模型应用】网前吊球的落点到球网的距离CE的长是 m;
(3)、甲在A处击球,扣杀球时,羽毛球的平均速度约为36m/s,网前吊球时,羽毛球下降的高度h(单位:m)与时间t(单位:s)之间的关系式为h=5t2.乙在看到甲击球的同时尝试接球,从甲击球到乙能成功接球的时间至少需要0.5s.请通过计算说明,乙能接到哪种方式的击球.22. 综合与实践:学校数学兴趣小组围绕“校园花圃方案设计”开展主题学习活动.已知花圃一边靠墙(墙的长度不限),其余部分用总长为60m的栅栏围成.兴趣小组设计了以下两种方案:
方案一
方案二
如图1,围成一个面积为450m2的矩形花圃.

如图2,围成矩形花圃时,用栅栏(栅栏宽度忽略不计)将该花圃分隔为两个小矩形区域,用来种植不同花卉,并在花圃两侧各留一个宽为3m的进出口(此处不用栅栏).
 (1)、求方案一中与墙垂直的边的长度;(2)、要使方案二中花圃的面积最大,与墙平行的边的长度为多少米?23. 定义:平面直角坐标系中,点 , 点 , 若 , , 其中为常数,且 , 则称点是点的“级变换点”.例如,点是点的“级变换点”.(1)、函数的图象上是否存在点的“级变换点”?若存在,求出的值;若不存在,说明理由;(2)、点与其“级变换点” 分别在直线 , 上,在 , 上分别取点 , . 若 , 求证:;(3)、关于x的二次函数的图象上恰有两个点,这两个点的“1级变换点”都在直线上,求n的取值范围.24. 规定:若函数的图像与函数的图像有三个不同的公共点,则称这两个函数互为“兄弟函数”,其公共点称为“兄弟点”.(1)、下列三个函数①;②;③ , 其中与二次函数互为“兄弟函数”的是(填写序号);(2)、若函数与互为“兄弟函数”,是其中一个“兄弟点”的横坐标.
(1)、求方案一中与墙垂直的边的长度;(2)、要使方案二中花圃的面积最大,与墙平行的边的长度为多少米?23. 定义:平面直角坐标系中,点 , 点 , 若 , , 其中为常数,且 , 则称点是点的“级变换点”.例如,点是点的“级变换点”.(1)、函数的图象上是否存在点的“级变换点”?若存在,求出的值;若不存在,说明理由;(2)、点与其“级变换点” 分别在直线 , 上,在 , 上分别取点 , . 若 , 求证:;(3)、关于x的二次函数的图象上恰有两个点,这两个点的“1级变换点”都在直线上,求n的取值范围.24. 规定:若函数的图像与函数的图像有三个不同的公共点,则称这两个函数互为“兄弟函数”,其公共点称为“兄弟点”.(1)、下列三个函数①;②;③ , 其中与二次函数互为“兄弟函数”的是(填写序号);(2)、若函数与互为“兄弟函数”,是其中一个“兄弟点”的横坐标.①求实数a的值;
②直接写出另外两个“兄弟点”的横坐标是 ▲ 、 ▲ ;
(3)、若函数(m为常数)与互为“兄弟函数”,三个“兄弟点”的横坐标分别为、、 , 且 , 求的取值范围.五、综合题
-
25. 已知二次函数y=﹣m(m≠0)图象的顶点为A , 与y轴交于点B , 对称轴与x轴交于点C .(1)、若该函数图象经过点 , 求点A的横坐标;(2)、若m<3,点P(2,y1)和Q(4,y2)在该函数图象上,证明:y1>y2;(3)、若△ABC是等腰三角形,求m的值.26. 一块直角三角形木板,它的一条直角边BC长2m,面积为1.5m2.(1)、甲、乙两人分别按图1、图2用它设计一个正方形桌面,请说明哪个正方形面积较大;
 (2)、丙、丁两人分别按图3、图4用它设计一个长方形桌面.请分别求出图3、图4中长方形的面积y(m2)与DE的长x(m)之间的函数表达式,并分别求出面积的最大值
(2)、丙、丁两人分别按图3、图4用它设计一个长方形桌面.请分别求出图3、图4中长方形的面积y(m2)与DE的长x(m)之间的函数表达式,并分别求出面积的最大值 27. 如图,在平面直角坐标系中,二次函数y=﹣x2﹣2x+3的图象(记为G1)与x轴交于点A , B , 与y轴交于点C , 二次函数y=x2+bx+c的图象(记为G2)经过点A , C . 直线x=t与两个图象G1 , G2分别交于点M , N , 与x轴交于点P .
27. 如图,在平面直角坐标系中,二次函数y=﹣x2﹣2x+3的图象(记为G1)与x轴交于点A , B , 与y轴交于点C , 二次函数y=x2+bx+c的图象(记为G2)经过点A , C . 直线x=t与两个图象G1 , G2分别交于点M , N , 与x轴交于点P . (1)、求b , c的值.(2)、当点P在线段AO上时,求MN的最大值.(3)、设点M , N到直线AC的距离分别为m , n . 当m+n=4时,对应的t值有 个;当m﹣n=3时,对应的t值有 个;当mn=2时,对应的t值有 个;当1时,对应的t值有 个.28. 如图,△ABC中, , , , , 反比例函数的图象与AB交于点 , 与BC交于点E .
(1)、求b , c的值.(2)、当点P在线段AO上时,求MN的最大值.(3)、设点M , N到直线AC的距离分别为m , n . 当m+n=4时,对应的t值有 个;当m﹣n=3时,对应的t值有 个;当mn=2时,对应的t值有 个;当1时,对应的t值有 个.28. 如图,△ABC中, , , , , 反比例函数的图象与AB交于点 , 与BC交于点E . (1)、求m , k的值;(2)、点P为反比例函数图象上一动点(点P在D , E之间运动,不与D , E重合),过点P作 , 交y轴于点M , 过点P作轴,交BC于点N , 连接MN , 求△PMN面积的最大值,并求出此时点P的坐标.29. 某商场销售两种商品,每件进价均为20元.调查发现,如果售出种20件,种10件,销售总额为840元;如果售出种10件,种15件,销售总额为660元.(1)、求两种商品的销售单价.(2)、经市场调研,种商品按原售价销售,可售出40件,原售价每降价1元,销售量可增加10件;种商品的售价不变,种商品售价不低于种商品售价.设种商品降价元,如果两种商品销售量相同,求取何值时,商场销售两种商品可获得总利润最大?最大利润是多少?30. 阅读下面方框内的内容,并完成相应的任务.
(1)、求m , k的值;(2)、点P为反比例函数图象上一动点(点P在D , E之间运动,不与D , E重合),过点P作 , 交y轴于点M , 过点P作轴,交BC于点N , 连接MN , 求△PMN面积的最大值,并求出此时点P的坐标.29. 某商场销售两种商品,每件进价均为20元.调查发现,如果售出种20件,种10件,销售总额为840元;如果售出种10件,种15件,销售总额为660元.(1)、求两种商品的销售单价.(2)、经市场调研,种商品按原售价销售,可售出40件,原售价每降价1元,销售量可增加10件;种商品的售价不变,种商品售价不低于种商品售价.设种商品降价元,如果两种商品销售量相同,求取何值时,商场销售两种商品可获得总利润最大?最大利润是多少?30. 阅读下面方框内的内容,并完成相应的任务.小丽学习了方程、不等式、函数后提出如下问题:如何求不等式的解集?
通过思考,小丽得到以下3种方法:
方法1:方程的两根为 , , 可得函数的图象与x轴的两个交点横坐标为、 , 画出函数图象,观察该图象在x轴下方的点,其横坐标的范围是不等式的解集.
方法2:不等式可变形为 , 问题转化为研究函数与的图象关系.画出函数图象,观察发现:两图象的交点横坐标也是、3;的图象在的图象下方的点,其横坐标的范围是该不等式的解集.
方法3:当时,不等式一定成立;当时,不等式变为;当时,不等式变为 . 问题转化为研究函数与的图象关系…
任务:
(1)、不等式的解集为;(2)、3种方法都运用了____数学思想方法(从下面选项中选1个序号即可);A、分类讨论 B、转化思想 C、特殊到一般 D、数形结合31. 如图,二次函数 的图像与x轴交于A,B两点(点A 在点B 的左侧),与y轴交于点C,作直线 BC, 为二次函数 图像上两点. (1)、求直线 BC 对应函数的表达式;(2)、试判断是否存在实数m使得 若存在,求出m的值;若不存在,请说明理由.(3)、已知 P 是二次函数 图像上一点(不与点 M,N重合),且点 P 的横坐标为 作 若直线 BC 与线段 MN,MP 分别交于点 D,E,且 与 的面积的比为1:4,请直接写出所有满足条件的m 的值.32. 如图,二次函数的图像与轴分别交于点(点A在点的左侧),直线是对称轴.点在函数图象上,其横坐标大于4,连接 , 过点作 , 垂足为 , 以点为圆心,作半径为的圆,与相切,切点为 .
(1)、求直线 BC 对应函数的表达式;(2)、试判断是否存在实数m使得 若存在,求出m的值;若不存在,请说明理由.(3)、已知 P 是二次函数 图像上一点(不与点 M,N重合),且点 P 的横坐标为 作 若直线 BC 与线段 MN,MP 分别交于点 D,E,且 与 的面积的比为1:4,请直接写出所有满足条件的m 的值.32. 如图,二次函数的图像与轴分别交于点(点A在点的左侧),直线是对称轴.点在函数图象上,其横坐标大于4,连接 , 过点作 , 垂足为 , 以点为圆心,作半径为的圆,与相切,切点为 .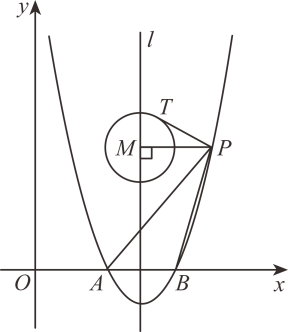 (1)、求点的坐标;(2)、若以的切线长为边长的正方形的面积与的面积相等,且不经过点 , 求长的取值范围.33. 在平面直角坐标系中,已知点A在y轴正半轴上.
(1)、求点的坐标;(2)、若以的切线长为边长的正方形的面积与的面积相等,且不经过点 , 求长的取值范围.33. 在平面直角坐标系中,已知点A在y轴正半轴上. (1)、如果四个点中恰有三个点在二次函数(a为常数,且)的图象上.
(1)、如果四个点中恰有三个点在二次函数(a为常数,且)的图象上.① ▲ ;
②如图1,已知菱形的顶点B、C、D在该二次函数的图象上,且轴,求菱形的边长;
③如图2,已知正方形的顶点B、D在该二次函数的图象上,点B、D在y轴的同侧,且点B在点D的左侧,设点B、D的横坐标分别为m、n,试探究是否为定值.如果是,求出这个值;如果不是,请说明理由.
(2)、已知正方形的顶点B、D在二次函数(a为常数,且)的图象上,点B在点D的左侧,设点B、D的横坐标分别为m、n,直接写出m、n满足的等量关系式.34. 已知二次函数的自变量的部分取值和对应函数值如下表:…
0
1
2
3
…
…
4
3
0
…
(1)、求二次函数的表达式;(2)、将二次函数的图象向右平移个单位,得到二次函数的图象,使得当时,随增大而增大;当时,随增大而减小,请写出一个符合条件的二次函数的表达式 , 实数的取值范围是;(3)、、、是二次函数的图象上互不重合的三点.已知点、的横坐标分别是、 , 点与点关于该函数图象的对称轴对称,求的度数.