第四章《一次函数》培优卷一北师大版(2024)数学八(上)单元分层测

试卷更新日期：2025-10-23 类型：单元试卷

进入出卷网下载

一、单选题（每题3分，共24分）

1. 在同一坐标系中，对于以下几个函数① $y = - x - 1$ ；② $y = x + 1$ ；③ $y = - x + 1$ 　④ $y = - 2 (x + 1)$ 的图象有四种说法（1）过点 $(- 1 ， 0)$ 的是①和③；（2）②和④的交点在y轴上；（3）互相平行的是①和③；（4）关于x轴对称的是②和③．那么正确说法的个数是( )

A、4个 B、3个 C、2个 D、1个

查看试题解析
2. 一次函数y=ax+b与y=abx在同一个平面直角坐标系中的图象不可能是(　　)

A、 B、 C、 D、

查看试题解析
3. 材料：甲开汽车，乙骑自行车从 $A$ 地沿一条笔直的公路匀速前往 $B$ 地，乙比甲先出发．设乙行驶的时间为 $t (h)$ ，甲，乙两人之间的距离 $y (km)$ 关于时间 $t (h)$ 的函数图象如图所示．根据材料，获得正确的信息是（）

A、甲行驶的速度是 $20 km / h$ B、在甲出发 $\frac{3}{2} h$ 后追上乙 C、 $A$ ， $B$ 两地之间的距离为 $90 km$ D、甲比乙少行驶2小时

查看试题解析
4. 有一块长方形菜园 $A B C D$ ，一边利用足够长的墙，另三边用长度为 $20 m$ 的篱笆围成，设长方形的长 $B C$ 为 $x$ $m$ ，宽 $A B$ 为 $y$ $m$ ，则下列函数图象能反映 $y$ 与 $x$ 关系的是 $($ $)$

A、 B、 C、 D、

查看试题解析
5. 如图，在直角坐标系中，一直线与两坐标轴的正半轴分别交于A，B两点，P是线段AB上任意一点(不包括端点)，过点P分别作两坐标轴的垂线，与两坐标轴围成的长方形的周长为8，则该直线的函数表达式是( ).

A、y=-x+4 B、y=x+4 C、y=x+8 D、y=-x+8

查看试题解析
6. 如图，在平面直角坐标系中，点 $A$ 的坐标为 $(0, 3)$ ， $△ O A B$ 沿 $x$ 轴向右平移后得到 $△ O^{^{'}} A^{^{'}} B^{^{'}}$ ，点 $A$ 的对应点 $A^{'}$ 在直线 $y = \frac{3}{4} x$ 上，则点 $B$ 与其对应点 $B^{'}$ 之间的距离（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、3 D、4

查看试题解析
7. 如图，已知 $P (3, 2)$ ， $B (- 2, 0)$ ，点 $Q$ 从 $P$ 点出发，先移动到 $y$ 轴上的点 $M$ 处，再沿垂直于 $y$ 轴的方向向左移动1个单位至点 $N$ 处，最后移动到点 $B$ 处停止.当点 $Q$ 移动的路径最短时 (即三条线段 $P M$ 、 $M N$ 、 $N B$ 长度之和最小)，点 $M$ 的坐标为（）

A、 $(0, \frac{1}{2})$ B、 $(0, \frac{2}{3})$ C、 $(0, \frac{4}{3})$ D、 $(0, \frac{4}{5})$

查看试题解析
8. 如图所示，已知直线 $y = - \frac{\sqrt{3}}{3} x + 1$ 与x、y轴交于B、C两点， $A (0, 0)$ ，在 $△ A B C$ 内依次作等边三角形，使一边在x轴上，另一个顶点在 $B C$ 边上，作出的等边三角形分别是第1个 $△ A A_{1} B_{1}$ ，第2个 $△ B_{1} A_{2} B_{2}$ ，第3个 $△ B_{2} A_{3} B_{3}$ ， …则第2024个等边三角形的边长等于（）

A、 $\frac{3}{2^{2024}}$ B、 $\frac{\sqrt{3}}{2^{2024}}$ C、 $\frac{3}{2^{2025}}$ D、 $\frac{\sqrt{3}}{2^{2025}}$

查看试题解析

二、填空题（每题3分，共15分）

9. 已知 $y = (k - 2) x^{| k | - 1} + 2 k - 3$ 是关于x的一次函数，则这个函数的表达式为．

查看试题解析
10. 如图1，一个正方体铁块放置在圆柱形水槽内，现以一定的速度往水槽中注水， $28 s$ 时注满水槽，水槽内水面的高度 $y (c m)$ 与注水时间 $x (s)$ 之间的函数图象如图2所示.如果将正方体铁块取出，又经过秒恰好将水槽注满.

查看试题解析
11. 函数y=(k-2)x+2k+1的图象经过一、二、四象限，则k的取值范围为.

查看试题解析
12. 在如图所示的平面直角坐标系中，点 $P$ 是直线 $y = x$ 上的动点， $A (1 ， 0)$ ， $B (2 ， 0)$ 是 $x$ 轴上的两点，当 $P A + P B$ 取最小值时， $S_{△ A B P} =$ ．

查看试题解析
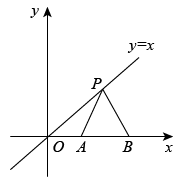13. 如图，在平面直角坐标系中，直线 $y = - \frac{4}{3} x + 4$ 与x轴、y轴分别交于A、B两点，过点B的直线交x轴与点 $C (- 2, 0)$ 若点D在直线 $B C$ 上，且 $△ A C D$ 是以 $A D$ 为腰的等腰三角形，点D的坐标．

查看试题解析

三、解答题（共7题，共61分）

14. 如图①，底面积为30cm² 的空圆柱形容器内水平放置着由两个实心圆柱组成的“几何体”，现向容器内匀速注水，注满为止，在注水过程中，水面高度h(cm)与注水时间t(s)之间的关系如图②所示.请根据图中提供的信息，解答下列问题：

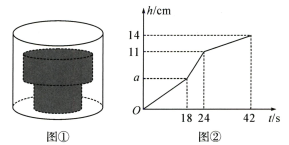(1)、匀速注水的水流速度为cm³/s.

(2)、若“几何体”的下方圆柱的底面积为15cm² ，求“几何体”上方圆柱的高和底面积.

查看试题解析
15. 用一个数对[a ， b]表示从左到右排列的两个数，把[a ， b]变换成[b﹣1，﹣a]称为1次“对调变换”．如：[﹣1，3]经过1次“对调变换”变成[3﹣1，1]，即为[2，1]，再经过1次“对调变换”变成[0，﹣2]．

(1)、把[﹣3，1]先经过1次“对调变换”变成[ ， ]，再连续依次经过3次“对调变换”变成[ ， ]；

(2)、把[a ， b]连续经过2025次“依次变换”变成[﹣2，3]，求a+b的值.

查看试题解析
16. 已知坐标平面上的三个点， $A (0 ， a)$ ， $B (- b, - 1)$ ， $C (b ， 0)$ ，且满足 $\frac{1}{2} \sqrt{7 - a} + |b + 2| = 0$ ．

(1)、求点A，B，C的坐标；

(2)、求 $△ A B C$ 的面积，如图1，若直线 $A B$ 以每秒2个单位的速度向左移，经过多长时间，该直线经过点C．

(3)、如图2， $C D ∥ A B$ ， $∠ D C O$ 的角平分线与 $∠ B A O$ 的补角的角平分线交于点E，求 $∠ E$ 的度数．

查看试题解析
17. 用不同的方式表示同一图形的面积可以解决线段长度的有关问题，这种方法称为等面积法，是一种重要的数学方法．
【问题探究】
数学兴趣小组尝试用等面积法解决下面问题：
如图1，在等腰 $△ A B C$ 中， $A B = A C = 13$ ， $B C = 10$ ， $D$ 是线段 $B C$ 上任意一点，过点 $D$ 作 $D E ⊥ A B$ ， $D F ⊥ A C$ ，垂足分别为 $E$ ， $F$ ．求 $D E + D F$ 的值．
他们用两种方法表示 $△ A B C$ 的面积：
方法一：如图，作 $A G ⊥ B C$ 于点 $G$ ，计算 $△ A B C$ 的面积．
解答过程如下： $\dots$
方法二：连接 $A D$ ，则 $S_{△ A B C} = S_{△ A B D} + S_{△ A C D} = \frac{1}{2} A B \cdot D E + \frac{1}{2} A C \cdot D F$ ．
（1）请将方法一的解答过程补充完整；
（2）结合方法一、二可以算出 $D E + D F =$ 　　．
【学以致用】
如图2，直线 $y = \frac{3}{4} x + \frac{3}{2}$ 与 $x$ 轴交于点 $A$ ，且经过点 $D (2, m)$ ，已知点 $C$ 的坐标为 $(6, 0)$ ．
（1）求直线 $C D$ 的解析式；
（2）在直线 $C D$ 上有一动点 $P$ ，且点 $P$ 到直线 $A D$ 的距离为2，请利用以上所学的知识直接写出点 $P$ 的坐标．

查看试题解析
18. 【定义理解】在平面直角坐标系中，有 $A (m, 0)$ ， $B (0, n)$ 两点，若存在点C使得 $∠ A B C = 90 °$ ，且 $A B = B C$ ，则称点 $C$ 为m的“等垂点”．
例如：在 $A (1, 0)$ ， $B (0, 1)$ ， $C (- 1, 0)$ 三点中，因为 $∠ A B C = 90 °$ ，且 $A B = B C$ ，所以点C为1的“等垂点”．
【探究应用】
（1）点 $A (2, 0)$ ， $B (0, 2)$ ，则 $C (2, 4)$ ____________2的“等垂点”（填“是”或“不是”）．
（2）如图1，若点 $A (4, 0)$ ， $B (0, 3)$ ，则点 $C$ 是4的“等垂点”，则点 $C$ 的坐标为____________．
（3）如图2，若一次函数 $y = 3 x - 5$ 上存在5的“等垂点”，求5的“等垂点”C 的坐标．
【拓展提升】
（4）若在直线 $y = k x + b (k > 0)$ 上存在无数个5的“等垂点”，且直线 $y = k x + b (k > 0)$ 与x轴交于点E，与y轴交于点F，点M在线段 $E F$ 上，点 $P$ 在 $△ E O F$ 内， $E P = 4$ ， $O P = 3$ ，连接 $M P$ ，设 $E M = a$ ，直接写出 $△ E P M$ 面积 $S$ 关于a的表达式．

查看试题解析
19. 材料：如图所示， $B$ 、 $C$ 、 $E$ 三点在同一条直线上， $A C = C D$ ， $∠ B = ∠ E = 90 °$ ， $A C ⊥ C D$ ，则有 $△ A B C ≌ △ C E D$ ．

(1)、【小试牛刀】如图1，在平面直角坐标系中， $O C ⊥ B C$ 且 $O C = B C$ ， $C (1, 4)$ ，点 $C$ 、 $B$ 按顺时针顺序排列，则 $B$ 点坐标为_____________；

(2)、【深入探究】如图2，点 $M$ ， $E$ 分别在 $x$ 轴、 $y$ 轴上， $O M = O E$ ，点 $A$ 在 $x$ 轴负半轴上，连接 $A E$ ，作 $E F ⊥ A E$ 且 $E F = A E$ ，连 $M F$ 交 $y$ 轴于 $N$ ，请猜想线段 $O N$ 与线段 $A M$ 的数量关系并进行证明；

(3)、【拓展提升】如图3， $A (\sqrt{2} + 1, 0)$ ， $A M ⊥ x$ 轴，在直线 $A M$ 上有一动点 $N$ ，连接 $O N$ 并在 $x$ 轴上方作 $O Q ⊥ O N$ 且 $O Q = O N$ ，连接点 $D (\sqrt{2} + 1, \sqrt{2} + 1)$ 与点 $Q$ 的线段平行于 $x$ 轴，连接 $Q N$ 交坐标轴于点 $E$ ，当 $O E = 2$ 时，直接写出 $Q$ 点的坐标．

查看试题解析
20. 为迎接党的二十大，助力乡村振兴，实现群众增产增收，某商场设立专柜，在乡村地区直接采购农副产品，架起对口农户与消费者之间的桥梁，实现农副产品直产直销．该专柜负责人欲查询两种商品的进货数量，发现进货单已被墨水污染．
进货单
商品
进价/（元/件）
数量/件
金额/元
绩溪山核桃
45
黄山毛峰
75
商品采购员李经理对采购情况回忆如下：两种商品共采购了100件．

(1)、若采购花费的总金额为5700元，问绩溪山核桃和黄山毛峰的进货数量分别为多少？

(2)、在进价不变的情况下，由于市场火爆，该专柜负责人计划再次安排采购这两种商品共100件，假设黄山毛峰的进货数量为x（件），所花费的总金额为y（元）．
①求出y与x的函数关系式；
②若李经理用不超过5000元采购这两种商品，问他最多能购买黄山毛峰多少件？

(3)、若绩溪山核桃每件的售价为80元，黄山毛峰每件的售价为100元，商场规定黄山毛峰的进货数是为a（35≤a≤40）件，请问应怎样进货才能使商场在销售完这批货物时获利最多？此时利润为多少元？

查看试题解析

商品	进价/（元/件）	数量/件	金额/元
绩溪山核桃	45
黄山毛峰	75