第四章《一次函数》提升卷一北师大版数学八(上)单元分层测

试卷更新日期：2025-10-23 类型：单元试卷

进入出卷网下载

一、选择题(本大题共8小题，每小题3分，共24分，每小题有四个选项，其中只有一个是正确的)

1. 某市储运部紧急调拨一批物资，调进物资共用4小时，调进物资2小时后开始调出物资(调进物资与调出物资的速度均保持不变).储运部库存物资s(吨)与时间t(小时)之间的函数关系如图所示，这批物资从开始调进到全部调出所需要的时间是( ).

A、4 小时 B、4.4 小时 C、4.8小时 D、5 小时

查看试题解析
2. 函数 $y = \frac{x - 2}{x + 2}$ 的自变量x的取值范围是( ).

A、x>-2 B、x<-2 C、x≠2 D、x≠-2

查看试题解析
3. 在弹性限度内，弹簧伸长的长度与所挂物体的质量成正比 $.$ 某弹簧不挂物体时长 $15 c m$ ；当所挂物体质量为 $3 k g$ 时，弹簧长 $16.8 c m .$ 则弹簧长度 $y (c m)$ 与所挂物体质量 $x (k g)$ 之间的函数表达式为（）

A、 $y = - 0.6 x + 15$ B、 $y = 0.6 x - 15$ C、 $y = - 0.6 x - 15$ D、 $y = 0.6 x + 15$

查看试题解析
4. 函数① $y = 5 x$ ；② $y = 2 x - 1$ ；③ $y = \frac{3}{x}$ ；④ $y = \frac{1}{3} x + 3$ ；⑤ $y = x^{2} - 2 x + 1$ ，是一次函数的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 某品牌的自行车链条每节长为 $2.5 c m$ ，每两节链条相连部分重叠的圆的直径为 $0.8 c m$ ，按照这种连接方式， $n$ 节链条总长度为 $y c m$ ，则 $y$ 与 $n$ 的关系式是（）

A、 $y = 2.5 n$ B、 $y = 1.7 n$ C、 $y = 1.7 n + 0.8$ D、 $y = 2.5 n - 0.8$

查看试题解析
6. 若 abc<0，直线 $y = \frac{a}{b} x - \frac{c}{a}$ 不经过第四象限，则直线y=(a+b)x+c一定不经过( ).

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 对于一次函数 $y = - x + 3$ 的相关性质，下列描述错误的是（）

A、函数图象经过第一、二、四象限 B、函数图象与x轴的交点坐标为 $(0, 3)$ C、y随x的增大而减小 D、函数图象与坐标轴围成的三角形面积为 $\frac{9}{2}$

查看试题解析
8. 某条公共汽车线路收支差额 $y$ 与乘客量 $x$ 的函数关系如图所示（收支差额 $=$ 车票收入 $-$ 支出费用），由于目前本条线路亏损，公司有关人员提出了两条建议：建议(Ⅰ)不改变支出费用，提高车票价格；建议(Ⅱ)不改变车票价格，减少支出费用.下面给出的四个图形中，实线和虚线分别表示目前和建议后的函数关系，则下列说法正确的是：

A、①反映了建议（Ⅱ），③反映了建议（Ⅰ） B、②反映了建议（Ⅰ)，④反映了建议（Ⅱ） C、①反映了建议（Ⅰ），③反映了建议（Ⅱ） D、②反映了建议（Ⅱ），④反映了建议（Ⅰ）

查看试题解析

二、填空题(本大题共5小题，每小题3分，共15分)

9. 某市居民生活用水的价格是2.9元/立方米。设某户居民这个月的用水量为n立方米，应付水费为m元。在这个问题中，m关于n的函数表达式是。当n=15时，函数值是，这一函数值的实际意义是。

查看试题解析
10. 已知 $y = (m - 6) x^{m^{2} - 35} + 10$ 是关于x的一次函数，则 $m =$ ．

查看试题解析
11. 如图，在平面直角坐标系中，一次函数y=2x-1的图象分别交x轴、y轴于点A，B，将直线AB 绕点 B 按顺时针方向旋转45°，交x轴于点 C，则直线BC 的函数表达式是.

查看试题解析
12. 如图，在平面直角坐标系 $x O y$ 中，点 $A$ 的坐标为 $(0, 4)$ ，点 $B$ 在第一象限内，将 $△ O A B$ 沿 $x$ 轴正方向平移得到 $△ O' A' B'$ ，若点 $A$ 的对应点 $A'$ 在直线 $y = \frac{4}{5} x$ 上，则点 $B$ 与其对应点 $B'$ 之间的距离为.

查看试题解析
13. 已知直线 $y = \frac{1}{3} x + 2$ 与函数 $y = \{\begin{matrix} x + 1 (x \geq - 1) \\ - x - 1 (x < - 1) \end{matrix}$ 的图像相交于 $A, B$ 两点（点 $A$ 在点 $B$ 左侧）．
（1）点 $B$ 的坐标是．
（2）若坐标原点为点 $O$ ，将两个函数图象向右平移 $m$ 个单位，点 $A, B$ 平移后分别对应点 $C, D$ ，连接 $O C, O D$ ，当 $|O C - O D|$ 最大时， $m$ 的值为．

查看试题解析

三、解答题（共7题，共61分）

14. 小明在游乐场坐过山车，某一分钟内过山车高度h（米）与时间 $t$ （秒）之间的函数图象如图所示，请结合图象回答：

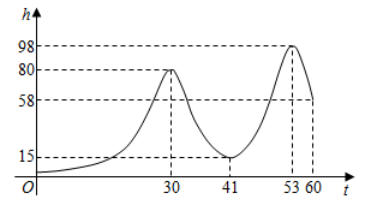(1)、过山车所达到的最大高度是多少？

(2)、请描述 $41$ 秒后，高度 $h$ （米）随时间 $t$ （秒）的变化情况

查看试题解析
15. 周末，小丽和爸爸、妈妈一家三口去杨梅园游玩．已知该杨梅园内的杨梅单价是每千克40元．为满足客户需求，该杨梅园现推出两种不同的销售方案：
甲方案：游客进园需购买30元的门票，采摘的杨梅按原价的六折收费；
乙方案：游客进园不需购买门票，采摘的杨梅在10千克以内按原价收费、超过10千克后，10千克部分按原价收费，超过部分按原价的五折收费．
设采摘量为x千克，按甲方案所需总费用为 $y_{1}$ 元，按乙方案所需总费用为 $y_{2}$ 元．

(1)、当采摘量超过10千克时，分别求出 $y_{1}$ 、 $y_{2}$ 关于x的函数表达式；

(2)、若采摘量为30千克，选择哪种方案更划算？请说明理由．

查看试题解析
16. 已知关于x的函数 $y = (m + 1) x + (m^{2} - 1) .$

(1)、当m取什么值时，y是x的一次函数?

(2)、当m取什么值时，y是x的正比例函数?

(3)、当m取什么值时，该函数与函数y=-x+3是同一个函数?

查看试题解析
17. 定义：在平面直角坐标系中，将直线 $l_{1} : y = a x + b$ $(a b \neq 0)$ 中a和b的值都扩大到原来的 $k (k > 0)$ 倍，得到新的直线 $l_{2}$ ，则称直线 $l_{2}$ 为直线 $l_{1}$ 的“k倍伴随线”，例如直线 $y = 4 x + 3$ 的“2倍伴随线”的函数解析式为 $y = 8 x + 6$ ．

(1)、求直线 $y = 2 x + 3$ 的“3倍伴随线”的函数表达式；

(2)、若点 $(m, - 10)$ 在直线 $y = x - 6$ 的“2倍伴随线”上，求m的值．

查看试题解析
18. 在平面直角坐标系xOy中，点 P 的坐标为(m+1，m-1).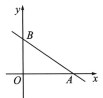

(1)、试判断点 P 是否在一次函数y=x-2的图象上，并说明理由.

(2)、如图，一次函数 $y = - \frac{1}{2} x + 3$ 的图象与x轴、y轴分别相交于点A，B，若点 P 在△AOB 的内部，求 m 的取值范围.

查看试题解析
19. 阅读下面材料，再回答问题．
一般地，如果函数y=f（x）对于自变量取值范围内的任意x，都有f（﹣x）=f（x）．那么y=f（x）就叫偶函数．如果函数y=f（x）对于自变量取值范围内的任意x，都有f（﹣x）=﹣f（x）．那么y=f（x）就叫奇函数．
例如：f（x）=x⁴
当x取任意实数时，f（﹣x）=（﹣x）⁴=x⁴∴f（﹣x）=f（x）∴f（x）=x⁴是偶函数．
又如：f（x）=2x³﹣x．
当x取任意实数时，∵f（﹣x）=2（﹣x）³﹣（﹣x）=﹣2x³+x=﹣（2x³﹣x）∴f（﹣x）=﹣f（x）∴f（x）=2x³﹣x是奇函数．

(1)、问题1：下列函数中：①y=x²+1② $y = \frac{5}{x^{3}}$ ③ $y = \sqrt{x + 1}$ ④ $y = x + \frac{1}{x}$ ⑤y=x^﹣²﹣2|x|
是奇函数的有；是偶函数的有（填序号）

(2)、问题2：仿照例证明：函数④或⑤是奇函数还是偶函数（选择其中之一）

查看试题解析

20. 葡萄是本地区重要农业经济产业，种植葡萄能增加农民的收入.根据提供的材料解决问题.

项目	内容
材料一	某商贸公司经销甲、乙两个品种的葡萄，甲种葡萄进价为5元/斤；乙品种葡萄的进货总金额 $y$ （单位：元）与乙品种葡萄的进货量 $x$ （单位：斤）之间的关系如图所示.经过试销，在 $H$ 城市销售甲、乙两个品种薄萄的售价分别为7元/斤和14元/斤.
材料二	在葡萄节开节当日，该商贸公司收购了甲、乙两个品种的葡萄共20000斤，其中乙品种的收购量不低于4000斤，且不高于10000斤.
材料三	葡萄运到H城市，商场发现顾客对甲、乙两个品种葡萄都很喜欢，于是决定把两种葡萄进行混合销售，并适当让利给消费者.

(1)、求图中直线

M N

函数解析式.

(2)、若从收购点运到商场的其他各种费用还需要18000元，收购的葡萄能够全部卖完，设销售完甲、乙两个品种的葡萄所获总利润为

w

元（利润＝销售额－成本）.求出

w

（单位：元）与乙品种葡萄的进货量

x

（单位：斤）之间的函数关系式，并为该商贸公司设计出获得最大利润的收购方案.

(3)、在任务二获得的最大利润的基础上，商场把最大利润的

\frac{1}{3}

让利给购买者，那么混合销售葡萄的销售价应定为多少？

查看试题解析