人教版七年级上同步分层训练6.3角

试卷更新日期：2025-10-22 类型：同步测试

进入出卷网下载

一、夯实基础

1. 如图，用量角器度量几个角的度数，下列结论正确的有（）
① $∠ B O C = 60 °$ ；② $∠ A O D$ 与 $∠ B O C$ 互补；③ $∠ A O B = ∠ D O E$ ；④ $∠ A O B$ 是 $∠ D O E$ 的余角；⑤ $O C$ 平分 $∠ B O D$ ．

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 如图所示，下列表示角的方法中，错误的是( )

A、∠1与∠AOB表示同一个角 B、∠β表示的是∠BOC C、∠AOC也可用∠O来表示 D、图中共有三个角，分别是∠AOB，∠AOC，∠BOC

查看试题解析
3. 下面等式成立的是（）

A、 $83.5 ° = 83 ° 50'$ B、 $90 ° - 57 ° 23' 27'' = 32 ° 37' 33''$ C、 $15 ° 48' 36'' + 37 ° 27' 59'' = 52 ° 16' 35''$ D、 $41.25 ° = 41 ° 15'$

查看试题解析
4. 如图， $∠ A O B = ∠ C O D = 90 °$ ，下列结论：① $∠ A O C + ∠ B O D = 90 °$ ；②图中 $∠ B O C$ 有两个余角；③若 $O C$ 平分 $∠ A O B$ ，则 $O B$ 平分 $∠ C O D$ ；④ $∠ A O D$ 的平分线平分 $∠ C O B$ ．其中正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
5. 下列结论中，错误的是( )

A、一个角的补角一定大于这个角 B、已知一个角的度数为 $54 ° 11^{'} 23^{'}' ，$ 则它的补角的度数为 125°48'37" C、若 $∠ 1 + ∠ 2 = 90 ° ， ∠ 1 + ∠ 3 = 90 ° ，$ 则∠2=∠3 D、已知一个角的余角是这个角的2倍，则这个角是30°

查看试题解析
6. 如图，在灯塔0处观测到轮船A位于北偏西 60°的方向，轮船B在南偏东 20°的方向则∠AOB的大小为.

查看试题解析
7. 如图点O在直线 BD上，已知∠COD=95°，AO⊥CO，则∠AOB 的度数为。

查看试题解析
8. 如图，点 $O$ 为直线 $A B$ 上一点，过点 $O$ 作射线 $O C$ ，使 $∠ A O C = 60 °$ ，射线 $O P$ 与 $O C$ 位于直线 $A B$ 同侧， $O M$ 平分 $∠ C O P$ ．

(1)、如图，当 $∠ B O P = 10 °$ 时，求 $∠ A O M$ 的度数．

(2)、若 $∠ A O M = 2 ∠ B O P$ ，通过计算判断 $∠ C O M$ 与 $∠ B O P$ 的大小关系，并说明理由．

查看试题解析
9. 如图，直线 $A B$ 和 $C D$ 交于点O， $∠ C O E = 90 °$ ， $O D$ 平分 $∠ B O F$ ， $∠ B O E = 55 °$ ．

(1)、求 $∠ A O C$ 的度数；

(2)、求 $∠ E O F$ 的度数．

查看试题解析

二、能力提升

10. 如图，O为直线AB 上一点，∠DOC 为直角，OE 平分∠BOC，OF 平分∠AOD，OG 平分∠AOC.下列结论：①∠BOE 与∠DOF 互为余角；②2∠AOE-∠BOD=90°；③∠EOD 与∠COG 互为补角；④∠BOE-∠DOF=45°.其中结论正确的是( )

A、①②④ B、③④ C、②③ D、②③④

查看试题解析
11. 如图， $∠ A O B = 120 °$ ，在 $∠ A O B$ 内作两条射线 $O C$ 和 $O D$ ，且 $O M$ 平分 $∠ A O D ， O N$ 平分 $∠ B O C$ ，若 $∠ A O C : ∠ C O D : ∠ D O B = 5 : 3 : 4$ ，则 $∠ M O N$ 的度数为（　　）

A、 $45 °$ B、 $50 °$ C、 $55 °$ D、 $60 °$

查看试题解析
12. 上午 $6 ： 50$ 时，钟表的分针与时针夹角的度数是（）

A、105度 B、85度 C、95度 D、115度

查看试题解析
13. 如果 $∠ α$ 和 $∠ β$ 互余，则下列式子中表示 $∠ α$ 补角是（）
①180°－ $∠ α$ ；② $∠ α$ ＋2 $∠ β$ ；③2 $∠ α$ ＋ $∠ β$ ；④ $∠ β$ ＋90°

A、①②④ B、①②③ C、①③④ D、②③④

查看试题解析
14. 如图，两个正方形的一个顶点互相重合，且重合的顶点在一条直线上，那么∠1的度数为.

查看试题解析
15. 如图，已知∠AOB=∠COD=90°，∠COE=∠BOE，点 F 为OE 反向延长线上一点（图中所有角均指小于180°的角），给出下列结论：
①∠AOE=∠DOE；②∠AOD+∠COB=180°；③∠COB-∠AOD=90°；④∠COE+∠BOF=180°.
其中结论正确的是.

查看试题解析
16. 如图，射线OC，OD，OE，OF 分别平分∠AOB，∠COB，∠AOC，∠EOC.若∠FOD=24°，则∠AOB=.

查看试题解析
17. 已知直线 $A B$ 经过点O， $∠ C O D = 90 °$ ， $O E$ 是 $∠ B O C$ 的平分线．

(1)、如图1，若 $∠ A O C = 30 °$ ，求 $∠ D O E$ ；

(2)、如图1，若 $∠ A O C = α$ ，求 $∠ D O E$ ；（用含 $α$ 的式子表示）

(3)、将图1中的 $∠ C O D$ 绕顶点O顺时针旋转到图2的位置，其它条件不变，（2）中的结论___________（填“成立”或“不成立”）；

(4)、将图1中的 $∠ C O D$ 绕顶点O逆时针旋转到图3的位置，其它条件不变，求（2）中的结论是否还成立？试说明理由．

查看试题解析

三、拓展创新

18. 如图，射线 OB，OC分别在∠AOD，∠BOD的内部，且射线OM，ON分别平分∠AOB，∠COD。若∠MON=a，∠BOC=B，则∠AOD=（）

A、2a B、2a-β C、a+β D、a-β

查看试题解析
19. 如图①，O为直线AB 上一点，作射线OC，使 $∠ A O C ： ∠ B O C =$ 2：1，将一把直角三角尺如图摆放，直角顶点在点O处，一条直角边OP 在射线OA 上.将图①中的三角尺绕点O以每秒5°的速度按逆时针方向旋转(如图②所示)，在旋转一周的过程中，第t秒时，OQ所在直线恰好平分∠AOC，则t的值为.

查看试题解析
20. 已知：O是直线AB 上的一点，∠COD 是直角，OE 平分∠BOC.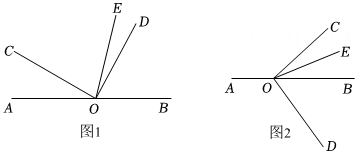

(1)、如图①，若∠AOC=30°，求∠DOE 的度数.

(2)、在图①中，若∠AOC=α，直接写出∠DOE 的度数（用含α的代数式表示）.

(3)、将图①中的∠COD 绕顶点O 顺时针旋转至图②的位置.
①探究∠AOC 与∠DOE 的度数之间的关系；
②在 $∠ A O C$ 的内部有一条射线OF，满足∠AOC—4∠AOF= $2 ∠ B O E + ∠ A O F,$ ，试确定∠AOF 与∠DOE 的度数之间的关系，并说明理由.

查看试题解析

21.

信息1

小刚和小颖两家人分别开车匀速行驶在笔直的高速公路上（如图1），小颖家车的速度是100千米/时，小刚家车的速度是小颖家车的速度的1.2倍，将车看成点，高速公路看成直线，得到图2的示意图，甲表示小刚家的车，乙表示小颖家的车．

信息2

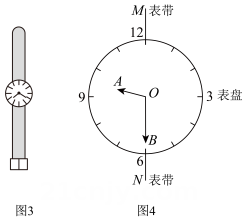
某时刻乙车在甲车前方20千米，此时小刚看到自己手表（图3）显示的时间如图4中表盘所示，OA表示时针，OB表示分针，时针和分针在转动的过程中形成的角是∠AOB（0°<∠AOB<180°），表带所在直线为MN ．

根据以上信息回答问题：

(1)、小刚看表时，时针OA和分针OB的夹角∠AOB为°．

(2)、①经过小时，甲车追上乙车；

②甲车刚追上乙车时，此时时针OA和分针OB的夹角∠AOB为°．

(3)、①在表盘中分针OB每分钟转过°，时针OA每分钟转过°；

②自小刚看表时刻开始，到甲车追上乙车时这段时间之内，经过分钟后，∠AOB的度数是90° ．

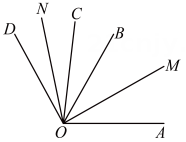
(4)、小刚根据时针和分针的启示，做了一个类似的装置（如图5），该装置的“表带”所在直线是MN ，装置有三根指针分别为OD、OE和OF ，指针OEOF在转动过程中保持∠EOF=90°，指针OD始终平分∠FON ，指针OF从图5所示位置（OF和射线ON重合）以每秒6°顺时针开始旋转，经过t秒后（0<t<15），OF转到图6位置时，小刚记下此时∠EOD=x°，继续转动m秒（0<m<15），当OF转到图7位置时，小刚记下此时∠EOD=y°，若x-y=21，直接写出m的值

查看试题解析