人教版七(上)第三章 代数式 单元测试培优卷
试卷更新日期:2025-10-21 类型:单元试卷
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1. 下列各式中,代数式有( )
;;;;;;;.
A、5个 B、6个 C、7个 D、8个2. 大约从 20 世纪 50 年代开始,许多国家流传着这样一个数学猜想,其原理如下图数值转换器。若开始输入 的值是 5 ,则第 1 次输出的结果是 16 ,第 2 次输出的结果是 8 ,第 3 次输出的结果是 4 .依次继续下去,第 2025 次输出的结果是( ) A、1
A、1
B、2
C、3 D、43. 用下列各式分别表示下面几何图形的面积,其中表示正确的有( )①②
③ ④
 A、4个 B、3个 C、2个 D、1个4. 若 , 且 , 则式子的值等于( )A、7 B、1 C、1或 D、5或5. 已知是一个两位数,也是一个两位数,将放在的左边构成一个新的四位数,则这个四位数可以表示为( )A、 B、 C、 D、6. 若时,式子的值为2025,则当时,式子的值为( )A、 B、 C、 D、7. 观察下面三行数:
A、4个 B、3个 C、2个 D、1个4. 若 , 且 , 则式子的值等于( )A、7 B、1 C、1或 D、5或5. 已知是一个两位数,也是一个两位数,将放在的左边构成一个新的四位数,则这个四位数可以表示为( )A、 B、 C、 D、6. 若时,式子的值为2025,则当时,式子的值为( )A、 B、 C、 D、7. 观察下面三行数:, 9, , 81……①
1, , 9,……②
, 10, , 82……③
设x,y,z分别为第①②③行的202个数,则的值为( )
A、1 B、 C、 D、8. 9月16号,杭州亚运村举行开村仪式暨中国体育代表团欢迎仪式,有位运动员乘坐辆车,若每辆车载人,则还有人不能上车;若每辆车载人,则最后一辆车空了个座位.①运动员有人;②运动员有人;③运动员乘坐的车有辆;④运动员乘坐的车有辆.其中正确的是( )A、①②③ B、①②④ C、①③④ D、②③④9. 如图:圆,三角形,正方形三个图形的面积相等,重叠部分面积分别记为和 , 不重叠部分面积分别记为 , , , , 若 , 则 , , , 之间的数量关系为( ) A、 B、 C、 D、10. 如图,各正方形中的四个数之间都有相同的规律,根据此规律,x的值为( )
A、 B、 C、 D、10. 如图,各正方形中的四个数之间都有相同的规律,根据此规律,x的值为( ) A、220 B、232 C、242 D、252
A、220 B、232 C、242 D、252二、填空题:本大题共5小题,每小题3分,共15分.
-
11. 甲、乙两地相距千米,某人用小时从甲地骑行到乙地,再开车回到甲地,总用时小时,那么他开车的平均速度为千米/时.12. 已知 , 则的值为 .13. 如图是用三角形摆成的图案,摆第一层图案需要1个三角形,摆第二层图案需要3个三角形,摆第三层图案需要7个三角形,摆第四层图案需要13个三角形,摆第10层图案需要个三角形,……,摆第层图案需要个三角形.
 14. “低多边形风格”是一种数字艺术设计风格,它将整个区域分割为若干三角形,通过把相邻三角形涂上不同颜色,产生立体和光影效果.将长方形区域分割成三角形的过程是:在长方形内取一定数量的点,连同长方形的4个顶点,逐步连接这些点,保证所有连线不再相交产生新的点,直到长方形内所有区域都变成三角形.若长方形内有4个点,则三角形个数为个,若长方形内有个点,则三角形个数为个(不计被分割的三角形).
14. “低多边形风格”是一种数字艺术设计风格,它将整个区域分割为若干三角形,通过把相邻三角形涂上不同颜色,产生立体和光影效果.将长方形区域分割成三角形的过程是:在长方形内取一定数量的点,连同长方形的4个顶点,逐步连接这些点,保证所有连线不再相交产生新的点,直到长方形内所有区域都变成三角形.若长方形内有4个点,则三角形个数为个,若长方形内有个点,则三角形个数为个(不计被分割的三角形). 15. 如图,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第20个图需要黑色棋子的个数为 .
15. 如图,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第20个图需要黑色棋子的个数为 .
三、解答题:本大题共8小题,共75分.
-
16. 李华家中有一个长方形窗户(如图),窗帘是由半径相同的两个四分之一圆组成的,图中透光面积(空白部分的面积)为 .
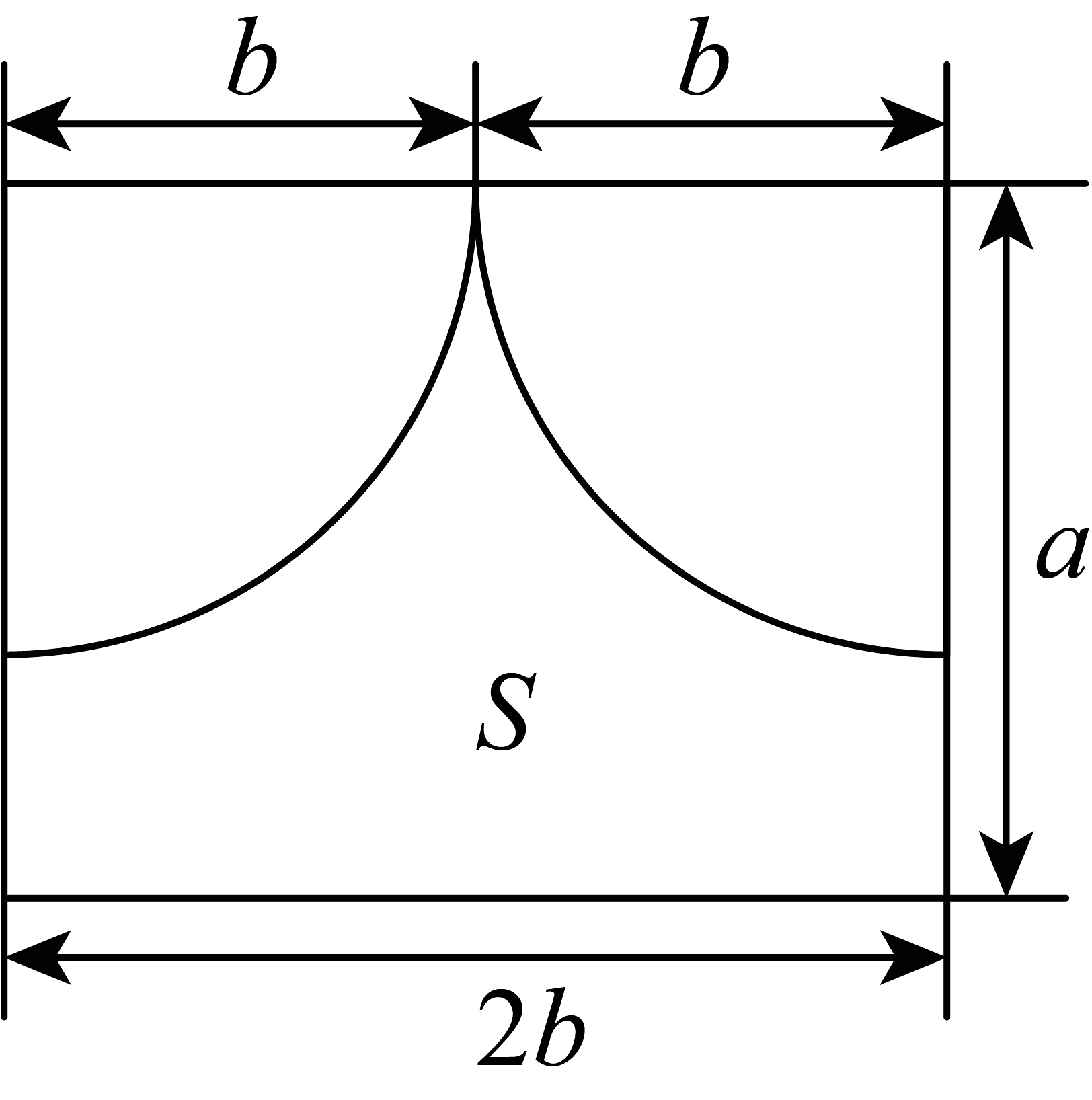 (1)、请用含、的代数式表示;(2)、当 , 时,的值.(取).17. 用三角形和六边形按如图所示的规律拼图案.
(1)、请用含、的代数式表示;(2)、当 , 时,的值.(取).17. 用三角形和六边形按如图所示的规律拼图案. (1)、第5个图案中,三角形有个,六边形有个.(2)、第为正整数个图案中,三角形与六边形各有多少个?(3)、是否存在某个符合上述规律的图案,其中有100个三角形和40个六边形?如果存在,指出是第几个图案;如果不存在,请说明理由.18. 如图,正方形的边长为x.
(1)、第5个图案中,三角形有个,六边形有个.(2)、第为正整数个图案中,三角形与六边形各有多少个?(3)、是否存在某个符合上述规律的图案,其中有100个三角形和40个六边形?如果存在,指出是第几个图案;如果不存在,请说明理由.18. 如图,正方形的边长为x. (1)、根据图中数据,用含x,y的代数式表示阴影部分的面积S;(2)、当 , 时,求阴影部分的面积.19. 为了调动学生们体育锻炼的积极性,学校准备订购一批篮球和跳绳,经过市场调查后发现篮球每个定价120元,跳绳每条定价20元.某体育用品商店提供A,B两种优惠方案方案:买一个篮球送一条跳绳;B方案:篮球和跳绳都按定价的付款.已知要购买篮球50个,跳绳条.(1)、若按A方案购买,一共需付款元;若按B方案购买,一共需付款元.(用含的代数式表示)(2)、当时,请通过计算说明此时用哪种方案购买较为合算?(3)、当时,你能给出一种更为省钱的购买方案吗?请写出你的购买方案,并计算需付款多少元?20. 某大型商场销售一种茶具和茶碗,茶具每套定价200元,茶碗每只定价20元.“双十一”期间商场决定开展促销活动,活动期间向客户提供优惠方案如下:
(1)、根据图中数据,用含x,y的代数式表示阴影部分的面积S;(2)、当 , 时,求阴影部分的面积.19. 为了调动学生们体育锻炼的积极性,学校准备订购一批篮球和跳绳,经过市场调查后发现篮球每个定价120元,跳绳每条定价20元.某体育用品商店提供A,B两种优惠方案方案:买一个篮球送一条跳绳;B方案:篮球和跳绳都按定价的付款.已知要购买篮球50个,跳绳条.(1)、若按A方案购买,一共需付款元;若按B方案购买,一共需付款元.(用含的代数式表示)(2)、当时,请通过计算说明此时用哪种方案购买较为合算?(3)、当时,你能给出一种更为省钱的购买方案吗?请写出你的购买方案,并计算需付款多少元?20. 某大型商场销售一种茶具和茶碗,茶具每套定价200元,茶碗每只定价20元.“双十一”期间商场决定开展促销活动,活动期间向客户提供优惠方案如下:方案一:买一套茶具送一只茶碗;
方案二:茶具和茶碗按定价的九五折付款.
现在某客户要到商场购买茶具30套,茶碗x只 .
(1)、用含x的代数式分别表示方案一和方案二的应付钱数;(2)、若 , 选择上述两个方案中的一个,则选择哪个比较省钱?请计算说明;(3)、当 , 能否找到一种更为省钱的方案,如果能,写出你的方案,并计算出此方案应付钱数;如果不能,请说明理由.21. 如图是由边长相同的灰、白方块拼成的图形. (1)、请观察图形,并填写下列表格;
(1)、请观察图形,并填写下列表格;图形标号
第1个
第2个
第3个
…
第n个
灰色方块的个数
5
10
15
…
______
白色方块的个数
4
______
______
…
______
(2)、第100个图形中的灰色方块和第102个图形中的白色方块共有多少个?(3)、第个图形中的灰色方块比第个图形中的白色方块多多少个?(用含n的式子表示)22. 现有a根长度相同的火柴棒,按图(1)可摆成m个正方形,按图(2)可摆成个正方形.
(1)用含n的代数式表示m;
(2)当这a根火柴棒还能摆成如图(3)所示的形状时,求a的最小值.
23. 关于x的代数式,当x取任意一组相反数a与时,若代数式的值相等,则称之为“偶代数式”;若代数式的值互为相反数,则称之为“奇代数式”,例如代数式是“偶代数式”,是“奇代数式”.(1)、以下代数式中,是“偶代数式”的有_______,是“奇代数式”的有________;(将正确选项的序号填写在横线上.①;②;③ .
(2)、某个奇代数式,当x取2时,代数式的值为3,问:当x取时,代数式的值为多少?(3)、对于整式 , 当x分别取 , , , , 0,1,2,3,4时,这九个整式的值之和是_______.