人教版八(上)第十五章 轴对称单元测试培优卷
试卷更新日期:2025-10-21 类型:单元试卷
一、选择题
-
1. 下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若等腰三角形有一个角是 100°,则它的底角为( )A、100° B、40° C、100°或 40° D、80°3. 如图,在方格纸上,A,B是格点,网格中存在格点C使得是以为顶角的等腰三角形,这样的格点C的个数为( )
2. 若等腰三角形有一个角是 100°,则它的底角为( )A、100° B、40° C、100°或 40° D、80°3. 如图,在方格纸上,A,B是格点,网格中存在格点C使得是以为顶角的等腰三角形,这样的格点C的个数为( ) A、4 B、5 C、6 D、74. 如图,在中,的垂直平分线分别交、于点、 , 的垂直平分线分别交、于点、 . 若 , 则的度数是( )
A、4 B、5 C、6 D、74. 如图,在中,的垂直平分线分别交、于点、 , 的垂直平分线分别交、于点、 . 若 , 则的度数是( ) A、 B、 C、 D、5. 如图,在中, , , 点D是的中点,过点D作交于点E, , 则的长度为( )
A、 B、 C、 D、5. 如图,在中, , , 点D是的中点,过点D作交于点E, , 则的长度为( ) A、7 B、8 C、9 D、106. 如图,在中, , , 分别以 , 两点为圆心,大于为半径画弧,两弧交于 , 两点,直线交于点 , 交于点 , 若 , 则的长度为( )
A、7 B、8 C、9 D、106. 如图,在中, , , 分别以 , 两点为圆心,大于为半径画弧,两弧交于 , 两点,直线交于点 , 交于点 , 若 , 则的长度为( ) A、6 B、7 C、8 D、97. 如图,是等边三角形,D、E分别是的边、上的点,且 , 与相交于点P,于点F, , , 则的长为( )
A、6 B、7 C、8 D、97. 如图,是等边三角形,D、E分别是的边、上的点,且 , 与相交于点P,于点F, , , 则的长为( ) A、8 B、13 C、16 D、178. 如图, , P是它内部一点, , , 分别是 , 上的两个动点,则的最小值是( )
A、8 B、13 C、16 D、178. 如图, , P是它内部一点, , , 分别是 , 上的两个动点,则的最小值是( ) A、 B、 C、 D、9. 如图,在中,分别为边上的高,相交于点 , , 连接 , 则下列结论:①;②;③;④若 , 则周长等于的长.其中正确的有( )
A、 B、 C、 D、9. 如图,在中,分别为边上的高,相交于点 , , 连接 , 则下列结论:①;②;③;④若 , 则周长等于的长.其中正确的有( ) A、①② B、①③ C、①③④ D、②③④10. 如图,点D在△ABC内部,且DA=DB=DC,点E在AB边上,且EB=EC,∠AEC=60°,连接ED并延长交BD于点F.以下结论:①EF⊥BC;②∠BAD+∠BCD=30°;③∠ADC=60°;④AE+DE=BE.其中正确的结论有( )
A、①② B、①③ C、①③④ D、②③④10. 如图,点D在△ABC内部,且DA=DB=DC,点E在AB边上,且EB=EC,∠AEC=60°,连接ED并延长交BD于点F.以下结论:①EF⊥BC;②∠BAD+∠BCD=30°;③∠ADC=60°;④AE+DE=BE.其中正确的结论有( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 如图, 在 中, A C 边的垂直平分线分别交 AC, AB 于点 的周长为 18 cm , 则 的周长为cm .
 12. 如图,已知 , 点在边上, , 点M,N在边上, , 若 , 求的长
12. 如图,已知 , 点在边上, , 点M,N在边上, , 若 , 求的长 13. 如图,为内一点,平分 , , , 若 , , 则的长为 .
13. 如图,为内一点,平分 , , , 若 , , 则的长为 .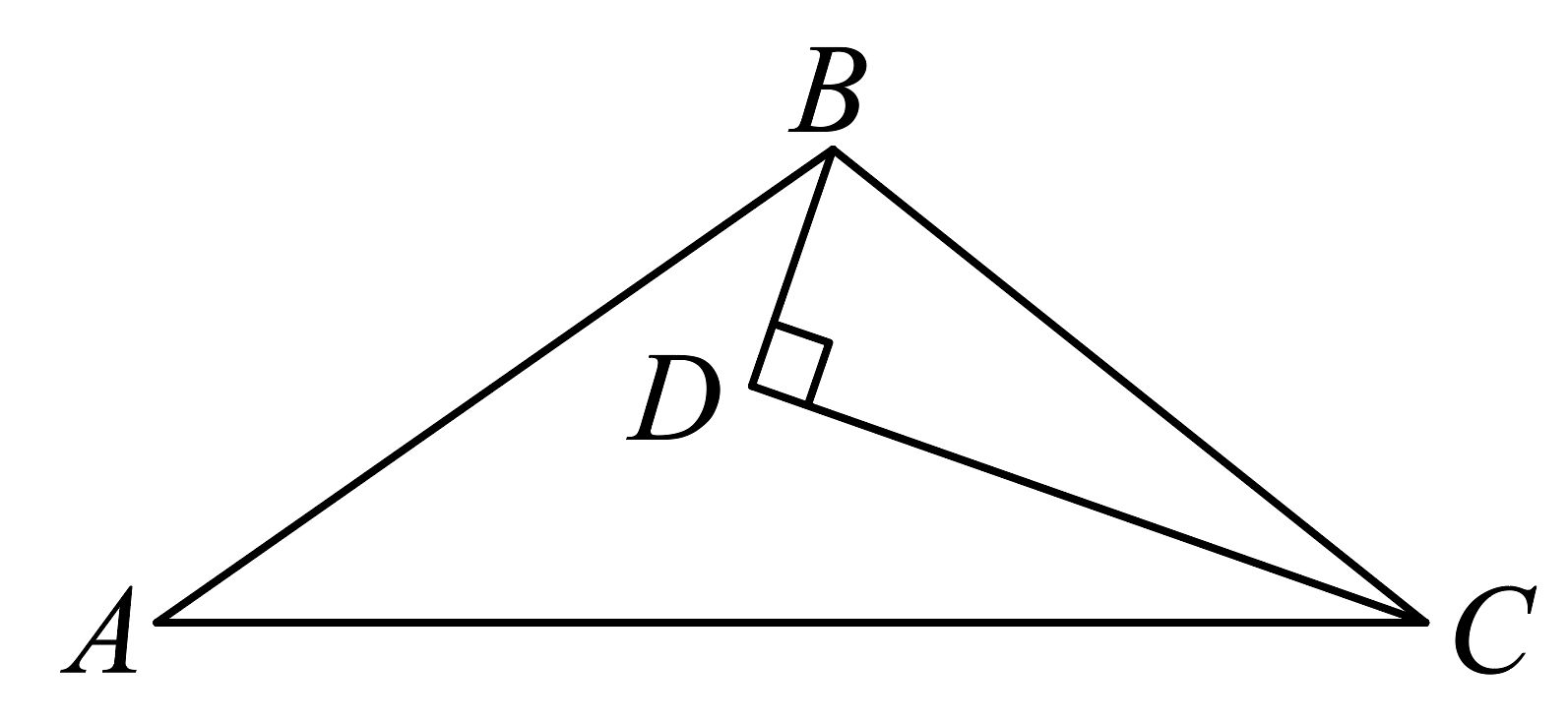 14. 如图,点为内部一点,使得 , , , , 则的度数为 .
14. 如图,点为内部一点,使得 , , , , 则的度数为 . 15. 如图,已知等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面结论:
15. 如图,已知等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面结论:①∠ACO=15°;
②∠APO+∠DCO=30°;
③△OPC是等边三角形;
④AC=AO+AP;其中正确的有 (填上所有正确结论的序号).

三、解答题
-
16. 如图,在平面直角坐标系中,A(0,1),B(﹣2,3),C(4,4).
 (1)、在图中作出△ABC关于x轴的对称图形△A′B′C′;
(1)、在图中作出△ABC关于x轴的对称图形△A′B′C′;
(2)、写出△A′B′C′三个顶点的坐标.17. 如图,在中, , 点是边上的中点,连结 , 平分交于点 , 过点作交于点 . (1)、若 , 求的度数;(2)、求证: .18. 如图,在中,的垂直平分线分别交于点D、E, 的垂直平分线分别交于点F、G.
(1)、若 , 求的度数;(2)、求证: .18. 如图,在中,的垂直平分线分别交于点D、E, 的垂直平分线分别交于点F、G. (1)、若 , 求的周长.(2)、若 , 求的度数.19. 已知:如图,点M在锐角∠AOB的内部,在OA边上求作一点P , 在OB边上求作一点Q , 使得△PMQ的周长最小.
(1)、若 , 求的周长.(2)、若 , 求的度数.19. 已知:如图,点M在锐角∠AOB的内部,在OA边上求作一点P , 在OB边上求作一点Q , 使得△PMQ的周长最小. 20. 如图,在中, , 平分 , 于 , 连接 , 交于点 .
20. 如图,在中, , 平分 , 于 , 连接 , 交于点 . (1)、求证:是线段的垂直平分线;(2)、若 , , 求的长.21. 如图,平分 , P为上的一点,的两边分别与相交于点M、N.
(1)、求证:是线段的垂直平分线;(2)、若 , , 求的长.21. 如图,平分 , P为上的一点,的两边分别与相交于点M、N. (1)、如图1,若 , , 过点P作于点E,作于点F,请判断与的数量关系,并说明理由;(2)、如图2,若 , , 求证: .
(1)、如图1,若 , , 过点P作于点E,作于点F,请判断与的数量关系,并说明理由;(2)、如图2,若 , , 求证: .

