【湖南卷】备战2026年中考数学真题变式阶梯训练第25~26题
试卷更新日期:2025-10-20 类型:二轮复习
一、原题25
-
1. 【问题背景】
如图1,在平行四边形纸片ABCD中,过点B作直线l⊥CD于点E , 沿直线l将纸片剪开,得到△B1C1E1和四边形ABED , 如图2所示.
【动手操作】
现将三角形纸片B1C1E1和四边形纸片ABED进行如下操作(以下操作均能实现)
①将三角形纸片B1C1E1置于四边形纸片ABED内部,使得点B1与点B重合,点E1在线段AB上,延长BC1交线段AD于点F , 如图3所示;
②连接CC1 , 过点C作直线CN⊥CD交射线EE1于点N , 如图4所示;
③在边AB上取一点G , 分别连接BD , DG , FG , 如图5所示.

【问题解决】
请解决下列问题:
(1)、如图3,填空:∠A+∠ABF= °;(2)、如图4,求证:△CNM≌△C1E1M;(3)、如图5,若 , ∠AGD=60°,求证:FG∥BD .二、变式1基础
-
2. 如图,已知平行四边形ABCD,连接对角线AC,BD交于点E,过点E作PQ⊥MN,分别与AB,BC,CD,DA交于点P,M,Q,N.
 (1)、求证:Δ DEQ ≅ Δ BEP . .(2)、若依次连接P,M,Q,N,四边形PMQN是什么特殊四边形?说明理由3. 如图,在▱ABCD中,∠ABC 的平分线 BE 交 AD 于点 E,AF⊥BE 于点 F,延长 AF交 BC于点 G,连结 EG,CF.
(1)、求证:Δ DEQ ≅ Δ BEP . .(2)、若依次连接P,M,Q,N,四边形PMQN是什么特殊四边形?说明理由3. 如图,在▱ABCD中,∠ABC 的平分线 BE 交 AD 于点 E,AF⊥BE 于点 F,延长 AF交 BC于点 G,连结 EG,CF. (1)、判断四边形AEGB 的形状,并说明理由;(2)、若 tan∠ABC= , CD=8,AD=10,求线段CF 的长.4. 如图,在中, , 分别垂直对角线于点 , .
(1)、判断四边形AEGB 的形状,并说明理由;(2)、若 tan∠ABC= , CD=8,AD=10,求线段CF 的长.4. 如图,在中, , 分别垂直对角线于点 , . (1)、求证:;(2)、若的周长为 , , 过点作于点 , , 求的长.
(1)、求证:;(2)、若的周长为 , , 过点作于点 , , 求的长.三、变式2巩固
-
5. 如图1,点P是对角线上的一点(),且使得 , 连接并延长,交于点E.
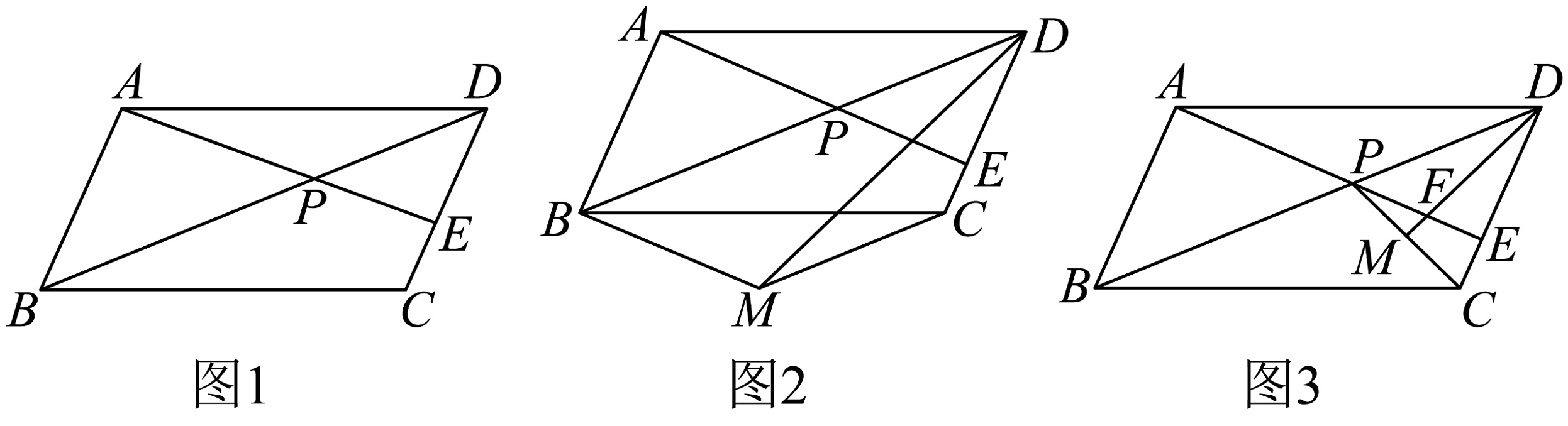 (1)、若 , 求的值.(2)、如图2,将沿方向平移到 , 求证: .(3)、如图3,连接 , 取的中点M,连接交于点F,若 , 求的值.6.
(1)、若 , 求的值.(2)、如图2,将沿方向平移到 , 求证: .(3)、如图3,连接 , 取的中点M,连接交于点F,若 , 求的值.6. (1)、【探究发现】如图①,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,M为DE 的中点,连结AM并延长交BC于点N,求证:BN=NC.(2)、【拓展应用】如图②,在四边形ABCD中,AD∥BC,对角线AC,BD交于点N,E,F分别是边AB,AD上的点,EF∥BD交AC于点M.若AD=2,BC=3,求 的值.(3)、【综合提升】如图③,在▱ABCD中,AB=4,∠ABC=60°,动点E在边AB上,过点E作EF∥BD交AC于点 F,过点F作FG⊥EF交BC于点G,连结EG.求EG的最小值.7. 如图,在每一个四边形ABCD 中,均有 AD∥BC,CD⊥BC,∠ABC=60°,AD=8,BC=12.
(1)、【探究发现】如图①,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,M为DE 的中点,连结AM并延长交BC于点N,求证:BN=NC.(2)、【拓展应用】如图②,在四边形ABCD中,AD∥BC,对角线AC,BD交于点N,E,F分别是边AB,AD上的点,EF∥BD交AC于点M.若AD=2,BC=3,求 的值.(3)、【综合提升】如图③,在▱ABCD中,AB=4,∠ABC=60°,动点E在边AB上,过点E作EF∥BD交AC于点 F,过点F作FG⊥EF交BC于点G,连结EG.求EG的最小值.7. 如图,在每一个四边形ABCD 中,均有 AD∥BC,CD⊥BC,∠ABC=60°,AD=8,BC=12. (1)、如图①,点 M 是四边形ABCD 边AD 上的一点,则△BMC的面积为.(2)、如图②,点 N 是四边形ABCD 边AD 上的任意一点,请你求出△BNC 周长的最小值.(3)、如图③,在四边形ABCD 的边AD 上,是否存在一点 P,使得cos∠BPC 的值最小? 若存在,求出此时 cos∠BPC 的值;若不存在,请说明理由.
(1)、如图①,点 M 是四边形ABCD 边AD 上的一点,则△BMC的面积为.(2)、如图②,点 N 是四边形ABCD 边AD 上的任意一点,请你求出△BNC 周长的最小值.(3)、如图③,在四边形ABCD 的边AD 上,是否存在一点 P,使得cos∠BPC 的值最小? 若存在,求出此时 cos∠BPC 的值;若不存在,请说明理由.四、变式3提高
-
8. 转化是解决数学问题常用的思想方法之一,它可以在数与数、数与形、形与形之间灵活应用.请解答下面的问题.

如图①, 在 △AOB 中, OA = OB,∠AOB=90°.
(1)、【基础巩固】将图①中△AOB绕点 B 按顺时针方向旋转60°得到△DCB,如图②,连结 OC,求证:OC=OB.
(2)、【思考探究】将图①中△AOB 绕点 B 按顺时针方向旋转60°并缩小得到△DCB,如图③,使 , 连结OC,AD.
①求证:△OBC∽△ABD;
②用等式表示 AD 与AB 之间的数量关系,并说明理由.
(3)、【拓展延伸】将图①中△AOB绕点 B 按顺时针方向旋转某个角度(小于 180°)并缩小得到△DCB,如图④,使 连 结 OC,AC,AD.当OC=OB时,求 的值.
9. 现在如果我们把平行四边形沿着它的一条对角线翻折,【发现与证明】
中, , 将沿翻折至 , 连结 .
结论1:与重叠部分的图形是等腰三角形;
结论2: .
……
(1)请利用图1证明结论1或结论2(只需证明一个结论).

【理解与应用】
在中,将沿翻折至 , 连结 .
(2)如图2,已知 , 若 , , 则______°;
【探究与拓展】
在中,将沿翻折至 , 连结 .
(3)已知 , , 翻折后四边形为时,如果平分 , 求的值;
(4)已知 , , 当是直角三角形时,则______.
10. 综合与实践
【问题情境】如图,在四边形 ABCD中,P 是线段 BC 上一点,∠APD=90°,AP=PD.
【性质初探】如图①,当∠B=∠C=90°时,猜想AB,CD,BC三条线段存在的数量关系,并证明;
【类比再探】如图②,延长 BA,CD 交于点E,当 AB⊥CD,∠B=30°时,求 的值;
【问题解决】如图②,延长 BA,CD 交于点E,当AB⊥CD,∠B=α时,用含α的代数式表示 的值.
五、原题26
-
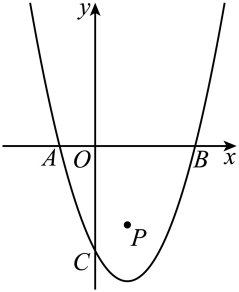
11. 如图,已知二次函数y=ax(x﹣4)(a≠0)的图象过点A(2,2),连接OA点P(x1 , y1),Q(x2 , y2),R(x3 , y3)是此二次函数图象上的三个动点,且0<x3<x1<x2<2,过点P作PB∥y轴交线段OA于点B.
 (1)、求此二次函数的表达式;(2)、如图1,点C、D在线段OA上,且直线QC、RD都平行于y轴,请你从下列两个命题中选择一个进行解答:
(1)、求此二次函数的表达式;(2)、如图1,点C、D在线段OA上,且直线QC、RD都平行于y轴,请你从下列两个命题中选择一个进行解答:①当PB>QC时,求证:x1+x2>2;
②当PB>RD时,求证:x1+x3<2;
(3)、如图,若 , 延长PB交x轴于点T , 射线QT、TR分别与y轴交于点Q1 , R1 , 连接AP , 分别在射线AT、x轴上取点M、N(点N在点T的右侧),且∠AMN=∠PAO , . 记t=R1Q1﹣ON , 试探究:当x为何值时,t有最大值?并求出t的最大值.六、变式1(基础)
-
12. 已知抛物线y=x2+bx+c的对称轴为直线x=﹣1,且经过点(-4,5).(1)、求抛物线的解析式;(2)、当﹣2<x<3时,求y的取值范围.13. 已知二次函数y=-x2+bx+c经过点A(3,0)与B(0,3).(1)、求b,c的值.(2)、求该二次函数图象的顶点坐标和对称轴。
七、变式2(巩固)
-
14. 如图,二次函数的图象与轴交于两点,与轴交于点 .
 (1)、求二次函数解析式和顶点坐标.(2)、坐标平面内存在点P,满足向左、向右或向下平移个单位后均落在二次函数图象上,求平移的距离 .(3)、在二次函数图象上取点(不与点重合),使得在之间的图象上(含两点),该二次函数最大值与最小值的和等于1,请直接写出点的坐标.15. 如图,抛物线与x轴交于A(-4,0)、B(2,0)两点,与y轴交于点C.
(1)、求二次函数解析式和顶点坐标.(2)、坐标平面内存在点P,满足向左、向右或向下平移个单位后均落在二次函数图象上,求平移的距离 .(3)、在二次函数图象上取点(不与点重合),使得在之间的图象上(含两点),该二次函数最大值与最小值的和等于1,请直接写出点的坐标.15. 如图,抛物线与x轴交于A(-4,0)、B(2,0)两点,与y轴交于点C. (1)、求抛物线的解析式及顶点坐标;(2)、如图1,连接AC,BC,若点M是第二象限内抛物线上一点,过M作轴,交AC于点N,过N作交x轴于点D,求的最大值及此时点M的坐标;(3)、如图2,在(2)的条件下,当取最大值时,将抛物线沿射线AC方向平移个单位,得到新抛物线 , 新抛物线与y轴交于点K,P为y轴右侧新抛物线上一点,过P作轴交射线MK于点Q,连接PK,当为等腰三角形时,直接写出点P的坐标.
(1)、求抛物线的解析式及顶点坐标;(2)、如图1,连接AC,BC,若点M是第二象限内抛物线上一点,过M作轴,交AC于点N,过N作交x轴于点D,求的最大值及此时点M的坐标;(3)、如图2,在(2)的条件下,当取最大值时,将抛物线沿射线AC方向平移个单位,得到新抛物线 , 新抛物线与y轴交于点K,P为y轴右侧新抛物线上一点,过P作轴交射线MK于点Q,连接PK,当为等腰三角形时,直接写出点P的坐标.八、变式3(提高)
-
16. 如图,矩形的边在坐标轴上,顶点B在第一象限,且在直线上, , 点D从点O开始沿边向点A以每秒2个单位的速度移动,与此同时,点E从点A开始沿边向点O以每秒1个单位的速度移动,轴,交于点F,连接 , 当点D到达点A时,两点同时停止移动,设移动时间为t秒.
 (1)、直接写出: ______, _______(含t的代数式表示).(2)、当点D在点E的左侧时,若的面积等于2,求t的值.(3)、在整个过程中,
(1)、直接写出: ______, _______(含t的代数式表示).(2)、当点D在点E的左侧时,若的面积等于2,求t的值.(3)、在整个过程中,①若在矩形的边上能找到点P,Q,使得以E,F,P,Q为顶点的四边形为正方形,求出所有满足条件的t的值.
②以为邻边作矩形 , 连接 , 取线段的中点Q,连接 , 求的最小值(直接写出答案).
17. 如图,在平面直角坐标系中,抛物线与轴交于点 , , 与轴交于点 , 作直线 , 点是抛物线在第四象限上一个动点点不与点 , 重合 , 连结 , , 以 , 为边作▱ , 点的横坐标为 . (1)、求抛物线对应的函数表达式;(2)、当▱有两个顶点在轴上时,则点的坐标为;(3)、当▱是菱形时,求的值.(4)、当为何值时,▱的面积有最大值?
(1)、求抛物线对应的函数表达式;(2)、当▱有两个顶点在轴上时,则点的坐标为;(3)、当▱是菱形时,求的值.(4)、当为何值时,▱的面积有最大值?
-
-