【湖南卷】备战2026年中考数学真题变式阶梯训练第23~24题-在线组卷题库

1. 为了解某校七、八年级学生在某段时间内参加公益活动次数（单位：次）的情况，从这两个年级中各随机抽取20名学生进行调查．已知这两个年级的学生人数均为200人．
对抽取的七年级学生在此段时间内参加公益活动次数的统计结果如下：
平均数
方差
6.2
1.46
同时对抽取的八年级学生的调查数据进行如下统计分析．
【收集数据】从八年级抽取的学生在此段时间内参加公益活动次数如下：
9 8 6 10 8 8 7 3 6 7
7 5 8 4 8 5 7 6 8 6
【整理数据】结果如表：
次数x分组
画记
频数
2＜x≤4
T
2
4＜x≤6
正一
6
6＜x≤8
正正
10
8＜x≤10

【分析数据】数据的平均数是6.8，方差是2.76．
【解决问题】答下列问题：

(1)、请补全频数分布表和频数分布直方图；

(2)、请估计该校八年级学生在此段时间内参加公益活动次数超过6次的人数；

(3)、请从平均数、方差两个量中任选一个，比较该校七、八年级学生在此段时间内参加公益活动次数的情况．

查看试题解析

2. 杭州宇树科技公司生产的人形机器人亮相央视2025春晚，让我们看到了一个技术深度嵌入日常生活，人机协作成为常态的未来已来.某人形机器人公司为参加人形机器人半程马拉松比赛，研发团队对H1、G1两款人形机器人的性能进行6次综合测评，测评结果绘制成如下统计图表：
型号
平均数 (分)
中位数(分)
众数(分)
方差 (分²)
H1
96
95.5
a
$\frac{8}{3}$
G1
b
96
96
5

(1)、填空： $a$ = ， $b$ =；

(2)、根据测评结果，公司决定选H1机器人参加半程马拉松比赛，请你根据相关统计量说明公司选择的理由.

查看试题解析
3. 为了提升学生身体素质，某小学开展“跳绳打卡”活动，某班级体育老师分别对甲乙两名同学进行了8次一分钟跳绳测试，测试结果数据如下表1，并根据测试数据绘制数据分析表如下表2.
表1甲乙两名同学一分钟跳绳个数统计表
甲
185
165
160
185
175
180
165
185
乙
175
180
173
172
180
180
165
175
表2测试数据分析表

平均数
中位数
众数
方差
甲
175
a
185
93.75
乙
b
175
c
23.5

(1)、根据表中的信息答下列问题：表中a=；b=；C=.

(2)、如果从甲乙中选择一位，代表班级参加学校组织的校跳绳比赛，您作为同班级的一份子，您会建议谁参赛较好，请说明理由。

查看试题解析
4. 为了解学生科学实验操作情况，随机抽取甲、乙两名同学的10次实验得分，并对他们的得分情况从以下两方面整理描述如下：
操作规范性和书写准确性的得分统计表

操作规范性
书写准确性
平均数
方差
平均数
中位数
甲
4
${s_{1}}^{2}$
1.8
a
乙
4
${s_{2}}^{2}$
b
2
②书写准确性：
书写准确性的得分统计表
实验次数
1
2
3
4
5
6
7
8
9
10
甲
1
1
2
2
2
3
1
3
2
1
乙
1
2
2
3
3
3
2
1
2
1
根据以上信息，回答下列问题：

(1)、比较甲乙两人“操作规范性”的方差大小。

(2)、综合上表的统计量，请从“操作规范性”和“书写准确性”两方面对两名同学的得分进行评价并说明理由，

查看试题解析

5. 为了了解九年级学生体育训练情况，随机抽取男生、女生各 40 名进行 1分钟跳绳测试，并对测试结果进行整理，1分钟跳绳的个数用x表示，分成了四个等级，其中A：x≥180，B：160≤x<180，C：140≤x<160，D：x<140.下面给出了部分统计信息：
信息一：女生1分钟跳绳个数扇形统计图
信息二：男生1分钟跳绳个数频数统计表
等级
A
B
C
D
频数
16
a
8
3
信息三：男生和女生1分钟跳绳个数的平均数、众数、中位数、A等级所占百分比如下表：

平均数
众数
中位数
A等级所占百分比
男生
168
187
173
40%
女生
168
188
170
30%
根据以上信息，解答下列问题：

(1)、m= ， a= ；

(2)、根据以上数据分析，你认为九年级 1分钟跳绳测试中，男生成绩更优异，还是女生成绩更优异?请说明理由(写出一条理由即可)；

(3)、在跳绳个数达到 A 等级的同学中有两名男生和一名女生跳绳的个数超过了230个，体育老师随机从这三位同学中选择两位同学做经验分享，请利用画树状图或列表的方法，求选到这名女生的概率是多少.

查看试题解析
6. 学校体育组为了解本学期九年级女生体质健康的变化情况，从九年级全体女生中随机抽取 $m$ 名女生进行体质测试，并调取这 $m$ 名女生上学期的体质测试成绩进行对比．经过对两次成绩进行整理、描述和分析，得出了下面的部分信息：
【信息1】两次测试成绩（满分为100分）的频数分布直方图如下：
（数据分组： $50 \leq x < 60$ ， $60 \leq x < 70$ ， $70 \leq x < 80$ ， $80 \leq x < 90$ ， $90 \leq x \leq 100$ ）
【信息2】抽取的 $m$ 名女生上学期测试成绩在 $80 \leq x < 90$ 的具体分数是：
80 81 83 84 84 88
【信息3】抽取的 $m$ 名女生两个学期测试成绩的平均数、中位数、众数如下表：
学期
平均数
中位数
众数
上学期
82.9
$n$
84
本学期
82.9
86
86
根据以上信息，解答下列问题：

(1)、本题中， $m$ 的值为， $n$ 的值为．

(2)、学校体育组计划根据本学期统计数据安排九年级80分以下的同学参加体质加强训练项目，若九年级共有90名女生，估计参加此项目的女生人数．

(3)、小林比较了两个学期测试成绩的平均数，发现没有区别，从而得出结论：九年级女生的体质健康没有发生变化．你是否同意他的看法？请说明理由．

查看试题解析
7. 为了激发学生对人工智能的兴趣，普及人工智能知识，某初中学校组织七、八年级学生参加入工智能科普测试，为了了解活动效果，从两个年级中各抽取10名学生的成绩进行整理分析，分成A，B，C，D四组（用x表示成绩分数)，A组：90≤x≤100，B组：80≤x<90，C组：70≤x<80，D组：x<70，下面是部分信息：
七年级10人的得分：48，57，69，72，84，84，86，91，92，96：
八年级10人的得分在B组中的分数为：84，85，85，86；
两组数据的平均数、中位数、众数如下表所示：
年级
平均数
中位数
众数
七
77.8
84
a
八
77.8
b
85
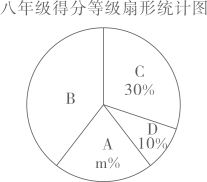
根据以上信息，解答下列问题：

(1)、填空：a= ， b= ， m=.

(2)、如果该校七年级有1000人参加测试，八年级有800人参加测试，请估计七、八两个年级得分在A组的共有多少人？

(3)、根据以上数据，你认为哪个年级在此次人工智能科普测试中表现更好，请说明理由。

查看试题解析

8. 2024年3月23日是第64个世界气象日，主题是“气候行动最前线”，学校以此为主题开展了一系列活动，在活动后期进行了气象知识竞赛，并对竞赛成绩作出如表统计分析：
【收集数据】每班随机挑选10名同学的成绩（满分10分，成绩为整数），
【描述数据】绘制成如表不完整的统计图表，
乙班成绩频数分布表
6
5
7
2
8
1
9
1
10
1
【分析数据】两个班样本数据的平均数、中位数、众数、方差如表所示，
平均数中位数众数方差
甲班 7.1 b 8 1.69
乙班 a 6.5 6 1.89
请根据所给信息，解答下列问题：

(1)、补全条形统计图；

(2)、 a= ， b=.

(3)、小明说：“这次竞赛我得了7分，在我们班中排名属中游偏上！”观察上表可知，小明是班的学生（填“甲”或“乙”）

(4)、学校准备对成绩不低于8分的同学颁发一等奖，已知甲班有48人且乙班获得一等奖的人数比甲班少64%，试估计乙班班级人数.

查看试题解析
9. 某中学科技兴趣小组为了了解本校学生对航天科技的关注程度，学校团委在八、九年级各随机抽取50名团员开展团知识竞赛，为便于统计成绩，制订了取“整十”的计分方式，满分100分．竞赛成绩如图所示．

众数
中位数
方差
八年级竞赛成绩
70
80
188
九年级竞赛成绩
m
80
n

(1)、你能用成绩的平均数判断哪个年级的成绩比较好吗？通过计算说明理由．

(2)、请根据图表中的信息，回答下列问题：
①表中m=_▲_，n=_▲_.
②现要给成绩突出的年级颁奖，如果分别从众数和方差两个角度来分析，你认为应该给哪个年级颁奖？

(3)、若规定成绩100分获特等奖，90分获一等奖，80分获二等奖，则哪个年级的获奖率高？

查看试题解析
10. 为了开展阳光体育运动，提高学生身体素质，学校开设了“引体向上”课程．为了解学生做引体向上的情况，现从八年级各班随机抽取了部分男生进行测试，绘制出不完整的统计图1和图2，请根据有关信息，解答下列问题：
（1）本次接受随机抽样调查的男生人数为　　，图1中m的值是　　；
（2）本次调查获取的样本数据（6，7，8，9，10）中，众数为　　，中位数为　　；
（3）补全条形统计图；
（4）根据样本数据，若八年级有280名男生，请你估计该校八年级男生“引体向上”次数在8次及以上的人数．

查看试题解析

11. 如图，某处有一个晾衣装置，固定立柱AB和CD分别垂直地面水平线l于点B ， D ， AB＝19分米，CD＞AB ．在点A ， C之间的晾衣绳上有固定挂钩E ， AE＝13分米，一件连衣裙MN挂在点E处（点M与点E重合），且直线MN⊥l ．

(1)、如图1，当该连衣裙下端点N刚好接触到地面水平线l时，点E到直线AB的距离EG等于12分米，求该连衣裙MN的长度；

(2)、如图2，未避免该连衣裙接触到地面，在另一端固定挂钩F处再挂一条长裤（点F在点E的右侧），若∠BAE＝76.1°，求此时该连衣裙下端N点到地面水平线l的距离约为多少分米？
（结果保留整数，参考数据：sin76.1°≈0.97，cos76.1°≈0.24，tan76.1°≈4.04）

查看试题解析

12. 数学兴趣小组测量学校旗杆的高度，经历了以下操作（如示意图所示）：①先将旗杆上绳子AC向外拉紧；②测量出在点 C处观察旗杆顶端A的仰角α=83°；③测量出点 C到旗杆的距离=1 m；④测量出点 C到地面的距离y=1.5m.求旗杆 AB 的高为多少m.（参考数据：sin 83°≈0.993，cos 83°≈0.122，tan 83°≈8.144，结果保留两位小数

查看试题解析
13. 某停车场入口的栏杆如图所示，栏杆从水平位置AB绕点 $O$ 旋转到CD的位置．已知 $A O = 4$ 米，若栏杆的旋转角 $∠ A O D = 2 8^{°}$ ，求栏杆端点 $A$ 升高的高度约为多少米？（精确到0.01）

（参考数据如下，sin28°≈0.469，cos28°≈0.883，tan28°≈0.532）

查看试题解析
14. 小区内开车必须遵守限速 $5 m / s$ 安全规范．如图，在某小区拐角处的一段道路上，有一儿童在 $C$ 处玩要，一辆汽车从被楼房遮挡的拐角另一侧的 $A$ 处驶来，经过2秒直行到 $B$ 处刚好观察到 $C$ 处的儿童（此时B，O，C三点共线）．已知 $C M = 3 m, O C = 5 m, O D = 3 m, ∠ O A D = 2 0^{°}$ ，试问该汽车是否遵守行车安全规范？
（参考数据： $c o s 2 0^{°} \approx 0.94, s i n 2 0^{°} \approx 0.34, t a n 2 0^{°} \approx 0.36$ ）

查看试题解析

15. 问题情境：筒车是我国古代发明的一种水利灌溉工具，既经济又环保.明代科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(如图①).假定在水流量稳定的情况下，筒车上的每一个盛水筒都沿逆时针方向做匀速圆周运动，每旋转一周用时 120秒.
问题设置：把筒车抽象为一个半径为2米的⊙O，如图②.OM始终垂直于水平面，在某一时刻，某盛水筒恰好位于水面A处，此时∠AOM=30°，经过95秒后该盛水筒运动到点B处.
问题解决：

(1)、求∠BOM的度数；

(2)、求该盛水筒旋转至B处时，它到水面的距离.(结果精确到0.1米，参考数据： $\sqrt{2} \approx 1.414, \sqrt{3} \approx 1.732)$

查看试题解析
16. 如图1是某路政部门正在维修路灯的实物图片，可抽象为如图2所示模型，路灯AB和汽车折臂升降机的折臂底座CD都垂直于地面MN，且它们之间的水平距离BC=3m，折臂底座高CD=1.5m，上折臂AE与下折臂DE的夹角∠AED=87°，下折臂DE与折臂底座的夹角∠CDE=135°，下折臂端点E到地面MN距离是4.5m.（结果精确到0.1m，参考数据：sin42°≈0.67，cos42°≈0.74， tan42°≈0.90， $\sqrt{2}$ ≈1.41)

(1)、求下折臂 DE 的长；

(2)、求路灯 AB 的高.

查看试题解析
17. 综合实践：如何测量出路灯的灯杆和灯管支架的长度?
素材1：如图①，一种路灯由灯杆AB和灯管支架 BC两部分构成，已知灯杆AB与地面垂直，灯管支架 BC 与灯杆AB 的夹角∠ABC=127°.
素材2：如图②，在路灯正前方的点 D 处测得∠ADB=37°，∠ADC=45°，AD=400 cm.
根据以上素材解决问题：
(结果精确到 1 cm.参考数据： sin 37°≈0.60， cos 37°≈0.80， tan 37°≈0.75)

(1)、求灯杆 AB 的长度；

(2)、求灯管支架 BC的长度.

查看试题解析

18. 随着电动汽车和AI技术的不断发展，通过传感器、人工智能算法、控制器等技术，实现车辆的自主驾驶功能．在检测到障碍物场景下，智能汽车自动通过智算达到自动刹车（或绕过障碍物）．整个刹车过程反应时间分：1、感知障碍物并传输信息；2、计算决策；3、执行决策（刹车或绕行）．从感知到开始执行刹车前，智能系统总反应时间 $0.1 - 0.6$ 秒之间，低于人类驾驶员 $0.8 - 2$ 秒的反应时间．
总停车距离（ $l$ ） = 反应距离（ $t v$ ） + 制动距离（ $\frac{v^{2}}{2 a}$ ）：记作为： $l = t v + \frac{v^{2}}{2 a}$ （ $l$ ：从感知到车停共经过的距离，单位米； $t$ ：感知、计算的反应时间，单位秒； $v$ ：刹车前行车速度，单位米/秒； $a$ ：减速度，单位米/秒）．经实地测试，智能汽车在不同行驶速度下检测到障碍物时，刹车制动距离的数据如下：
车速 $x$ （千米/时）
72
108
┄
停车距离 $l$ （米）
35
71.25
┄

(1)、请根据素材求：从感知到车停共经过的距离 $l$ 与刹车前行车速度 $v$ 的函数表达式；

(2)、请根据素材回答问题：某智能测试汽车以 $64.8$ 千米/时正在一个车道正中间行驶时，某时刻前方相距 $s = 27$ 米的货车上突然掉下一包货物几乎布满整个车道（假设掉地后静止不动）．测试汽车感知后立即启动智能程序并计算，
①请你判断，智能汽车不改变方向情况下，能否在货物前停车？
②当汽车在高速行驶时（ $v \geq 60$ 千米/时），汽车紧急拐弯的角度可以达到 $5.7 °$ ，在不减速的情况下拐弯绕行避险，能否成功？
（参考数据：每个车道的宽度为 $d = 3.75$ 米 $sin 5.7 ° = 0.099 ， cos 5.7 ° = 0.995 ， tan 5.7 ° = 0.1$ ）

查看试题解析
19. 足球射门时，在不考虑其他因素的条件下，射点到球门AB的张角越大，射门越好.当张角达到最大值时，我们称该射点为最佳射门点.通过研究发现，如图1所示，运动员带球在直线CD上行进时，当存在一点Q，使得 $∠ C Q A = ∠ A B Q$ （此时也有 $∠ D Q B = ∠ Q A B$ ）时，恰好能使球门AB的张角 $∠ A Q B$ 达到最大值，故可以称点Q为直线CD上的最佳射门点.

(1)、如图2所示，AB为球门，当运动员带球沿CD行进时， $Q_{1}$ ， $Q_{2}$ ， $Q_{3}$ 为其中的三个射门点，则在这三个射门点中，最佳射门点为点；

(2)、如图3所示，是一个矩形形状的足球场，AB为球门， $C D ⊥ A B$ 于点D， $A B = 3 a$ ， $B D = a$ .某球员沿CD向球门AB进攻，设最佳射门点为点Q.
①用含a的代数式表示DQ的长度并求出 $t a n ∠ A Q B$ 的值；

②已知对方守门员伸开双臂后，可成功防守的范围为 $\frac{\sqrt{5}}{4} a$ ，若此时守门员站在张角 $∠ A Q B$ 内，双臂张开MN垂直于AQ进行防守，求MN中点与AB的距离至少为多少时才能确保防守成功.（结果用含a的代数式表示）

查看试题解析
20. 汽车盲区是指驾驶员位于驾驶座位置，其视线被车体遮挡而不能直接观察到的区域．如图， $△ A B C$ 、 $△ F E D$ 分别为汽车两侧盲区的示意图，已知视线 $P B$ 与地面 $B E$ 的夹角 $∠ P B E = 43^{\circ}$ ，视线 $P E$ 与地面 $B E$ 的夹角 $∠ P E B = 20^{\circ}$ ，点 $A$ ， $F$ 分别为 $P B$ ， $P E$ 与车窗底部的交点， $A F ∥ B E$ ， $A C$ ， $F D$ 垂直地面 $B E$ ， $A$ 点到 $B$ 点的距离 $A B = 1.6 m$ ．（参考数据： $sin 43^{\circ} \approx 0.7$ ， $tan 43^{\circ} \approx 0.9$ ， $sin 20^{\circ} \approx 0.3$ ， $tan 20^{\circ} \approx 0.4$

(1)、求车窗底部到地面的高度（即 $A C$ 的长）；

(2)、求盲区中 $D E$ 的长度；

(3)、点 $M$ 在 $E D$ 上， $M D = 1.8 m$ ，在 $M$ 处有一个高度为 $0.5 m$ 的物体，驾驶员能观察到物体吗？请说明理由．

查看试题解析

【湖南卷】备战2026年中考数学真题变式阶梯训练第23~24题

一、原题23

二、变式1基础

三、变式2巩固

四、变式3提高

五、原题24

六、变式1（基础）

七、变式2（巩固）

八、变式3（提高）

次数x分组	画记	频数
2＜x≤4	T	2
4＜x≤6	正一	6
6＜x≤8	正正	10
8＜x≤10

型号	平均数 (分)	中位数(分)	众数(分)	方差 (分²)
H1	96	95.5	a	$\frac{8}{3}$
G1	b	96	96	5

	操作规范性		书写准确性
	平均数	方差	平均数	中位数
甲	4	${s_{1}}^{2}$	1.8	a
乙	4	${s_{2}}^{2}$	b	2

	平均数	众数	中位数	A等级所占百分比
男生	168	187	173	40%
女生	168	188	170	30%

学期	平均数	中位数	众数
上学期	82.9	$n$	84
本学期	82.9	86	86

车速 $x$ （千米/时）	72	108	┄
停车距离 $l$ （米）	35	71.25	┄

平均数	方差
6.2	1.46

甲	185	165	160	185	175	180	165	185
乙	175	180	173	172	180	180	165	175

等级	A	B	C	D
频数	16	a	8	3

年级	平均数	中位数	众数
七	77.8	84	a
八	77.8	b	85