（期中真题汇编）人教版七（上）期中复习专题六整式加减

试卷更新日期：2025-10-20 类型：复习试卷

进入出卷网下载

一、选择题

1. 在式子 $2 x + 3 y$ ， $\frac{2}{a}$ ， $0.5$ ， $\frac{b + 2}{2}$ ， $- 2 x$ ， $3 a^{2} b$ ， $\frac{a}{π}$ 中，单项式的个数是（）

A、 $2$ 个 B、 $3$ 个 C、 $4$ 个 D、 $5$ 个

查看试题解析
2. 下列各组中的两项是同类项的是（）

A、 $6 z y^{2}$ 和 $- 2 y^{2} z$ B、 $- m^{2} n$ 和 $m n^{2}$ C、 $- x^{2}$ 和 $3 x$ D、 $0.5 a$ 和 $0.5 b$

查看试题解析
3. 单项式 $- \frac{π x^{2} y}{3}$ 的系数是（）

A、 $\frac{π}{3}$ B、 $- \frac{1}{3}$ C、 $\frac{1}{3}$ D、 $- \frac{π}{3}$

查看试题解析
4. 下列说法正确的是（　　）

A、 $\frac{1}{2} a^{2} b$ 是二次单项式 B、 $a^{3} + a^{2}$ 是五次二项式 C、 $a^{2} + a - 1$ 的常数项是1 D、 $- \frac{a^{3} b^{2} c}{5}$ 的系数是 $- \frac{1}{5}$

查看试题解析
5. 下列计算正确的是（）

A、 $m^{2} + m^{2} = m^{4}$ B、 $5 a^{2} - 4 a^{2} = 1$ C、 $3 a + 2 b = 5 a b$ D、 $3 a^{2} b - 3 b a^{2} = 0$

查看试题解析
6. 下列计算正确的是（）

A、 $5 a + 6 b = 11 a b$ B、 $9 a - a = 9$ C、 $a + 3 a = 4 a^{2}$ D、 $3 a b + 4 b a = 7 a b$

查看试题解析
7. 如图，将一个长方形ABCD分成4个长方形，其中②与③的大小形状相同，已知大长方形ABCD的边 $B C = 5.5$ ，则①与④两个小长方形的周长和为（）

A、22.5 B、22 C、21.5 D、20

查看试题解析
8. 图1是长为 $a$ ，宽为 $b (a > b)$ 的小长方形纸片将6张如图1的纸片按图2的方式不重叠地放在长方形 $A B C D$ 内，已知 $C D$ 的长度固定不变， $B C$ 的长度可以变化，图中阴影部分（即两个长方形）的面积分别表示为 $S_{1}$ ， $S_{2}$ ，若 $S = S_{1} - S_{2}$ ，且 $S$ 为定值，则 $a$ ， $b$ 满足的关系是（）

A、 $a = 2 b$ B、 $a = 3 b$ C、 $a = 4 b$ D、 $a = 5 b$

查看试题解析
9. 三张大小不一的正方形纸片按如图1和图2方式分别放置于相同的长方形中，它们既不重叠也无空隙，记图1阴影部分周长之和为m，图2阴影部分周长为n，要求m与n的差，只需知道一个图形的边长，这个图形是（）

A、整个长方形 B、图①正方形 C、图②正方形 D、图③正方形

查看试题解析
10. 在长方形ABCD内，将两张边长分别为a和 $b (a > b)$ 的正方形纸片按图①，②两种方式放置（图①，②中两张正方形纸片均有部分重叠），长方形中未被这两张正方形纸片覆盖的部分用阴影表示.若 $A D = m ， A B = n$ ，图①中阴影部分的面积表示为 $S_{1}$ ，图②中阴影部分的面积表示为 $S_{2}$ ， $S_{2} - S_{1}$ 的值与a，b，m，n四个字母中哪个字母的取值无关（）

A、与a的取值无关 B、与b的取值无关 C、与m的取值无关 D、与n的取值无关.

查看试题解析
11. 已知 $M = 4 x^{2} - 3 x - 2 ， N = 6 x^{2} - 3 x + 6$ ，则 $M$ 与 $N$ 的大小关系是（）

A、 $M < N$ B、 $M > N$ C、 $M = N$ D、以上都有可能

查看试题解析
12. 要使多项式 $m x^{2} - (5 - x + x^{2})$ 化简后不含x的二次项，则m等于（）

A、0 B、1 C、 $- 1$ D、 $- 5$

查看试题解析

二、填空题

13. 请你写出一个单项式，使它的系数为负数，次数为3：．

查看试题解析
14. $- \frac{π}{4} b^{2}$ 的系数是．

查看试题解析
15. 若 $- x^{2 m + 1} y^{5}$ 与 $\frac{3}{5} x^{9} y^{3 t + 8}$ 是同类项，则 $m - t =$ ．

查看试题解析
16. 多项式 $2 a^{3} b^{2} - 5 a b^{3} - a b^{2} - 7 a b + 3$ 的三次项系数是．

查看试题解析
17. 已知多项式 $5 x^{2} - m x + 1 + 3 m$ 的值与m的大小无关，则该多项式的值为

查看试题解析
18. 多项式 $3 m x^{2} - n y + 3 y - 5 + 6 x^{2}$ 的值与x，y的取值无关，则 ${(m + n)}^{2025}$ 的值为．

查看试题解析
19. 如果代数式 $4 x^{4} + 5 x^{3} + 2 m x^{2} - n x^{3} + 6 x^{2} + 9$ 中不含 $x^{2}$ 和 $x^{3}$ 项，则 $m n =$ ．

查看试题解析
20. 一个多项式加上 $- x^{2} + x - 2$ 得 $x^{2} - 1$ ，则此多项式应为.

查看试题解析
21. 在计算两位数的平方运算时，我们可以利用“竖式”方式进行快速运算，其步骤如图所示（图1，2，3），现有一个两位数，其十位数字为 $x$ ，在进行平方运算时，部分步骤如图4所示（ $x$ 为小于 $5$ 的正整数），则这个两位数是（用含 $x$ 的代数式表达）．

查看试题解析

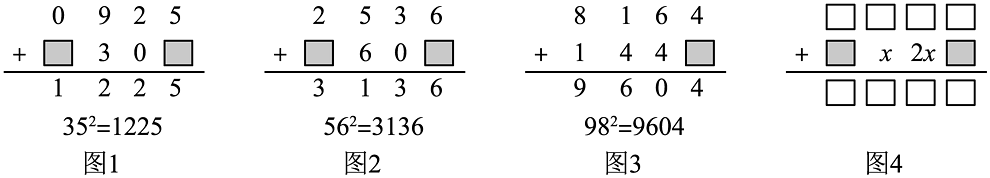
三、解答题

22. 已知 $A = 2 a^{2} + 3 a b - 2 a - 1 ， B = a^{2} - \frac{1}{2} a b - \frac{2}{3}$ ．

(1)、当 $a = - 1 ， b = - 2$ 时，求 $A - 2 B$ 的值；

(2)、若 $A - 2 B$ 的值与 $a$ 的取值无关，求 $b$ 的值．

查看试题解析
23. 已知： $A = x^{2} + 2 x - 1, B = 3 x^{2} - 2 a x + 1$ ．

(1)、当 $x = 1, a = - 3$ 时，求 $B$ 的值；

(2)、用含 $a, x$ 的代数式表示 $3 A - B$ ；

(3)、若 $3 A - B$ 的值与 $x$ 无关，求 $a$ 的值．

查看试题解析
24. 设 $A = - 3 b^{2} + 4 a b + 2 c, B = - 2 b^{2} + 2 a b + 2 c$ ．

(1)、求 $2 A - 3 B$ ．

(2)、当b为 $1, 2, 4$ 时，代数式 $2 A - 3 B$ 的值分别是 $m, 3, n$ ，求 $2 m + n$ 的值．

查看试题解析
25. 已知 $A = a^{2} - 2 a b + b^{2}, B = a^{2} + 2 a b + b^{2}$ ．

(1)、求 $A + B$ ；

(2)、求 $\frac{1}{2} (B - A)$ ；

(3)、如果 $3 A - 2 B + C = 0$ ，那么C的表达式是什么？

查看试题解析
26. 今年暑假小明家买了一套经济适用房，他准备将地面铺上地砖，这套住宅的建筑平面图（由四个长方形组成）如图所示（图中长度单位：米）．

(1)、求出用含 $x$ 、 $y$ 的代数式表示这套房的总面积是多少平方米?

(2)、当 $x = 3$ ， $y = 1.5$ 时，若铺1平方米地砖平均费用120元，求这套住宅铺地砖总费用．

查看试题解析
27. 如图，有三张正方形纸片A，B，C，它们的边长分别为a，b，c，将三张纸片按图1，图2两种不同方式放置于同一长方形中，记图1中阴影部分周长为l₁ ，图2中阴影部分周长为l₂ ．

(1)、若 $a = 7, b = 5, c = 3$ ，则长方形的周长为　　；

(2)、若 $b = 7, c = 4$
①求 $l_{1} - l_{2}$ 的值；
②记图1中阴影部分面积为 $S_{1}$ ，图2中阴影部分面积为 $S_{2}$ ，求 $S_{2} - S_{1}$ 的值．

查看试题解析
28. 如图，正方形 $A B C D$ 的边长为8，划分成 $8 \times 8$ 个小正方形格．将边长为 $n$ （ $n$ 为整数，且 $2 \leq n \leq 7$ ）的黑灰两色正方形纸片按图中的方式黑灰相间地摆放，第一张 $n \times n$ 的纸片正好盖住正方形 $A B C D$ 左上角的 $n \times n$ 个小正方形格，第二张纸片盖住第一张纸片的部分恰好为 $(n - 1) \times (n - 1)$ 的正方形．如此摆放下去，最后直到纸片盖住正方形 $A B C D$ 的右下角为止．
请你认真观察思考后回答下列问题：

(1)、由于正方形纸片边长 $n$ 的取值不同，完成摆放时所使用正方形纸片的张数也不同，请填写下表：
纸片的边长 $n$
2
3
4
使用的纸片张数
7
_____
_____

(2)、设正方形 $A B C D$ 被纸片盖住的面积（重合部分只计一次）为 $S_{1}$ ，未被盖住的面积为 $S_{2}$ ．
①当 $n = 2$ 时，求 $S_{1} : S_{2}$ 的值；
②用含 $n$ 的代数式表示 $S_{2}$ （用含 $n$ 的代数式表示，不用化简）．

查看试题解析
29. 如图，四边形 $A B C D$ 和四边形 $C E F G$ 都是正方形．

(1)、用代数式表示阴影部分的面积；（结果要求化简）

(2)、当 $a = 4$ 时，求阴影部分的面积．

查看试题解析
30. 我市某小区居民使用自来水2023年标准缴费如下（水费按月缴纳）：
用户月用水量
单价
不超过 $12 m^{3}$ 的部分
$a$ 元 $/ m^{3}$
超过 $12 m^{3}$ 但不超过 $20 m^{3}$ 的部分
$1.5 a$ 元 $/ m^{3}$
超过 $20 m^{3}$ 的部分
$2 a$ 元 $/ m^{3}$

(1)、当 $a = 2$ 时，
①某户1月份用了 $3 m^{3}$ 的水，求该户1月份应缴纳的水费__________元．
②某户4月份用了 $13 m^{3}$ 的水，求该户4月份应缴纳的水费__________元．
③某户8月份用了 $23 m^{3}$ 的水，求该户8月份应缴纳的水费__________元．

(2)、设某户月用水量为 $n m^{3}$ ，当 $n > 20$ 时，该户应缴纳的水费为__________元（用含 $a$ ， $n$ 的式子表示）．

(3)、当 $a = 2$ 时，甲、乙两户一个月共用水 $40 m^{3}$ ，已知甲户缴纳的水费超过了24元，设甲户这个月用水 $x m^{3}$ ，试求甲，乙两户一个月共缴纳的水费（用含 $x$ 的式子表示）

查看试题解析

用户月用水量	单价
不超过 $12 m^{3}$ 的部分	$a$ 元 $/ m^{3}$
超过 $12 m^{3}$ 但不超过 $20 m^{3}$ 的部分	$1.5 a$ 元 $/ m^{3}$
超过 $20 m^{3}$ 的部分	$2 a$ 元 $/ m^{3}$

纸片的边长 $n$	2	3	4
使用的纸片张数	7	_____	_____

（期中真题汇编） 人教版七（上） 期中复习 专题六 整式加减

一、选择题

二、填空题

三、解答题

（期中真题汇编）人教版七（上）期中复习专题六整式加减