【湖南卷】备战2026年中考数学真题变式阶梯训练第15~16题-在线组卷题库

1. 甲、乙两人在一次100米赛跑比赛中，路程s（米）与时间t（秒）的函数关系如图所示，填（“甲”或“乙”先到终点）．

查看试题解析

2. 甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.图中l_甲， l_乙分别表示甲、乙两人前往目的地所行驶的路程s(千米)随时间t(分)变化的函数图象，则每分钟乙比甲多行驶千米.

查看试题解析
3. A ， B两地相距 $100 k m$ ，甲、乙两人骑车同时分别从A ， B两地相向而行．假设他们都保持匀速行驶，甲、乙两人各自到A地的距离 $s (k m)$ 与骑车时间 $t (h)$ 的关系如图所示，则他们相遇时距离A地 $k m$ ．

查看试题解析
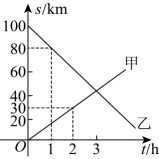4. 甲、乙两人在一次赛跑中，路程 $s$ （米）与时间 $t$ （秒）的关系如图所示．当第一个人到达终点时，第二个人距离终点还剩米．

查看试题解析

5. 某公司准备与汽车租赁公司签订租车合同，以每月用车路程x（千米）计算，甲汽车租赁公司每月收取的租赁费为y₁元，乙汽车租赁公司每月收取的租赁费为y₂元，y₁ ， y₂与x之间的函数关系如图所示.当月用车路程为2300千米时，选汽车租赁公司比较合算.

查看试题解析
6. 周末，骑行爱好者甲、乙两人相约沿同一路线从 $A$ 地出发前往 $B$ 地进行骑行训练，甲、乙分别以不同的速度匀速骑行，乙比甲早出发5分钟．乙骑行25分钟后，甲以原速的 $\frac{8}{5}$ 继续骑行，经过一段时间，甲先到达 $B$ 地，乙一直保持原速前往 $B$ 地．在此过程中，甲、乙两人相距的路程 $y$ (米)与乙骑行的时间 $x$ (分钟)之间的关系如图所示，则乙比甲晚分钟到达 $B$ 地．

查看试题解析
7. $A ， B$ 两地相距的路程为240千米，甲、乙两车沿同一线路从 $A$ 地出发到 $B$ 地，分别以一定的速度匀速行驶，甲车先出发40分钟后，乙车才出发.途中乙车发生故障，修车耗时20分钟，随后，乙车车速比发生故障前减少了10千米/小时（仍保持匀速前行），甲、乙两车同时到达 $B$ 地.甲、乙两车相距的路程 $y$ （千米）与甲车行驶时间 $x$ （小时）之间的关系如图所示，求乙车修好时，甲车距 $B$ 地还有千米.

查看试题解析

8. 甲地宏达物流公司的快递车和货车同时从甲地出发，以各自的速度沿快速通道向乙地匀速行驶，快递车到达乙地后，卸完物资并另装货物共用了 45 分钟，然后按原路以另一速度返回，直至与货车相遇．已知货车行驶速度为 60 km/h，两车间的距离 y(km) 与货车行驶时间 x(h) 之间的函数图象如图所示：
给出以下四个结论：
① 快递车从甲地到乙地的速度是 100 km/h；
② 甲、乙两地之间的距离是 80 km；
③ 图中点 B 的坐标为 ( $2 \frac{3}{4}$ ， 35)；
④ 快递车从乙地返回时的速度为 90 km/h．
其中正确的是（填序号）．

查看试题解析
9. 沿河岸有A，B，C三个港口，甲乙两船同时分别从AB港口出发，匀速驶向C港，最终到达C港．设甲、乙两船行驶x（h）后，与B港的距离分别为y₁、y₂（km），y₁、y₂与x的函数关系如图所示．考察下列结论：
①乙船的速度是25km/h；②从A港到C港全程为120km；③甲船比乙船早1.5小时到达终点；④若设图中两者相遇的交点为P点，P点的坐标为（ $\frac{7}{6}$ ， $\frac{100}{3}$ ）；⑤如果两船相距小于10km能够相互望见，那么甲、乙两船可以相互望见时，x的取值范围是 $\frac{2}{3}$ ＜x＜2．其中正确的结论有．

查看试题解析
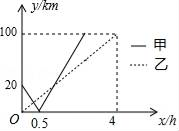10. 在全民健身环城越野赛中，甲、乙两选手的行程y(千米)随时间x(时)变化的图象(全程)如图所示.有下列说法：①起跑后1小时内，甲在乙的前面；②第1小时两人都跑了10千米；③甲比乙先到达终点；④两人都跑了20千米.其中说法正确的序号是.

查看试题解析

11. 如图，在△ABC中，BC＝6，点E是AC的中点，分别以点A ， B为圆心，以大于 $\frac{1}{2} A B$ 的长为半径画弧，两弧相交于点M ， N ，直线MN交AB于点D ，连接DE ，则DE的长是．

查看试题解析

12. 如图，在 $△ A B C$ 中， $A B = A C$ ，分别以点A和点B为圆心，大于 $\frac{1}{2} A B$ 的长为半径作弧，两弧相交于M，N两点，作直线 $M N$ 交 $B C$ 于点D，连接 $A D$ ，若 $∠ B = 50 °$ ，则 $∠ D A C =$ ．

查看试题解析
13. 如图， $a ∥ b$ ，直线 $l$ 与直线 $a ， b$ 分别交于 $B ， A$ 两点，分别以点 $A ， B$ 为圆心，大于 $\frac{1}{2} A B$ 的长为半径画弧，两弧相交于点 $E ， F$ ，作直线 $E F$ ，分别交直线 $a ， b$ 于点 $C ， D$ ，连结 $A C$ ，若 $∠ C D A = 34^{\circ}$ ，则 $∠ C A B$ 的度数为.

查看试题解析
14. 如图，已知线段 $A B$ ，分别以点 $A ， B$ 为圆心，线段 $A B$ 的长为半径画弧，两弧相交于点 $C ， D$ ，连结 $A C ， B C ， B D ， C D ， A D$ ．则 $∠ A C D$ 为度．

查看试题解析

15. 如图，在 $△ A B C$ 中，以点 $A$ 为圆心， $A C$ 长为半径作弧，交 $B C$ 于 $C ， D$ 两点，分别以点 $C$ 和点 $D$ 为圆心，大于 $\frac{1}{2} C D$ 长为半径作弧，两弧交于点 $P$ ，作直线 $A P$ ，交 $C D$ 于点 $E$ ．若 $A C = 5 ， C D = 6$ ，则 $A E =$

查看试题解析
16. 如图， $▱ A B C D$ 中， $B D$ 为对角线，分别以点A、B为圆心，以大于 $\frac{1}{2} A B$ 的长为半径画弧，两弧相交于点M、N，作直线 $M N$ 交 $A D$ 于点E，交 $A B$ 于点F，若 $A D ⊥ B D$ ， $B D = 4$ ， $B C = 8$ ，则 $A E$ 的长为．

查看试题解析
17. 如图，在Rt $△ A B C$ 中， $∠ A C B = 90^{\circ} ， A C = 2 B C$ ，分别以点 $A$ 和 $B$ 为圆心，以大于 $\frac{1}{2} A B$ 的长为半径作弧，两弧相交于点 $M$ 和 $N$ ，作直线 $M N$ ，交 $A C$ 于点 $E$ ，连结 $B E$ ，若 $C E = 3$ ，则 $B E$ 的长为.

查看试题解析

18. 如图，在矩形ABCD中， $A B = 4$ ， $B C = 8$ ， E，F分别为AB，BC的中点，连结CE，DF，取CE，DF的中点M，N，连结MN，则MN的长为.

查看试题解析
19. 如图，在矩形 ABCD 中，对角线 AC，BD 交于点 O， $∠ B A C$ 的平分线交 BC 于点 E，连结 OE.已知 $O E = \sqrt{10}$ ， $∠ A E O = 4 5^{°}$ ，则 AB=.

查看试题解析
20. 如图，在正方形 ABCD 中，E，F 分别是边 AB，BC的中点，连结EC，FD，G，H 分别是 EC，FD 的中点，连结GH.若AB=4，则GH的长度为.

查看试题解析

【湖南卷】备战2026年中考数学真题变式阶梯训练第15~16题

一、原题15

二、变式1基础

三、变式2巩固

四、变式3提高

五、原题16

六、变式1（基础）

七、变式2（巩固）

八、变式3（提高）