《圆》精选压轴题（一）—2025年浙江省九（上）数学期中复习

试卷更新日期：2025-10-19 类型：复习试卷

进入出卷网下载

一、单选题

1. 如图，在以点O为圆心的半圆中，AB是直径， $\overset{⌢}{A D}$ ＋ $\overset{⌢}{B C}$ ＝ $\overset{⌢}{C D}$ ，连接AC，BD交于点E，连接OC交BD于点F，若CE＝ $\frac{1}{2}$ AB，则CE：CA的值是（）

A、 $\frac{2}{3}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{3}{4}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
2. 如图，平面直角坐标系中， $⊙ P$ 经过三点 $A (8 ， 0) ， O (0 ， 0) ， B (0 ， 6)$ ，点D 是 $⊙ P$ 上的一动点．当点 D 到弦 $O B$ 的距离最大时，点D 的坐标是（）

A、 $(9 ， 3)$ B、 $(9 ， 6)$ C、 $(10 ， 3)$ D、 $(10 ， 6)$

查看试题解析
3. 如图，已知△ABC，O为AC上一点，以OB为半径的圆经过点A，且与BC，OC交于点D，E．设∠A=α，∠C=β（　　）

A、若α+β=70°，则 $\overset{⌢}{D E}$ 的度数为20° B、若α+β=70°，则 $\overset{⌢}{D E}$ 的度数为40° C、若α﹣β=70°，则 $\overset{⌢}{D E}$ 的度数为20° D、若α﹣β=70°，则 $\overset{⌢}{D E}$ 的度数为40°

查看试题解析
4. 已知⊙O为ΔABC的外接圆，AB=BC.过A作CO的垂线交CO延长线于点D，则下列选项一定成立的是（）

A、 $∠ B C A = ∠ D C A$ B、 $∠ D A C = 2 ∠ B A C$ C、 $A B > 2 A D$ D、 $4 A B^{2} < A D^{2} + C D^{2}$

查看试题解析
5. 如图，以第三象限内一点 $P$ 为眐心，大于PO的长为半径作 $⊙ P$ ，分别交x轴于点A，B，交y轴于点 $C, D$ ，记该圆面在第一，二，三，四象限内各部分的面积分别为 $S_{1} ， S_{2} ， S_{3}, S_{4}$ ，若 $| S_{1} + S_{3} - S_{2} - S_{1} |$ 是一个定值，则（）

A、 $⊙ P$ 的半径是一个定值 B、 $| P F^{2} - P E^{2} |$ 是一个定值 C、点 $P$ 是一个定点 D、点 $P$ 在一个确定的函数图象上

查看试题解析
6. 如图，已知 $⊙ O$ 中，直径 $A F ⊥ B C$ 于点H，点D在 $A B$ 上，且 $∠ A C D = 30 °$ ，过点A作 $A E ⊥ C D$ 于点E，已知 $△ B C D$ 的周长为 $6 \sqrt{3} + 4$ ，且 $B H = 2$ ，则 $⊙ O$ 的半径长为（）

A、 $3 \sqrt{3}$ B、 $\frac{7 \sqrt{3}}{2}$ C、 $\frac{5 \sqrt{2}}{2}$ D、 $\frac{9 \sqrt{2}}{4}$

查看试题解析
7. 已知 $⊙ O$ 为 $△ A B C$ 的外接圆， $A B = B C$ ．过 $A$ 作 $C O$ 的垂线交 $C O$ 延长线于点 $D$ ，则下列选项一定成立的是（）

A、 $∠ B C A = ∠ D C A$ B、 $∠ D A C = 2 ∠ B A C$ C、 $A B > 2 A D$ D、 $4 A B^{2} < A D^{2} + C D^{2}$

查看试题解析
8. 如图，点A，B，C，D在 $⊙ O$ 上，连接 $A B$ ， $B C$ ， $C D$ ．若 $A B = 8$ ， $C D = 5$ ， $∠ B + ∠ C = 60 °$ ，则 $⊙ O$ 的半径为（）

A、 $\frac{9}{2}$ B、 $\frac{7 \sqrt{3}}{3}$ C、 $3 \sqrt{3}$ D、5

查看试题解析
9. 如图，等腰 $Rt △ A B C$ 内接于圆O，直径 $A B = 2 \sqrt{2}$ ， D是圆上一动点，连接 $A D ， C D$ ， $B D$ ，且 $C D$ 交 $A B$ 于点G．下列结论：① $D C$ 平分 $∠ A D B$ ；② $∠ D A C = ∠ A G C$ ；③当 $A D = C D$ ，四边形 $A D B C$ 的面积为 $8 \sqrt{3}$ ；④当 $B D = 2$ 时，四边形 $A D B C$ 的周长最大，正确的有（）

A、①② B、②③ C、①②④ D、①③④

查看试题解析

二、填空题

10. 如图， $A B$ 是 $⊙ O$ 一条弦，将劣弧沿弦 $A B$ 翻折，连结 $A O$ 并延长交翻折后的弧于点 $C$ ，连结 $B C$ ．若 $⊙ O$ 的半径长为 $2$ ， $B C = 1$ ，则 $A B =$ ．

查看试题解析
11. 如图， A B 为 $⊙ O$ 的直径，且 $A B = 26$ ，点 $C$ 为 $⊙ O$ 上半圆的一点， $C E ⊥ A B$ 于点 $E$ ， $∠ O C E$ 的角平分线交 $⊙ O$ 于点 $D$ ，弦 $A C = 10$ ，那么 $△ A C D$ 的面积是.

查看试题解析
12. 如图，有两个半径分别为 $\sqrt{5}$ 和 $2 \sqrt{5}$ 的同心圆，矩形ABCD的边AB，CD分别为两圆的弦，那么矩形ABCD面积的最大值时AB的长为.

查看试题解析
13. 我国古代数学家刘徽利用圆内接正多边形创立了“割圆术”，现将半径为2的圆十二等分构造出2个矩形和1个正方形（如图），则阴影部分的面积是．

查看试题解析
14. 如图，在四边形ABCD中，∠BAD=∠CDA=90°，AB=1，CD=2，过A，B，D三点的⊙O分别交BC，CD于点E，M，下列结论：①DM=CM；② $\overset{⌢}{A B} = \overset{⌢}{E M}$ ；③⊙O的直径为2；④AE=AD．其中正确的结论有（填序号）．

查看试题解析
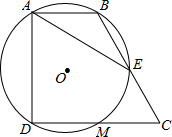15. 如图，四边形ABCD是⊙O的内接四边形，已知AC⊥BD ，垂足为E ， OF⊥AB于F ．

(1)、若AF＝OF ，则∠ADB的度数为；

(2)、若⊙O的半径为5，AB＝8，则CD的长为．

查看试题解析
16. 如图1所示是一款带毛刷的圆形扫地机器人，它的俯视图如图2所示，毛刷的一端为固定点 $P$ ，另一端为点 $C ， C P = 8 cm$ ，毛刷绕着点 $P$ 旋转形成的圆弧交 $⊙ O$ 于点A，B，且A，P，B三点在同一直线上．当毛刷 $P C$ 从 $P A$ 出发顺时针扫过 $60 °$ 时， $P C ∥ O A$ ，则 $⊙ O$ 的半径为 $cm$ ，毛刷在旋转过程中，与 $⊙ O$ 交于点 $D$ ，则 $C D$ 的最大长度为 $cm$ ．

查看试题解析

三、综合题

17. 如图，四边形ABCD内接于 $⊙ O$ ，对角线AC是 $⊙ O$ 的直径，BD平分 $∠ A B C, B D$ 交AC于点 $E$ ，过点 $D$ 作 $D F ⊥ D B, D F$ 交 $⊙ ◯$ 于点 $H$ ，交BA延长线于点 $F$ .

(1)、求 $∠ F H A$ 的度数.

(2)、求证： $A F = C B$ .

(3)、过点 $F$ 作 $F G / / B D$ 交CA延长线于点 $G$ ，求证： $F G^{2} + B E^{2} = 2 A G^{2}$ .

查看试题解析
18. 如图，在Rt $△ A B C$ 中， $∠ A C B = 9 0^{°}, B C$ 是 $⊙ O$ 的直径， $⊙ O$ 与边AB交于点D，E为BD的中点，连接CE，与AB交于点 $F$ .

(1)、若 $∠ A = 4 ∠ B$ ，求 $∠ E C B$ 的大小；

(2)、求证： $A C = A F$ ；

(3)、若 $B C = 6, \frac{E F}{F C} = \frac{1}{2}$ ，求 $△ A F C$ 的面积.

查看试题解析
19. 如图， $A B$ 是 $⊙ O$ 的直径，D、E为 $⊙ O$ 上位于 $A B$ 异侧的两点，连接 $B D$ 并延长至点C，使得 $C D = B D$ ，连接 $A C$ 交 $⊙ O$ 于点F，连接 $A E$ 、 $D E$ 、 $D F$ ．

(1)、证明： $A B = A C$ ；

(2)、若 $∠ E = 50 °$ ，求 $∠ B D F$ 的度数；

(3)、设E是半圆 $A E B$ 的中点， $D E$ 交 $A B$ 于点G，若 $D F = 6$ ， $A B = 10$ ，求 $D G$ 的长．

查看试题解析
20. 如图1，AB是 $⊙ O$ 的直径，点 $D$ 为AB下方 $⊙ O$ 上一点.点 $C$ 为 $\overset{⏜}{A B D}$ 的中点，连结CD，CA，AD

(1)、求证：OC平分 $∠ A C D$ .

(2)、如图2，延长AC，DB相交于点 $E$ .
①求证： $O C / / B E$ .
②若 $C E = 4 \sqrt{5}, B D = 6$ ，求 $⊙ O$ 的半径.

查看试题解析
21. 如图，四边形 $A B C D$ 内接于 $⊙ O ， B D$ 为直径， $\overset{⌢}{A D}$ 上存在点 $E$ ，满足 $\overset{⌢}{A E} = \overset{⌢}{C D}$ ，连结 $B E$ 并延长交 $C D$ 的延长线于点 $F ， B E$ 与 $A D$ 交于点 $G$ ．

(1)、设 $∠ D B C = α$ ，请用含 $α$ 的代数式表示 $∠ F G D$ ．

(2)、若 $B D = C F$ ，求证： $E F = D G$ ．

(3)、在（2）的条件下，若 $∠ D B C = 30 °$ ，则 $\frac{S_{△ D G F}}{S_{△ C E F}}$ 的值为_______．（直接写出答案）

查看试题解析
22. 定义：同一个圆中，互相垂直且相等的两条弦叫做等垂弦，等垂弦所在直线的交点叫做等垂点．

(1)、如图1， $A B$ 、 $A C$ 是 $⊙ O$ 的等垂弦， $O D ⊥ A B$ ， $O E ⊥ A C$ 垂足分别为D，E．
求证：四边形 $A D O E$ 是正方形；

(2)、如图2， $A B$ 是 $⊙ O$ 的弦，作 $O D ⊥ O A$ ， $O C ⊥ O B$ 分别交 $⊙ O$ 于D，C两点，连接 $C D$ ．分别交 $A B$ 、 $O A$ 与点 $M$ 、点 $E$ ．
求证： $A B$ ， $C D$ 是 $⊙ O$ 的等垂弦；

(3)、已知 $⊙ O$ 的直径为10， $A B$ 、 $C D$ 是 $⊙ O$ 的等垂弦，P为等垂点．若 $A P = 3 B P$ ．求 $A B$ 的长．

查看试题解析
23. 如图1， $△ A B C$ 内接于 $⊙ O, A B = A C = 10, B C = 12$ ，点 $E$ 为 $\overset{⌢}{A C}$ 上一点，点 $F$ 为 $\overset{⌢}{C E}$ 的中点，连结BF并延长与AE交于点 $G$ ，连结AF，CF

(1)、求证： ∠AFC=∠AFG

(2)、如图 2，当 BG 经过圆心0时，
①求 FG 的长；.
②记△AFG，△BFC的面积分别为 $S_{1}, S_{2}$ ，则 $S_{1} : S_{2} =$ .

查看试题解析
24. 如图，四边形ABCD内接于 $⊙ O, B D$ 为直径，AD上存在点 $E$ ，满足 $\overset{⏜}{A E} = \overset{⏜}{C D}$ ，连结BE并延长交CD的延长线于点F，BE与AD交于点 $G$ .

(1)、设 $∠ D B C = α$ ，请用含 $α$ 的代数式表示 $∠ F G D$ .

(2)、若 $B D = C F$ ，求证： $E F = D G$ .

(3)、在（2）的条件下，若 $∠ D B C = 3 0^{°}$ ，则 $\frac{S_{△ D G F}}{S_{△ C E F}}$ 的值为（直接写出答案）

查看试题解析
25. 如图，已知 $△ A B C$ 内接于 $⊙ O$ ，点C在劣弧 $A B$ 上（不与点A ， B重合），点D为弦 $B C$ 的中点， $D E ⊥ B C, D E$ 与 $A C$ 的延长线交于点E ，射线 $A O$ 与射线 $E B$ 交于点F ，与 $⊙ O$ 交于点G ，设 $∠ G A B = α, ∠ A C B = β$ ， $∠ E A G + ∠ E B A = γ$ ，

(1)、点点同学通过画图和测量得到以下近似数据：
$α$
$30 °$
$40 °$
$50 °$
$60 °$
$β$
$120 °$
$130 °$
$140 °$
$150 °$
$γ$
$150 °$
$140 °$
$130 °$
$120 °$
猜想： $β$ 关于 $α$ 的函数表达式， $γ$ 关于 $α$ 的函数表达式．

(2)、对（1）中的两个结论给出证明．

(3)、若 $γ = 135 °$ ， $C D = 3, △ A B E$ 的面积为 $△ A B C$ 的面积的4倍，求 $⊙ O$ 半径的长．

查看试题解析
26. 如图1， $△ A B C$ 是 $⊙ O$ 的内接三角形，点 $D$ 在 $⊙ O$ 上， $A$ 是弧BD的中点，点 $E$ 在BC上，连接BD、AE，BD与AE于点 $F$ ， $∠ A E B = ∠ B A C$ ．

(1)、求证： $A F = B F$ ；

(2)、如图2，延长AE交 $⊙ O$ 于点 $G$ ，连接AO，交BD于点 $H$ ，求证： $A G = 2 D H$ ；

(3)、如图3，在（2）的条件下，作直径BM交AG于点 $K$ ，连接AM交BD于点 $N$ ，当AC是 $⊙ O$ 的直径时， $M N = 2 \sqrt{5} K F$ ， $E G = 3$ ，求弦BC的长．

查看试题解析
27. 如图1，已知四边形ABCD内接于⊙O，AD＝BC，延长AB到E，使BE＝AB，连接EC，F是EC的中点，连接BF．

(1)、若⊙O的半径为2，∠DAB＝120°，求劣弧 $\overset{⌢}{B D}$ 的长；

(2)、如图2，连接BD，求证：∠DBA＝∠FBE；

(3)、如图3，G是BD的中点，过B作AE的垂线交⊙O于点P，连接PG，PF，求证：PG＝PF．

查看试题解析
28. 已知AB是⊙O直径，点C为⊙O上一点，连结AC、BC ．

(1)、如图1，若∠CBP＝∠ABC ， CB＝CP ，连结PC ，判断∠BCP和∠BAC的数量关系，并证明．

(2)、如图2，若∠CBP＝∠ABC ， PC＝PB ，连结PC并延长交⊙O于点E ，连结BF交AC于点E ．若AC＝8，BC＝6，求BE∙BF的值．

(3)、如图3，点C为AB的中点，已知CF＝CA ，过点B作 $B Q ∥ A C$ 与CF交与点Q ，连结AF交BC于点K ，求BQ、FQ、BK之间的数量关系．

查看试题解析

四、实践探究题

29. 探究与实践：“善思”小组开展“探究四点共圆的条件”活动，得出结论：对角互补的四边形四个顶点共圆．该小组继续利用上述结论进行探究．
【提出问题】如图 $1$ ，在线段 $A C$ 同侧有两点 $B$ ， $D$ ，连接 $A D$ ， $A B$ ， $B C$ ， $C D$ ，如果 $∠ B = ∠ D$ ，那么 $A$ ， $B$ ， $C$ ， $D$ 四点在同一个圆上．
【探究展示】如图 $2$ ，作经过点 $A$ ， $C$ ， $D$ 的 $⊙ O$ ，在劣弧 $A C$ 上取一点 $E$ （不与 $A$ ， $C$ 重合），连接 $A E$ ， $C E$ ，
则 $∠ A E C + ∠ D = 180 °$ （依据 $1$ ）
∵ $∠ B = ∠ D$ ，
∴ $∠ A E C + ∠ B = 180 °$ ，
∴点 $A$ ， $B$ ， $C$ ， $E$ 四点在同一个圆上（对角互补的四边形四个顶点共圆）
∴点 $B$ ， $D$ 都在点 $A$ ， $C$ ， $E$ 所确定的 $⊙ O$ 上（依据 $2$ ）
∴点 $A$ ， $B$ ， $C$ ， $E$ 四点在同一个圆上；
【反思归纳】
$①$ 圆内接四边形对角互补；
$②$ 对角互补的四边形四个顶点共圆；
$③$ 过不在同一直线上的三个点有且只有一个圆；
$④$ 同圆中，同弧所对的圆周角相等；
（ $1$ ）上述探究过程中的“依据 $1$ ”、“依据 $2$ ”分别是指什么？依据 $1$ ：；依据 $2$ ：．（从框内选一个选项，直接填序号）
（ $2$ ）如图 $3$ ，在四边形 $A B C D$ 中， $∠ 1 = ∠ 2 = 70 °$ ， $∠ 3 = 45 °$ ，则 $∠ 4$ 的度数为；
【拓展探究】
（ $3$ ）如图4，已知 $△ A B C$ 是等腰三角形， $A B = A C$ ，点 $D$ 在 $B C$ 上（不与 $B C$ 的中点重合），连接 $A D$ ．作点 $C$ 关于 $A D$ 的对称点 $E$ ，连接 $E B$ 并延长交 $A D$ 的延长线于 $F$ ，连接 $A E$ ， $D E$ ．
$①$ 求证： $A$ ， $D$ ， $B$ ， $E$ 四点共圆；
$②$ 若 $A B = 2 \sqrt{2}$ ， $A D \cdot A F$ 的值是否会发生变化，若不变化，求出其值；若变化，请说明理由．

查看试题解析

$α$	$30 °$	$40 °$	$50 °$	$60 °$
$β$	$120 °$	$130 °$	$140 °$	$150 °$
$γ$	$150 °$	$140 °$	$130 °$	$120 °$