《三角形的综合》精选压轴题(三)—2025年浙江省八(上)数学期中复习
试卷更新日期:2025-10-19 类型:复习试卷
一、单选题
-
1. 如图,四个全等的直角三角形与中间的小正方形拼成了一个大正方形 , 连接 , 交于点 , 若正方形的面积为30, . 则的值是( )
 A、 B、 C、7 D、2. 如图,在中, , , , 点 , , 分别在边 , , 上,连结 , . 已知点和点关于直线对称.若 , 则的长为( )
A、 B、 C、7 D、2. 如图,在中, , , , 点 , , 分别在边 , , 上,连结 , . 已知点和点关于直线对称.若 , 则的长为( ) A、 B、 C、 D、3. 如图,中,的角平分线交于点P,延长 , , 则下列结论中正确的是( )
A、 B、 C、 D、3. 如图,中,的角平分线交于点P,延长 , , 则下列结论中正确的是( )①平分;
②;
③;
④ .
 A、①②④ B、①③④ C、②③④ D、①②③④4. 如图,在中, , 为斜边的中点,在内绕点转动,分别边、于点、(点不与点、重合),下列说法正确的是( )
A、①②④ B、①③④ C、②③④ D、①②③④4. 如图,在中, , 为斜边的中点,在内绕点转动,分别边、于点、(点不与点、重合),下列说法正确的是( )①;
②;
③ .
 A、①② B、①③ C、②③ D、①②③5. 如图,正方形中,点 , , , 分别在边 , , , 上,且 , 依次连接 , , , , 将和分别沿 , 翻折,使点 , 分别落在和处,连接和 . 若 , 的面积为 , 则正方形的面积为( )
A、①② B、①③ C、②③ D、①②③5. 如图,正方形中,点 , , , 分别在边 , , , 上,且 , 依次连接 , , , , 将和分别沿 , 翻折,使点 , 分别落在和处,连接和 . 若 , 的面积为 , 则正方形的面积为( ) A、10 B、9 C、8 D、76. 如图,已知和都是等腰直角三角形, , , 交于点F,连接 , 下列结论:①;②;③;④平分;⑤ , 其中结论正确的序号是( )
A、10 B、9 C、8 D、76. 如图,已知和都是等腰直角三角形, , , 交于点F,连接 , 下列结论:①;②;③;④平分;⑤ , 其中结论正确的序号是( ) A、①②③④ B、①②④⑤ C、①③④⑤ D、①②③⑤7. 如图,在中, , D,E分别为线段 , 上一点,且 , 连接、交于点G,延长交于点F.以下四个结论正确的是( )
A、①②③④ B、①②④⑤ C、①③④⑤ D、①②③⑤7. 如图,在中, , D,E分别为线段 , 上一点,且 , 连接、交于点G,延长交于点F.以下四个结论正确的是( )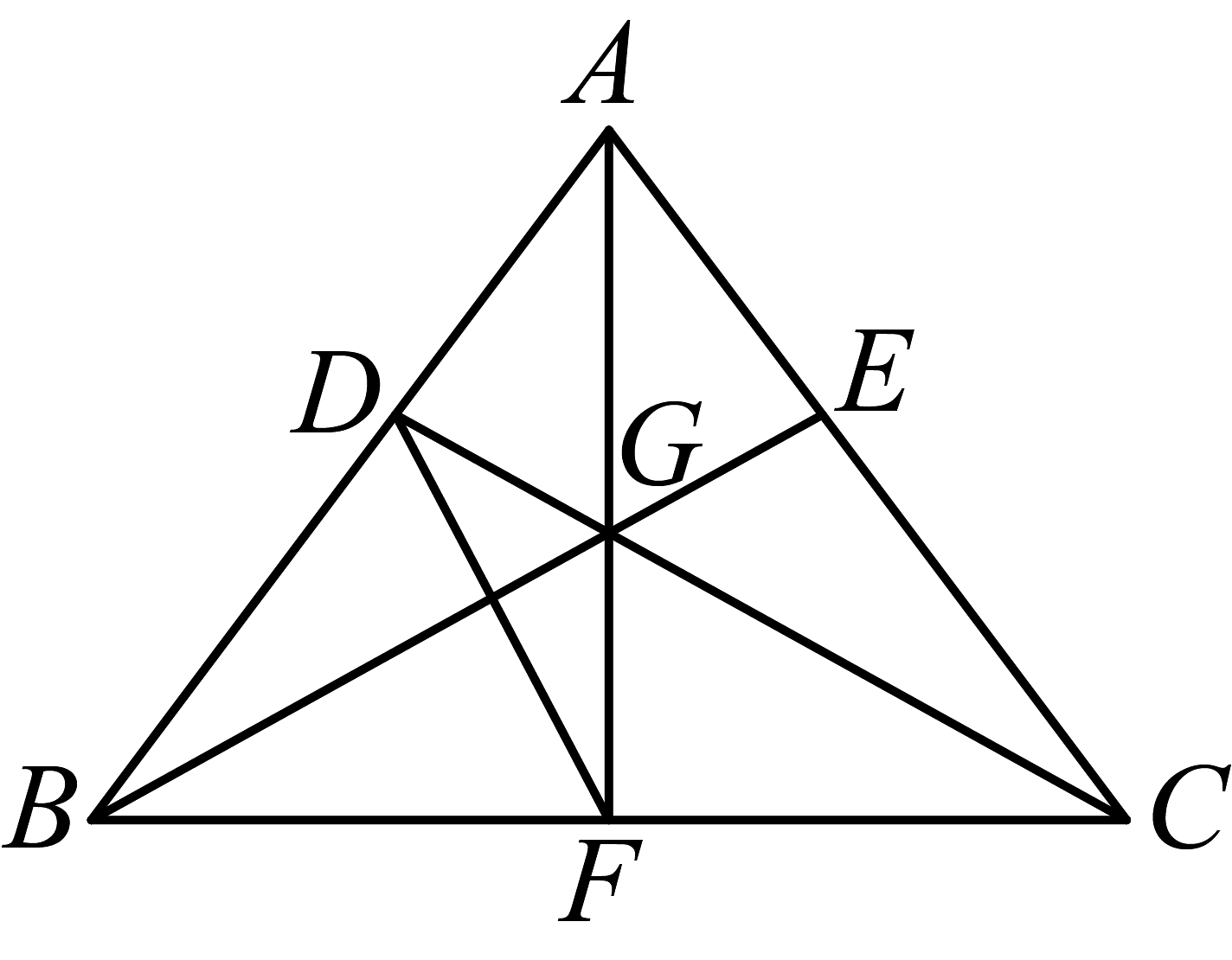
①;
②若 , 则;
③连结 , 若 , 则;
④若平分 , 则
A、①②③ B、③④ C、①②④ D、①②③④8. 如图,是的角平分线, , , , , 分别是和上的任意一点;连接 , , , , 给出下列结论:①的面积是12;②;③的最小值是;④若平分 , 则的面积为9.其中正确的是( ) A、①② B、①②④ C、①③ D、②③④9. 如图,等腰中, , , 于点 , 的平分线分别交、于、两点,为的中点,的延长线交于点 , 连接 , 下列结论:①;②;③;④;⑤平分 , 其中正确结论有( )
A、①② B、①②④ C、①③ D、②③④9. 如图,等腰中, , , 于点 , 的平分线分别交、于、两点,为的中点,的延长线交于点 , 连接 , 下列结论:①;②;③;④;⑤平分 , 其中正确结论有( ) A、5个 B、4个 C、3个 D、2个
A、5个 B、4个 C、3个 D、2个二、填空题
-
10. 如图,在中, , 点 , 分别在 , 上,且 , 将沿折叠,点恰好落在边上的点处,与交于点 . 下列结论:其中正确的结论有 . (填序号)
;
若 , 则;
若 , , 则;
若 , , 则 .
 11. 如图,点P是在正内一点. , , , 将线段绕点A逆时针旋转得到线段 , 连接、 , 四边形的面积为 .
11. 如图,点P是在正内一点. , , , 将线段绕点A逆时针旋转得到线段 , 连接、 , 四边形的面积为 . 12. 在中, , , 点是边上的点,将沿折叠得到 , 点是点的对称点.若 , 则的长是 .
12. 在中, , , 点是边上的点,将沿折叠得到 , 点是点的对称点.若 , 则的长是 . 13. 如图,中,于点平分 , 交于点E,于点F,且交于点G,若 , 则 , .
13. 如图,中,于点平分 , 交于点E,于点F,且交于点G,若 , 则 , . 14. 如图,在中, , , 平分 , 交于 , 点是上的一点,且 , 连交于 , 连 , 下列结论: , , , , 其中正确的有 .
14. 如图,在中, , , 平分 , 交于 , 点是上的一点,且 , 连交于 , 连 , 下列结论: , , , , 其中正确的有 . 15. 如图,已知在中, , , , 是上的一点, , 点从点出发沿射线方向以每秒2个单位的速度向右运动,设点的运动时间为 . 过点作于点 . 在点P的运动过程中,当t为时,能使?
15. 如图,已知在中, , , , 是上的一点, , 点从点出发沿射线方向以每秒2个单位的速度向右运动,设点的运动时间为 . 过点作于点 . 在点P的运动过程中,当t为时,能使? 16. 如图,在中, , , 分别以 , 为边在外作等边和等边 , 连结 , .
16. 如图,在中, , , 分别以 , 为边在外作等边和等边 , 连结 , .
(1) , 则;
(2)若 , 则的长为 .
17. 一副三角板如图叠放, , , 互相平分于点O,点F在边上,边交于点H,边交于点G.(1);
(2)若 , 则(用含a的代数式表示).

三、综合题
-
18. 如图,在等腰中, , P是线段上的一个动点(与点B,C不重合),连接 , 延长至点Q,使得 , 过点Q作于点H,交于点N,交于点M,连结 .
 (1)、若 , 求的度数.(用含α的式子表示);(2)、求证:;(3)、在P点运动过程中线段与的比值是否发生变化?若不变请计算它们的比值.19. 如图, 在RtABC 中AB=10,BC⊥AC,P为线段AC上一点,点Q,P 关于直线BC对称,QD⊥AB于点D,DQ与BC交于点 E,连结DP, 设AP=m.
(1)、若 , 求的度数.(用含α的式子表示);(2)、求证:;(3)、在P点运动过程中线段与的比值是否发生变化?若不变请计算它们的比值.19. 如图, 在RtABC 中AB=10,BC⊥AC,P为线段AC上一点,点Q,P 关于直线BC对称,QD⊥AB于点D,DQ与BC交于点 E,连结DP, 设AP=m.(1) 若BC=8,求AC的长,并用含m的代数式表示PQ的长;
(2)在(1)的条件下,若AP=PD.求CP的长:
(3)连结PE, 若∠A=60°,PCE与PDE的画积之比为1:2,求m的值.
 20. 如图,在等腰直角三角形中, , , 点在边上,作于点 , 连接、 .
20. 如图,在等腰直角三角形中, , , 点在边上,作于点 , 连接、 .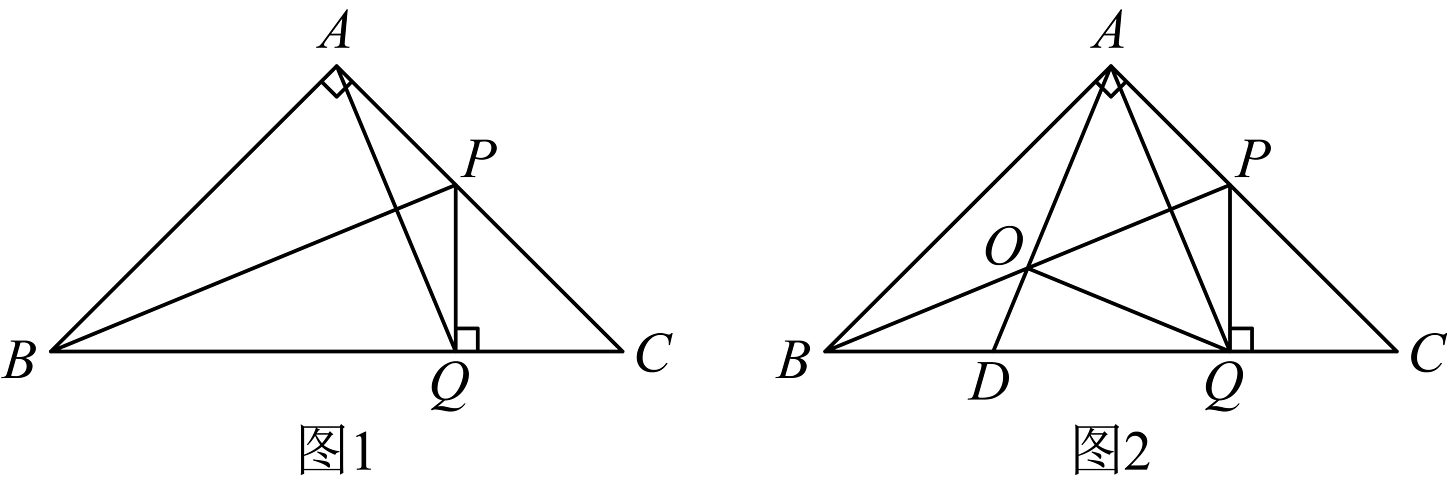 (1)、如图1,若平分 , 求证:垂直平分 .(2)、如图2,点是的中点,直线交于点 , 连接 ,
(1)、如图1,若平分 , 求证:垂直平分 .(2)、如图2,点是的中点,直线交于点 , 连接 ,①求证:是等腰直角三角形.
②若 , , 求的长度.
21. (1)已知点D为等边边所在直线上一点,连 , 以为边作等边 , 连 .①如图1,点D在线段上,求证:;
②当点D在的延长线上,①中的结论是否仍然成立,请画出图形判断并说明理由;
(2)如图2,点D为等腰直角直角边所在直线上任意一点,连 , 以为斜边作等腰直角 , 连 , 当的长最小时,直接写出的值,不需要说明理由.
 22. 已知在直角三角形中, , D为斜边中点,C为边上一点.
22. 已知在直角三角形中, , D为斜边中点,C为边上一点. (1)、 .(2)、如图1,连结交于点E.当时:
(1)、 .(2)、如图1,连结交于点E.当时:①求证:;
②求的面积.
(3)、如图2,连结 , 将沿着折叠得到 . 当与的一边平行时,求的长度.23. 在中, , , D为边上一点. (1)、如图1,若 , , 求的面积;(2)、如图2,作 , 且 , 连结交边于点F,连结 .
(1)、如图1,若 , , 求的面积;(2)、如图2,作 , 且 , 连结交边于点F,连结 .①若 , 求证:;
②若 , 写出线段 , , 长度之间的等量关系,并说明理由.
24. 中, , , 是边一点,连接 , 为射线上一点. (1)、如图1,当点在边上时,连接 . 交于点 , 若 .
(1)、如图1,当点在边上时,连接 . 交于点 , 若 .①与相等吗?请判断并说明理由;
②若 , , 求的长.
(2)、如图2,当点在延长线上时,连接 , 若 .①探究线段 , , 的数量关系并说明理由;
②连接 , 求的值.
25. 如图,已知等边 , 点为内的一点,连接、、 , , 以为边向上方作等边 , 连接().(1)求证:≌
(2)若 , , 则的面积为 .
(3)若 , , (为大于1的整数).求证:.
 26. 如图1,直线 , 平分 , 过点B作交于点C;动点E、D同时从A点出发,其中动点E以的速度沿射线方向运动,动点D以的速度沿射线方向运动;已知 , 设动点D,E的运动时间为t.
26. 如图1,直线 , 平分 , 过点B作交于点C;动点E、D同时从A点出发,其中动点E以的速度沿射线方向运动,动点D以的速度沿射线方向运动;已知 , 设动点D,E的运动时间为t. (1)、求的度数;(2)、当点D在射线上运动时满足 , 求点D,E的运动时间t的值;(3)、当动点D在射线上运动,点E在射线上运动过程中,是否存在某个时间t,使得与全等?若存在,请求出此时的长;若不存在,请说明理由.27. 如图1,是等边内一点,连结 . 将线段绕点顺时针旋转得到线段 , 连结 .
(1)、求的度数;(2)、当点D在射线上运动时满足 , 求点D,E的运动时间t的值;(3)、当动点D在射线上运动,点E在射线上运动过程中,是否存在某个时间t,使得与全等?若存在,请求出此时的长;若不存在,请说明理由.27. 如图1,是等边内一点,连结 . 将线段绕点顺时针旋转得到线段 , 连结 . (1)、求证: .(2)、如图2,连结 .
(1)、求证: .(2)、如图2,连结 .①当 , 且为等腰三角形时,求出的度数.
②当 , 且时,请直接写出点到点的距离.
28. 在中, , 点B在边上,且 , C是射线上的一个动点(不与点B重合,且),在射线上截取 , 连接 . (1)、当点C在线段上时,
(1)、当点C在线段上时,①若点C与点D重合,请根据题意补全图1,并直接写出线段与的数量关系为 ;
②如图2,若点C不与点D重合,请证明;
(2)、当点C在线段的延长线上时,用等式表示线段 , , 之间的数量关系(直接写出结果,不需要证明).29. 在中, , 点D是直线上一点(不与B,C重合),以为一边在的右侧作 , 使 , , 连接 . (1)、如图1,当点D在线段上时,如果 , 则 °.(2)、设 .
(1)、如图1,当点D在线段上时,如果 , 则 °.(2)、设 .①如图2,当点D在线段上移动时,α、β之间有怎样的数量关系?请说明理由.
②当点D在直线上移动时,α、β之间有怎样的数量关系?请你在备用图上画出图形,并直接写出结论.
30. 如图,四边形中, , , 是的中点. (1)、如图①,连接 , , 若 , 求的度数;(2)、如图②,连接交于点 , 若 , , 求的长;(3)、如图③,作于点 , 试探究线段 , , 之间的数量关系,并说明理由.31. 根据以下素材,探索解决问题.
(1)、如图①,连接 , , 若 , 求的度数;(2)、如图②,连接交于点 , 若 , , 求的长;(3)、如图③,作于点 , 试探究线段 , , 之间的数量关系,并说明理由.31. 根据以下素材,探索解决问题.如何作出“倍角三角形”?
素材
如果一个三角形的一个内角等于另一个内角的两倍,则称这样的三角形为“倍角三角形”
问题解决
项目操作
如图 , 中, , , 请将分成两个小三角形,使得其中一个小三角形是“倍角三角形”,并标注该“倍角三角形”三个内角的度数.

项目探索
若是倍角三角形, , , , 求面积.
项目拓展
如图 , 的外角平分线与的延长线相交于点 , 点在延长线上,若 , , 请你找出图中的倍角三角形,并进行证明.
