《三角形的综合》精选压轴题(二)—2025年浙江省八(上)数学期中复习
试卷更新日期:2025-10-19 类型:复习试卷
一、单选题
-
1. 在Rt△ABC中,∠C=90°,点P在边AB上.BC=6, AC=8, ( )A、若∠ACP=45°, 则CP=5 B、若∠ACP=∠B,则CP=5 C、若∠ACP=45°,则CP= D、若∠ACP=∠B,则CP=2. 如图,在锐角三角形中, , 边上的中线 . 过点A作于点E,记的长为a,的长为b.当a,b的值发生变化时,下列代数式的值不变的是( )
 A、 B、 C、 D、3. 如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( )
A、 B、 C、 D、3. 如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( ) A、140° B、100° C、50° D、40°4. 如图,四边形中, , 的角平分线与点D,E为的中点,则与面积之差的最大值为( )
A、140° B、100° C、50° D、40°4. 如图,四边形中, , 的角平分线与点D,E为的中点,则与面积之差的最大值为( ) A、9 B、4.5 C、3 D、1.55. 如图,和均为等边三角形,且点B,C,D在同一直线上,交于点G,交于点H,连结 . 则下列结论中正确的有( )
A、9 B、4.5 C、3 D、1.55. 如图,和均为等边三角形,且点B,C,D在同一直线上,交于点G,交于点H,连结 . 则下列结论中正确的有( )(1);(2);(3);(4)平分;(5)是等边三角形.
 A、2个 B、3个 C、4个 D、5个6. 如图,是的角平分线, , , , P,Q分别是和上的任意一点,连接 , , , , 给出下列结论:
A、2个 B、3个 C、4个 D、5个6. 如图,是的角平分线, , , , P,Q分别是和上的任意一点,连接 , , , , 给出下列结论:①;
②;
③的最小值是;
④若平分 , 则的面积为9.
其中正确的是( )
 A、①②③ B、①②④ C、①③④ D、②③④7. 如图,在△ABC中,∠ACB=60°,AG平分∠BAC交BC与点G , BD平分∠ABC交AC于点D , AG、BD相交于点F , BE⊥AG交AG的延长线于点E , 连接CE , 下列结论中正确的是( )
A、①②③ B、①②④ C、①③④ D、②③④7. 如图,在△ABC中,∠ACB=60°,AG平分∠BAC交BC与点G , BD平分∠ABC交AC于点D , AG、BD相交于点F , BE⊥AG交AG的延长线于点E , 连接CE , 下列结论中正确的是( )
①若∠BAD=70°,则∠EBC=5°;②BF=2EF;③BE=CE;④AB=BG+AD .
A、4个 B、3个 C、2个 D、1个8. 如图,在和中, , , , 过作 , 垂足为 , 交的延长线于点 , 连接 . 四边形的面积为64, . 则的长是( ) A、8 B、 C、 D、69. 如图,点是正方形的对角线上一点,于点 , 于点 , 连接 , 给出下列四个结论:①;②;③;④ . 其中正确的有( )
A、8 B、 C、 D、69. 如图,点是正方形的对角线上一点,于点 , 于点 , 连接 , 给出下列四个结论:①;②;③;④ . 其中正确的有( ) A、1个 B、2个 C、3个 D、4个10. 如图,在中, , , 的平分线分别交、于点D、E,、相交于点F,连接 . 下列结论:①;②;③;④点F到三边的距离相等;⑤ . 其中错误的结论有( )
A、1个 B、2个 C、3个 D、4个10. 如图,在中, , , 的平分线分别交、于点D、E,、相交于点F,连接 . 下列结论:①;②;③;④点F到三边的距离相等;⑤ . 其中错误的结论有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图,已知在中, , , , 是上的一点, , 点从点出发沿射线方向以每秒2个单位的速度向右运动.设点的运动时间为 . 过点作于点 . 在点的运动过程中,当为时,能使?
 12. 如图,在中,是边上的高线,是边上的中线,于点G,且 . 若 , 则的度数是 .
12. 如图,在中,是边上的高线,是边上的中线,于点G,且 . 若 , 则的度数是 .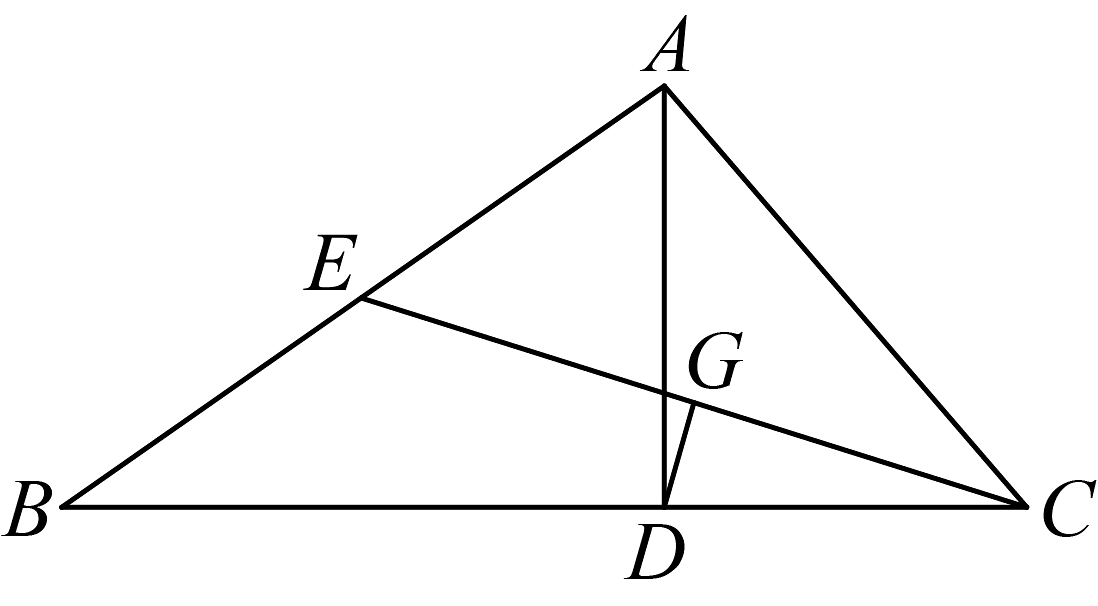 13. 在中, , 将一块足够大的直角三角尺按如图所示放置,顶点在线段AB上滑动,PM始终经过点 , 斜边PN交AC于点.在点滑动过程中,为等腰三角形时,则点与点的距离BP为.
13. 在中, , 将一块足够大的直角三角尺按如图所示放置,顶点在线段AB上滑动,PM始终经过点 , 斜边PN交AC于点.在点滑动过程中,为等腰三角形时,则点与点的距离BP为. 14. 如图所示,在等腰中, , 点为射线上的动点, , 且 , 与所在的直线交于点 , 若 , 则 .
14. 如图所示,在等腰中, , 点为射线上的动点, , 且 , 与所在的直线交于点 , 若 , 则 . 15. 如图,在中, , 点D,E,F分别是线段的中点,下列结论:①为等边三角形.② . ③ . ④ . 其中正确的是 .
15. 如图,在中, , 点D,E,F分别是线段的中点,下列结论:①为等边三角形.② . ③ . ④ . 其中正确的是 . 16. 如图,中, , 点D是上一动点,将沿折叠得到 , 当与重叠部分是直角三角形时,的度数为 .
16. 如图,中, , 点D是上一动点,将沿折叠得到 , 当与重叠部分是直角三角形时,的度数为 . 17. 如图,在中, , 点在内,平分 , 连接 , 把沿折叠,落在处交于 , 恰有若 , , 则 .
17. 如图,在中, , 点在内,平分 , 连接 , 把沿折叠,落在处交于 , 恰有若 , , 则 . 18. 如图,在等腰中,于点 , 点和分别在线段和线段上,连结 , 则平分 , 且满足 , 若 , 则的面积为 .
18. 如图,在等腰中,于点 , 点和分别在线段和线段上,连结 , 则平分 , 且满足 , 若 , 则的面积为 . 19. 如图,已知和均为等边三角形,点O是的中点,点D在射线上,连结 , 则 , 若 , 则的最小值= .
19. 如图,已知和均为等边三角形,点O是的中点,点D在射线上,连结 , 则 , 若 , 则的最小值= . 20. 如图,在中, , 分别以AB , AC为边在外作等边和等边 , 连结BE , CD.
20. 如图,在中, , 分别以AB , AC为边在外作等边和等边 , 连结BE , CD. (1)、 , 则;(2)、若 , 则CD的长为.
(1)、 , 则;(2)、若 , 则CD的长为.三、综合题
-
21. 在中, , 于点 , 点E,F分别在AC,BC上,且与CD交于点.
 (1)、如图1,当点与点重合时,
(1)、如图1,当点与点重合时,①求证:;②直接写出的值.
(2)、如图2,当点在AC边上时①依题意补全图2;②的值是否发生变化,请说明理由.
22. 在中, , , 是的中点.点是上的点,将沿所在的直线对折,记点的对应点为 . (1)、当时,求的度数.(2)、当点落在的一边上时,求的度数.(3)、当点落在直线上方,且对折后重叠部分为等腰三角形时,求的度数.23. 如图1,已知在中, , 已知 , . 是边上一动点,连接 , 以为对称轴将翻折至 .
(1)、当时,求的度数.(2)、当点落在的一边上时,求的度数.(3)、当点落在直线上方,且对折后重叠部分为等腰三角形时,求的度数.23. 如图1,已知在中, , 已知 , . 是边上一动点,连接 , 以为对称轴将翻折至 . (1)、若时.
(1)、若时.①求证:;
②求折痕的长.
(2)、如图2,若时,以为原点,直线为轴,建立平面直角坐标系,求此时的坐标.24. 如图1,直线AM⊥AN,AB平分∠MAN,过点B作BC⊥BA交AN于点C;动点E、D同时从A点出发,其中动点E以2cm/s的速度沿射线AN方向运动,动点D以1cm/s的速度沿射线AM方向运动;已知AC=6cm,设动点D,E的运动时间为t. (1)、求∠ACB的度数;(2)、当点D在射线AM上运动时满足AD:CE=2:3,求点D,E的运动时间的值:(3)、当动点D在射线AM上运动,点E在射线AN上运动过程中,是否存在某个时间,使得△ADB与△BEC全等?若存在,请求出此时BD的长:若不存在,请说明理由.25. 如图1是实验室中的一种摆动装置,BC在地面上,支架ABC是底边长为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕D旋转,AD=4,DM=3.
(1)、求∠ACB的度数;(2)、当点D在射线AM上运动时满足AD:CE=2:3,求点D,E的运动时间的值:(3)、当动点D在射线AM上运动,点E在射线AN上运动过程中,是否存在某个时间,使得△ADB与△BEC全等?若存在,请求出此时BD的长:若不存在,请说明理由.25. 如图1是实验室中的一种摆动装置,BC在地面上,支架ABC是底边长为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕D旋转,AD=4,DM=3.
(1) 在旋转过程中,
①当A,D,M三点在同一直线上时,求AM的长;
②当A,D,M三点为同一直角三角形的顶点时,求AM的长;
(2) 当摆动臂AD顺时针旋转 , 点D的位置由外的点D1转到其内的点D2处,连接D1D2如图2,此时∠AD2C= , CD2= , 求BD2的长.
26. 如图1,过△ABC的顶点A分别作对边BC上的中线AD和高线AE . (1)、在图1中,若AB=15,AC=13,BC=14,BE=a , 分别求出a , 的值;(2)、①如图1,猜想和之间的关系,并证明你的结论;
(1)、在图1中,若AB=15,AC=13,BC=14,BE=a , 分别求出a , 的值;(2)、①如图1,猜想和之间的关系,并证明你的结论;②如图2,∠MON=45°,点P是边OM上一动点,点Q是边ON上一点,且OQ=8, 则的最小值为 ▲ .
27. 如图,于点 , 连接 , , , , 点在线段上运动时(不与A,重合),点在线段上,满足 , 连接 . 当为中点时,恰好与点重合. (1)、求的长.(2)、若 , 运动到中点时,求证:直线 .(3)、连接 , 当是等腰三角形时,请写出所有符合条件的的长.28. 如图,已知等边 , 点为内的一点,连接.以CD为边向CD上方作等边 , 连接AE().
(1)、求的长.(2)、若 , 运动到中点时,求证:直线 .(3)、连接 , 当是等腰三角形时,请写出所有符合条件的的长.28. 如图,已知等边 , 点为内的一点,连接.以CD为边向CD上方作等边 , 连接AE(). (1)、求证:.(2)、若 , 则的面积为.(3)、若(为大于1的整数).求证:.29. 在∆ABC中, ∠ACB=90°,AC=BC, D为边AB上一点.
(1)、求证:.(2)、若 , 则的面积为.(3)、若(为大于1的整数).求证:.29. 在∆ABC中, ∠ACB=90°,AC=BC, D为边AB上一点. (1)、如图1,若AC= , AD=3, 求∆CDB的面积;(2)、如图2, 作DE⊥CD, 且DE=CD, 连结 CE交边AB 于点F, 连结BE.
(1)、如图1,若AC= , AD=3, 求∆CDB的面积;(2)、如图2, 作DE⊥CD, 且DE=CD, 连结 CE交边AB 于点F, 连结BE.①若BC=BD,求证: ∠ADC=∠BED;
②若BD>BC, 写出线段 BC, BE, CE 长度之间的等量关系,并说明理由
30. 某兴趣小组在学习了勾股定理之后提出:“锐(钝)角三角形有没有类似于勾股定理的结论”的问题.首先定义了一个新的概念:如图(1)中,是的中点,是射线上的点,设 . 若 , 则称为勾股比.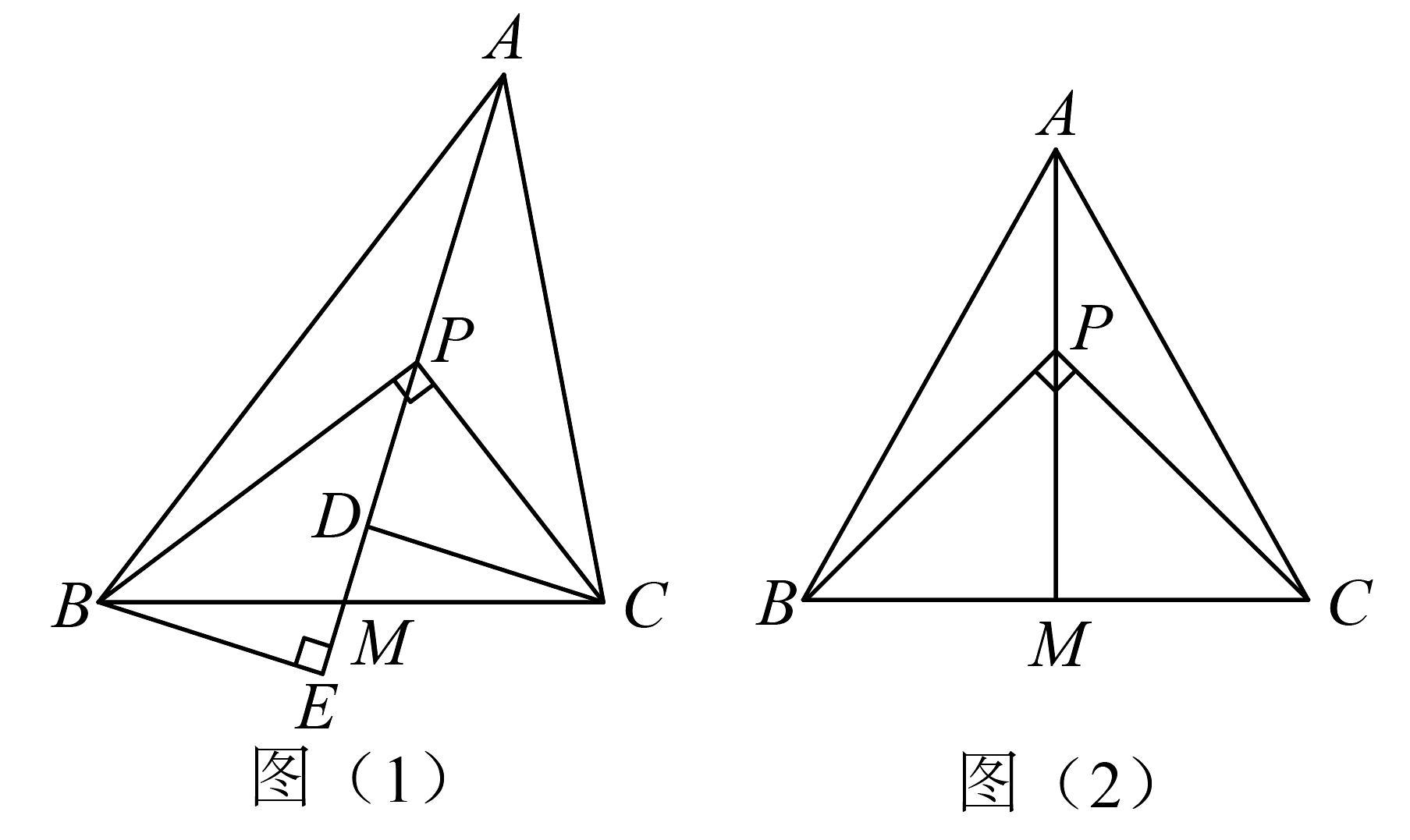 (1)、如图(1),过、分别作中线的垂线,垂足为、 . 求证: .(2)、①如图(2),当 , 且时, (填一个恰当的数).
(1)、如图(1),过、分别作中线的垂线,垂足为、 . 求证: .(2)、①如图(2),当 , 且时, (填一个恰当的数).②如图(1),当 , 为锐角三角形,且时,①中的结论还成立吗?若成立,请写出证明过程;若不成立,也请说明理由.
31. 在△ABC中,∠ACB=90°,AC=BC , AB=4,点D是射线AB上的一个动点,将线段CD绕点C逆时针旋转90°得到线段CD , 连结BD. (1)、如图1,若动点D在线段AB上运动时,求证:△ACD≌△CBD.(2)、如图2,若动点D在射线AB上运动时,连结AD , DD.
(1)、如图1,若动点D在线段AB上运动时,求证:△ACD≌△CBD.(2)、如图2,若动点D在射线AB上运动时,连结AD , DD.①当△ADD为等腰三角形时,求线段AD的长.
②当线段AD= 时, △CDB与△DDB的面积存在3倍的关系.
32. 在等腰△ABC中,AB=AC , 点D是AC上一动点,点E在BD的延长线上,且AB=AE , AF平分∠CAE交DE于点F , 连结FC . (1)、如图1,求证:∠ABE=∠ACF;(2)、如图2,当∠ABC=60°时,在BE上取点M , 使BM=EF , 连结AM .
(1)、如图1,求证:∠ABE=∠ACF;(2)、如图2,当∠ABC=60°时,在BE上取点M , 使BM=EF , 连结AM .求证:△AFM是等边三角形;
(3)、如图3,当∠ABC=45°时,且AEBC时,求证:BD=2EF .33. 在△ABC中,AB=AC , ∠BAC=140°. (1)、如图1,D为BC边上一定点(不与点B , C重合),将△ABD沿AD翻折至△AB'D , 连结B'C , 求∠BAD与∠DCB'的数量关系.(2)、如图2,当点D在BC边上运动时,仍将△ABD沿AD翻折至△AB'D , 连结B'C .
(1)、如图1,D为BC边上一定点(不与点B , C重合),将△ABD沿AD翻折至△AB'D , 连结B'C , 求∠BAD与∠DCB'的数量关系.(2)、如图2,当点D在BC边上运动时,仍将△ABD沿AD翻折至△AB'D , 连结B'C .①当AB'⊥BC时,求∠AB'C的度数.
②当△DB'C为等腰三角形时,求∠BAD的度数.
34. 如图 , 在中,为锐角,点为射线上一点,连接 , 以为一边且在的右侧作正方形 . (1)、如果 , .
(1)、如果 , .①如图 , 当点在线段上时与点不重合 , 线段、所在直线的位置关系为 , 线段、的数量关系为 ;
②如图 , 当点在线段的延长线上时,中的结论是否仍然成立,并说明理由;
(2)、如果 , 是锐角,点在线段上,当 时,点、不重合请直接写出答案,如若需要,自行绘图35. 等边中,点分别在边上,连结 , 以点为中心将逆时针旋转得到 , 连结 , 设 . (1)、当时,如图1,点在上.求证:;(2)、当时,如图2,连接 , 请求出的度数;(3)、当时,如图3,连接 , 当取得最小值时,_____.36. 如图1,△ABC和△CDE均为等腰三角形,AC=BC , CD=CE , AC>CD , ∠ACB=∠DCE=α,且点A、D、E在同一直线上,连接BE .
(1)、当时,如图1,点在上.求证:;(2)、当时,如图2,连接 , 请求出的度数;(3)、当时,如图3,连接 , 当取得最小值时,_____.36. 如图1,△ABC和△CDE均为等腰三角形,AC=BC , CD=CE , AC>CD , ∠ACB=∠DCE=α,且点A、D、E在同一直线上,连接BE . (1)、求证:AD=BE .(2)、如图2,若α=90°,CM⊥AE于M . 若CM=7,BE=10,试求AB的长.(3)、如图3,若α=120°,CM⊥AE于M , BN⊥AE于N , , CM=b , 直接写出AE的值(用a , b的代数式表示).37. 如图,在中,E 是中点,F 是上一动点,连接 , 将沿直线折叠得 .
(1)、求证:AD=BE .(2)、如图2,若α=90°,CM⊥AE于M . 若CM=7,BE=10,试求AB的长.(3)、如图3,若α=120°,CM⊥AE于M , BN⊥AE于N , , CM=b , 直接写出AE的值(用a , b的代数式表示).37. 如图,在中,E 是中点,F 是上一动点,连接 , 将沿直线折叠得 . (1)、如图①,若点D 恰好落在线段上,求证:;(2)、如图②,若为等边三角形,且边长为 , 当点D 落在线段上时,求的长度:(3)、如图③,若为直角三角形, , . 连接 , 若与面积相等,且 , 求的面积.
(1)、如图①,若点D 恰好落在线段上,求证:;(2)、如图②,若为等边三角形,且边长为 , 当点D 落在线段上时,求的长度:(3)、如图③,若为直角三角形, , . 连接 , 若与面积相等,且 , 求的面积.四、实践探究题
-
38.
【问题情境】在数学课上,老师出示了这样一个问题:已知,如图1,中,若 , , 点D为边中点,求边上的中线的取值范围.
经过小组合作交流,找到了解决方法:“倍长中线法”.

 (1)请按照上面的思维框图,完成证明.
(1)请按照上面的思维框图,完成证明.【探究应用】
(2)已知:如图2,中,是边上的中线,E在边上,连接交于F,且 . 求证:;【拓展延伸】
(3)如图3,若 , , , 是边上的中线,E是上一点,连接交于点F,且 , 求的长.39. 综合实践在学习全等三角形的知识时,数学兴趣小组发现这样一个模型:它是由两个共顶角顶点且顶角相等的等腰三角形构成的,在两个等腰三角形位置变化的过程中,始终存在一对全等三角形.数学兴趣小组称此图形为“手拉手模型”.请你和数学兴趣小组的同学一起研究下面的问题.

【探究发现】
(1)如图1,在和中, , , , 点在上,连接、 , 且、、三点共线,则图中与线段相等的线段是 , .
【初步运用】
(2)如图2,在和中, , , , 连接、交于点 . 找出图中与相等的线段,并证明;
【迁移应用】
(3)如图3,在四边形中,点是四边形内一点,且 , , , 请计算的值.
40. 【方法探索】(1)如图 , 已知平分 , 点分别在边上, , . 小明为了证明 , 用了如下两种方法:

构图方法
小明得到下列结论
你认为正确的结论是(写序号)
如图 , 在上取点 , 使 , 连接 .
①;
②;
③ .
Ⅰ.______
如图 , 过点分别作边的垂线,垂足分别记为
①平分;
②;
③ .
Ⅱ.______
【类比探究】
(2)如图 , 已知 , 平分 .
①当点分别在边上时,请你证明: .
②当点分别在所在的直线上, , 且 , 时,请你画出图形并求出的长.
