《三角形的综合》精选压轴题（一）—2025年浙江省八（上）数学期中复习

试卷更新日期：2025-10-19 类型：复习试卷

进入出卷网下载

一、单选题

1. 如图，在△ABC 和△ABD 中，AB=AC=AD，AC⊥AD，AE⊥BC 于点 E，AE 的反向延长线与 BD 交于点 F，连结 CD，则线段 BF，DF，CD 三者之间的关系为（）

A、 $B F - D F = C D$ B、 $B F + D F = C D$ C、 $B F^{2} + D F^{2} = C D^{2}$ D、 $2 B F - 2 D F = C D$

查看试题解析
2. 如图，在四边形ABCD中，AB＝AD＝12，BC＝DC，∠A＝60°，点E在AD上，连接BD，CE相交于点F，CE∥AB．若CE＝9，则CF的长为（）

A、4.5 B、5.5 C、6 D、43

查看试题解析
3. 如图， $∠ C O D = 3 0^{°}$ ，点 $A_{1} ， A_{2} ， A_{3}$ 均在射线 O C 上，点 $B_{1} ， B_{2} ， B_{3} ⋯$ 均在射线 O D 上， $△ A_{1} B_{1} A_{2}$ ， $△ A_{2} B_{2} A_{3} ， △ A_{3} B_{3} A_{4} ⋯$ 均为等边三角形. 若 $O A_{1} = 2$ ，则 $△ A_{n} B_{n} A_{n + 1}$ 的边长为（）

A、2 n B、 $2^{n - 1}$ C、 $2^{n}$ D、 $2^{n + 1}$

查看试题解析
4. 如图， A， B， C， D 四个点顺次在直线 $l$ 上， $A C = a, B D = b$ . 以 A C 为底向下作等腰直角三角形ACE，以 BD 为底向上作等腰三角形 BDF，且 $F B = F D = \frac{5}{6} B D$ ，连结 A F， DE，当 BC 的长度变化时， $△ A B F$ 与 $△ C D E$ 的面积之差保持不变，则 $a$ 与 $b$ 需满足（）

A、 $a = \frac{4}{3} b$ B、 $a = \frac{6}{5} b$ C、 $a = \frac{5}{3} b$ D、 $a = \sqrt{2} b$

查看试题解析
5. 如图，在△ABC中，AC＝1，AC边上的中线 $B D ＝ \sqrt{2}$ 。过点A作AE⊥BC于点E，记BE长为x，BC长为y。当x，y的值发生变化时，下列代数式的值不变的是（）

A、x+y B、x-y C、xy D、x²+y²

查看试题解析
6. 如图，在 $△ A B C$ 中， $A C = B C, ∠ B = 3 0^{°}, D$ 为AB的中点， $P$ 为CD上一点， $E$ 为BC延长线上一点，且 $P A = P E$ .有下列结论：① $∠ C A D = 3 0^{°}$ ；② $∠ P A D + ∠ P E C = 3 0^{°}$ ；③ $△ P A E$ 为等边三角形；④ $C E = C P + 2 P D$ .其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 将两个等边三角形△AGF和△DEF按如图方式放置在等边三角形ABC内．若求四边形ABEF和三角形DGF的周长差，则只需知道( 　)

A、线段AD的长 B、线段EF的长 C、线段FH的长 D、线段DG的长

查看试题解析
8. 如图，在Rt $△ A C B$ 中， $∠ A C B = 9 0^{°}$ ，按下列步骤作图：①分别以点B，C为圆心，大于 $\frac{1}{2} B C$ 的长为半径画弧，两弧相交于点M，.N，作直线MN交AB于点 $D$ ；②以 $C$ 为圆心，CD长为半径画弧交AB于点 $E$ .下方探究得到以下两个结论：① $△ B C E$ 是等腰 $△$ ；②若 $A C = 6, B C = 8$ ，则点 $E$ 到AC的距离为 $\frac{44}{25}$ ，则（）

A、结论①正确，结论②正确 B、结论①正确，结论②错误 C、结论①错误，结论②正确 D、结论①错误，结论②错误

查看试题解析
9. 如图，两块大小不同的等腰直角三角板的直角顶点C重合，连接AD，BE，当点B，D，E在同一条直线上时，则下列结论：①AD＝BE；②BD⊥AD；③BD平分∠ABC；④S_△_ABD＝S_△_ABC﹣S_△_DCE_，其中正确的是（）

A、①② B、①④ C、①③④ D、①②④

查看试题解析
10. 如图，在△ABC中，AB＝AC＝5，BC＝6，D，E分别为线段AB，AC
上一点，且AD＝AE，连接BE、CD交于点G，延长AG交BC于点F．以下四个结论正确的是（）
①BF＝CF； ②若BE⊥AC，则CF＝DF；
③连结EF，若BE⊥AC，则∠DFE＝2∠ABE
④.若BE平分∠ABC，则FG= $\frac{3}{2}$ ；

A、①②③ B、③④ C、①②④ D、①②③④

查看试题解析

二、填空题

11. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $∠ C A B = 30 °$ ， $B C = 2$ ，以 $A B$ 为边作一个等边三角形 $A B D$ ，将 $△ A B D$ 折叠， $H K$ 为折痕．若使点D与点C重合，则 $B K$ 的长度为．

查看试题解析
12. 圆规是尺规作图必不可少的工具之一，图1是我们生活中常见的一种圆规样式．图2是根据圆规结构构造的特殊“圆规”图形．当“圆规”合拢时，点A和点E重合，点C落在线段AB上，AB＝10，∠BAF＝15°．当“圆规”展开一定角度，直立在纸面上时，∠BCD和∠CDF的度数固定不变，EF⊥AE（如图3），则此时以点A为圆心，AE长为半径所作圆的面积为．
（结果保留根号和 π ）

查看试题解析
13. 如图，在△ABC中，AB＝AC ， ∠BAC＝130°，点D在BC边上，△ABD、△AFD关于AD所在的直线对称，∠FAC的角平分线交BC边于点G ，连接FG ． △DFG为等腰三角形时，∠BAD=。

查看试题解析
14. 如图，以Rt△ABC的各边为斜边分别向外作等腰直角三角形，已知点E在线段DF上
BC=1，AC=2，记△AEF面积为S₁ ， △BDE面积为S₂ ，则S₁+S₂的值为

查看试题解析
15. 如图：在等腰直角三角形中，∠BAC＝90°，等边三角形ADE的顶点D在BC边上，连结CE，已知∠DCE＝90°，CD= $\sqrt{2}$ ，则AB的长为，

查看试题解析
16. 如图，在 $△ A B C$ 中，AD是BC边上的高线，CE是AB边上的中线， $D G ⊥ C E$ 于点 $G$ ，且 $E G =$ GC.若 $∠ B E C = 12 6^{°}$ ，则 $∠ B$ 的度数是.

查看试题解析
17. 如图，Rt△ABC中，∠ACB＝90°，∠ABC＝30°，AC＝4，D是线段AB上一个动点，以BD为边在△ABC外作等边△BDE，若F是DE的中点，连结AF，当CF取最小值时， △ACF的周长为。

查看试题解析
18. 如图，在 $△ A B C$ 中， $D$ 是AC边上一点，且 $A B = A D = D C = \sqrt{29}$ ，连结BD并延长至点 $E$ ，使 $\frac{D E}{B D} = \frac{3}{4}$ ，连结AE，若 $∠ E = 4 5^{°}$ ，则 $D E =$ ， $B C =$ .

查看试题解析
19. 如图，在△ABC中，∠BAC=90°，∠B=30°，AB=6，D为AB上一点，且△ADE为等边三角形，AD=2．点F是边BC上的一个动点，连结DF，以DF为边在左侧作一个等边△DFG，连结AG．

(1)、当∠BDF=60°时，DF的长是；

(2)、在整个运动过程中，AG的最小值是．

查看试题解析
20. 如图，A，B，C，D四个点顺次在直线l上，AC=a，BD=b.以AC为底边向下作等腰直角三角形ACE，以BD为底边向上作等腰三角形BDF，且FB=FD= $\frac{5}{6}$ BD.
当a= $\sqrt{18}$ ， b=6时，△AEC和△BFD的面积和是.
连结AF，DE，当BC的长度变化时，若ABF与CDE的面积之差保持不变，则a与b需满足的条件是.

查看试题解析

三、综合题

21. 在一个三角形中，如果一个角是另一个角的2倍，这样的三角形我们称之为“智慧三角形”.比如：三个内角分别为100°，50°，30°的三角形是“智慧三角形”，如图∠MON=40°，在射线OM上找一点A，过点A作AB⊥OM交ON于点B，以A为端点作射线AD，交线段OB于点C.

(1)、∠ABO=

(2)、若∠ACB=60°.求证： △AOC为“智慧三角形”

(3)、当△ABC为“智慧三角形”时，请求出∠OAC的度数

查看试题解析
22. 如图，在△ABC中，AC＝3cm，BC＝4cm，∠ACB＝90°.点D从B点出发沿BA方向移动，移动速度为1cm/s，设移动时间为 t s.

(1)、当CD⊥AB时，求AD ， CD的长度.

(2)、当△ACD是以AD为腰的等腰三角形时，求t的值.

(3)、设点A关于直线CD的对称点为P.当点P落在直线BC上时，连结DP ，求△PDB的面积.

查看试题解析
23. 已知AD为等边△ABC的角平分线，△ABC的边长为6，动点E在直线AD上（不与点A重合），连接BE.以BE为一边在BE的下方作等边△BEF，连接CF.

(1)、如图1，若点E在线段AD上，
①求证：△ABE≌△CBF；
②当DE=2AE，S_△_ABC=9 $\sqrt{3}$ 时，则点F到BC的距离是；

(2)、如图2，若点E在AD的反向延长线上，且直线AE，CF交于点M.
①求∠AMC的度数；
②若P，Q为直线CF上的两个动点，且PQ＝8，连接BP，BQ，判断△BPQ的面积是否为定值.若是，请直接写出这个定值；若不是，请说明理由.

查看试题解析
24. 如图1，在Rt△ABC中，∠ACB＝90°，BC＝4，点D在AB边上运动，△CDB沿着CD折叠得到△CDB^' ，直线CB^'与直线AB相交于E点。

(1)、如图2，若AC＝3，CB^'⊥AB，求CE的长度；

(2)、当△AB^'C为等腰直角三角形时，求AC的值；

(3)、若AC＝3，△EDB^'为钝角三角形，直接写出BD长度的取值范围。

查看试题解析
25. 如图， △ABC是等边三角形，点D沿ABC的边从点A运动到点B，再从点B运动到点C点E是边BC上一点，运动过程中始终满足BD=CE.

(1)、如图1，当点D在AB边上时，连接AE，CD相交于点G①求证：AE=CD.②求∠CGE的度数.

(2)、如图2，当点D在BC边上时，延长AB至点F，使BF=BE，连接AE.DF.判断AE与DF是否相等?并说明理由.

查看试题解析
26. 如图，在 $Δ A B C$ 中， $A B = A C$ ， $∠ B A C = 120 °$ ，延长 $B A$ 至点D，使 $A D = \frac{1}{2} A B$ ，连结 $C D$ ，作 $∠ B A C$ 的平分线与 $∠ B D C$ 的平分线交于点E，连结 $E B$ ， $E C$ ．

(1)、求证： $A D ⊥ C D$ ；

(2)、求 $∠ D B E$ 的度数；

(3)、求 $\frac{B E}{C D}$ 的值．

查看试题解析

四、阅读理解

27. 阅读材料：如图1，汽车M从B镇匀速行驶至A镇时，汽车N恰好从A镇匀速行驶至C镇，汽车M与N的速度比为3：4，通过推理计算可以得出AB：AC=3：4.
抽象应用：如图2，在四边形ABCD中， $A C ⊥ B D, E$ 为垂足， $∠ 1 = ∠ 2$ .当点 $P$ 从点 $A$ 匀速运动到点 $C$ 时，点 $Q$ 恰好从点 $B$ 匀速运动到点 $A . A P = \frac{6}{5} B Q, B E = 8$ ，当点 $P$ 与点 $E$ 重合时， $Q$ 恰好为AB中点

(1)、求AC的长

(2)、连结PQ，当点P与点E重合时，判断PQ与CD的位置关系，并说明理由

(3)、连结DP，当△ADP是以AP为腰的等腰三角形时，求BQ的长

查看试题解析

五、实践探究题

28. 在△ABC中，AB＝AC ， ∠BAC=α，D是直线BC上一点（不与点B ， C重合），以AD为边在AD的右侧作△ADE ，使AD＝AE ， ∠DAE＝∠BAC ，连接CE ．

(1)、【发现】如图1，点D在线段BC上．
①求证：△ABD≌△ACE；
②当∠BAC＝100°时，求∠BCE的度数；

(2)、【探究】在点D的运动过程中，当DE垂直于△ABC的某边所在直线时，求∠DEC的度数．（用含α的式子表示）

查看试题解析
29. 如图
[感知]：如图1，AD平分∠BAC，∠B+∠C=180°且∠B=90°。求证：DB=DC.
[探究]：如图2，AD平分 $∠ B A C, ∠ A B D + ∠ A C D = 18 0^{°}, ∠ A B D ∠ 9 0^{°}$ ，求证： $D B = D C$ .
[应用]：如图3，四边形ABDC中， $∠ B = 4 5^{°}, ∠ C = 13 5^{°}, D B = D C = \sqrt{2}$ ，求 $A B - A C$ 的值。

查看试题解析
30. 【发现问题】小强在一次学习过程中遇到了下面的问题：如图①，AD是△ABC的中线，若AB＝5，AC＝3，求AD的取值范围．
【探究方法】小强所在的小组通过探究发现，延长AD至点E，使ED＝AD．连接BE，可以证出△ADC≌△EDB，利用全等三角形的性质可将已知的边长与AD转化到到△ABE中，进而求出AD的取值范围．

方法小结：从上面的思路可以看出，解决问题的关键是将中线AD延长一倍，构造出全等三角形，我们把这种方法叫做“倍长中线法”．

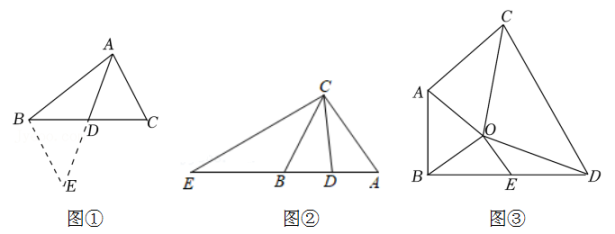(1)、请你利用上面解答问题的思路方法，写出求AD的取值范围的过程；

(2)、【问题解决】
如图②，CB是△AEC的中线，CD是△ABC的中线，且AB＝AC，下列四个选项中：

A．∠ACD＝∠BCD B．CE＝2CD C．∠BCD＝∠BCE D．CD＝CB

直接写出所有正确选项的序号是．

(3)、【问题拓展】
如图③，在△ABO和△CDO中，OA＝OB，OC＝OD，∠AOB与∠COD互补，连接AC、BD，E是BD的中点，求证：OE＝ $\frac{1}{2}$ AC．

查看试题解析