《勾股定理与直角三角形》精选压轴题—2025年浙江省八(上)数学期中复习
试卷更新日期:2025-10-19 类型:复习试卷
一、单选题
-
1. 如图,在中, , , 是的角平分线,E,F分别在 , 边上. , , 连结 , . 若 , 则的面积是( )
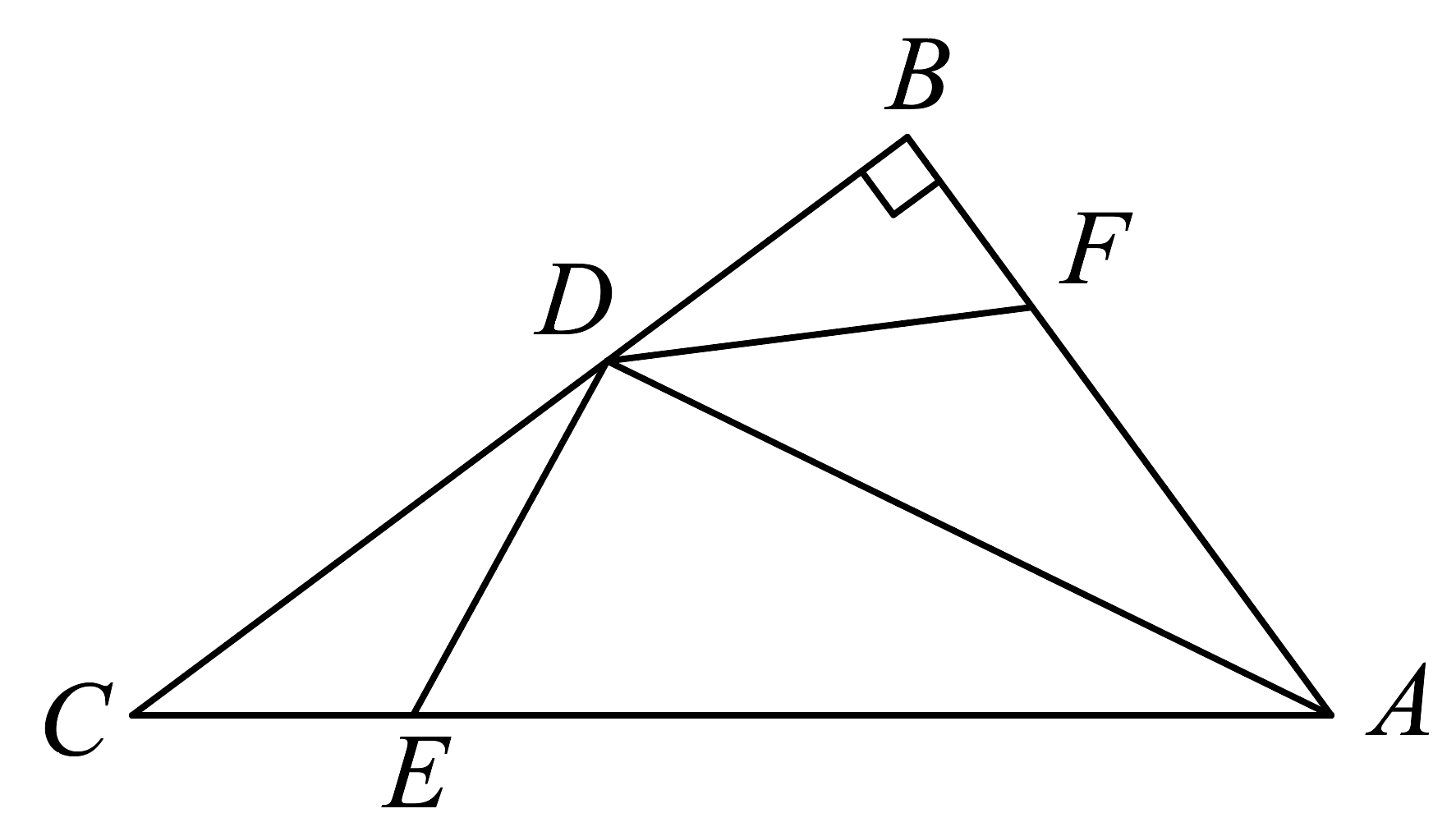 A、 B、24 C、30 D、2. 如图,在中, , , 平分 , 于D,与相交于F,则的长是( )
A、 B、24 C、30 D、2. 如图,在中, , , 平分 , 于D,与相交于F,则的长是( ) A、1 B、 C、 D、23. 如图,在中,分别是的中点,于点 , 连接 . 若的周长是11,则的长为( )
A、1 B、 C、 D、23. 如图,在中,分别是的中点,于点 , 连接 . 若的周长是11,则的长为( ) A、 B、 C、 D、84. 如图,△ABC中, , 以其三边分别向外侧作正方形,然后将整个图形放置于如图所示的长方形中,若要求图中两个阴影部分面积之和,则只需知道( )
A、 B、 C、 D、84. 如图,△ABC中, , 以其三边分别向外侧作正方形,然后将整个图形放置于如图所示的长方形中,若要求图中两个阴影部分面积之和,则只需知道( ) A、以BC为边的正方形面积 B、以AC为边的正方形面积 C、以AB为边的正方形面积 D、△ABC的面积5. 如图, Rt 中, , 分别以 A B, AC, DC为边在AB的同侧作正三角形 ABD 、 ACE 、 BC F, 图中四块阴影部分的面积分別为 , 则
A、以BC为边的正方形面积 B、以AC为边的正方形面积 C、以AB为边的正方形面积 D、△ABC的面积5. 如图, Rt 中, , 分别以 A B, AC, DC为边在AB的同侧作正三角形 ABD 、 ACE 、 BC F, 图中四块阴影部分的面积分別为 , 则 A、 B、 C、 D、6. 欧几里得《几何原本》中给出一种证明勾股定理的方法.如图,在中, , 四边形、四边形、四边形和四边形都是正方形.若的面积为3,正方形的面积为13,则正方形的面积为( )
A、 B、 C、 D、6. 欧几里得《几何原本》中给出一种证明勾股定理的方法.如图,在中, , 四边形、四边形、四边形和四边形都是正方形.若的面积为3,正方形的面积为13,则正方形的面积为( ) A、16 B、19 C、25 D、377. 在图1所示的的网格内有一个八边形,其中每个小方格的边长均为1.经探究发现,此八边形可按图2的方式分割成四个完全一样的五边形和一个小正方形①.现将分割后的四个五边形重新拼接(即图2中的阴影部分),得到一个大正方形 , 发现该正方形中间的空白部分②也是个正方形,记正方形①的面积为1,则大正方形的边长为( )
A、16 B、19 C、25 D、377. 在图1所示的的网格内有一个八边形,其中每个小方格的边长均为1.经探究发现,此八边形可按图2的方式分割成四个完全一样的五边形和一个小正方形①.现将分割后的四个五边形重新拼接(即图2中的阴影部分),得到一个大正方形 , 发现该正方形中间的空白部分②也是个正方形,记正方形①的面积为1,则大正方形的边长为( ) A、3 B、 C、 D、8. 如图,中, , 分别以为边在AB的同侧作正三角形 , 图中四块阴影部分的面积分别为 , , , , 则( )
A、3 B、 C、 D、8. 如图,中, , 分别以为边在AB的同侧作正三角形 , 图中四块阴影部分的面积分别为 , , , , 则( )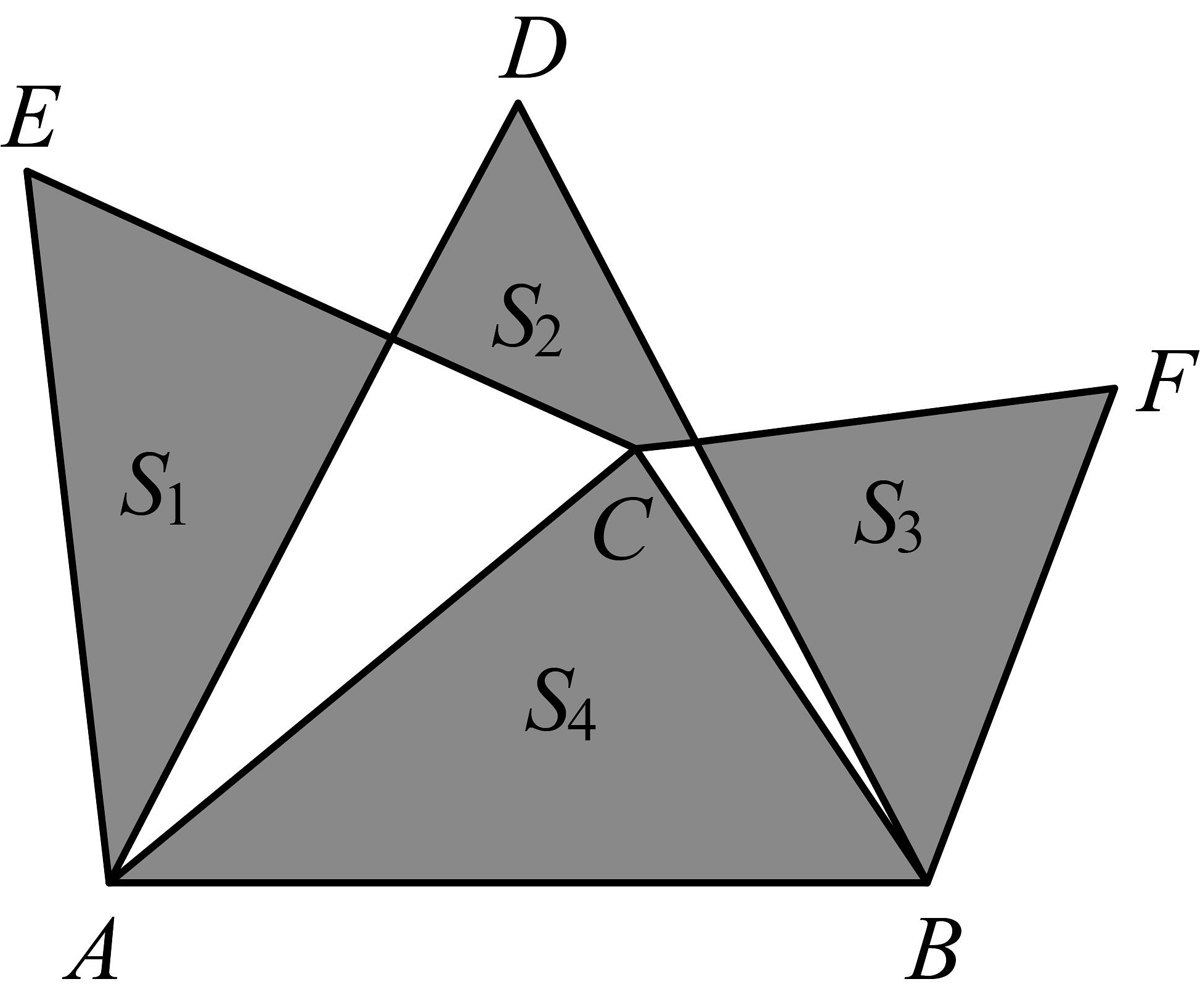 A、 B、 C、 D、9. 如图,在Rt△ABC中,∠ACB90°, 分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN , 若把图中阴影部分面积分别记为S1、S2、S3、S4并把它们的面积之和记为L , 则L与Rt△ABC的面积S存在何种数量关系?( )
A、 B、 C、 D、9. 如图,在Rt△ABC中,∠ACB90°, 分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN , 若把图中阴影部分面积分别记为S1、S2、S3、S4并把它们的面积之和记为L , 则L与Rt△ABC的面积S存在何种数量关系?( ) A、L=2S B、L=3S C、L=4S D、L=5S10. 如图,在中, , 以的各边为边作三个正方形,点落在GF上,若正方形AEDB的面积是14, , 则阴影部分的面积为( )
A、L=2S B、L=3S C、L=4S D、L=5S10. 如图,在中, , 以的各边为边作三个正方形,点落在GF上,若正方形AEDB的面积是14, , 则阴影部分的面积为( ) A、7 B、7.5 C、8 D、8.511. 如图,四个全等的直角三角形与中间的小正方形EFGH拼成了一个大正方形ABCD , 连结AC , 交BE于点 , 若正方形ABCD的面积为.则的值是( )
A、7 B、7.5 C、8 D、8.511. 如图,四个全等的直角三角形与中间的小正方形EFGH拼成了一个大正方形ABCD , 连结AC , 交BE于点 , 若正方形ABCD的面积为.则的值是( ) A、5.5 B、6.5 C、7 D、7.512. 如图,清代数学家李锐在其著作《勾股算术细草》中利用三个正方形出入相补的方法证明了勾股定理.如图,在中, , 分别以和为边,按如图所示的方式作正方形、和 , 与交于点 , 与交于点 . 若四边形和的面积和为5,四边形和的面积和为12,则的值为( )
A、5.5 B、6.5 C、7 D、7.512. 如图,清代数学家李锐在其著作《勾股算术细草》中利用三个正方形出入相补的方法证明了勾股定理.如图,在中, , 分别以和为边,按如图所示的方式作正方形、和 , 与交于点 , 与交于点 . 若四边形和的面积和为5,四边形和的面积和为12,则的值为( ) A、 B、 C、 D、13. 如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两个正方形按图2的方式放置在大正方形内,若四边形面积为6,四边形的面积为2,四边形的面积为2.5,四边形的面积为4,则知道图中阴影部分的面积是( )
A、 B、 C、 D、13. 如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两个正方形按图2的方式放置在大正方形内,若四边形面积为6,四边形的面积为2,四边形的面积为2.5,四边形的面积为4,则知道图中阴影部分的面积是( ) A、1.5 B、2 C、2.5 D、3
A、1.5 B、2 C、2.5 D、3二、填空题
-
14. 如图,在长方形纸片中, , , 点M 为上一点,将沿翻至 , 交于点G,交于点F,且 , 则的长度是
 15. 第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”.它由4个全等的直角三角形拼合而成,若图中大、小正方形的面积分别为13和1、则直角三角形的较长直角边长为 .
15. 第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”.它由4个全等的直角三角形拼合而成,若图中大、小正方形的面积分别为13和1、则直角三角形的较长直角边长为 . 16. 如图是2002年北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,若图中大小正方形的面积分别为13和1,且直角三角形的两直角边分别为a,b,则的值为 .
16. 如图是2002年北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,若图中大小正方形的面积分别为13和1,且直角三角形的两直角边分别为a,b,则的值为 . 17. 青朱出入图(图1)是东汉末年数学家刘徽根据“割补术”运用数形关系证明勾股定理引入的图形,该图中的两个青入的三角形分别与两个青出的三角形全等,朱入与朱出的三角形全等,朱方与青方是两个正方形.为便于叙述,将其绘成图2,若记朱方对应正方形的边长为a,青方对应正方形的边长为b,已知 , , 则图2中的阴影部分面积为 .
17. 青朱出入图(图1)是东汉末年数学家刘徽根据“割补术”运用数形关系证明勾股定理引入的图形,该图中的两个青入的三角形分别与两个青出的三角形全等,朱入与朱出的三角形全等,朱方与青方是两个正方形.为便于叙述,将其绘成图2,若记朱方对应正方形的边长为a,青方对应正方形的边长为b,已知 , , 则图2中的阴影部分面积为 . 18. 将一块三角形纸板剪成如图1所示的①②③三块,再拼成不重叠、无缝隙的正方形(如图2).若的面积为9, , 则的长为 .
18. 将一块三角形纸板剪成如图1所示的①②③三块,再拼成不重叠、无缝隙的正方形(如图2).若的面积为9, , 则的长为 . 19. 如图, 在 中, , 点D, E 分別在 A C, B C 上, 且 , 将 沿DE 折叠,点C恰好落在AB边上的点F处, CF 与DE交于点G.下列结论:其中正确的结论有。(填序号)
19. 如图, 在 中, , 点D, E 分別在 A C, B C 上, 且 , 将 沿DE 折叠,点C恰好落在AB边上的点F处, CF 与DE交于点G.下列结论:其中正确的结论有。(填序号)①AB=2CF.
②若 , 则 ;
③若CD=1.5, CE=2, 则DG·GE=1.2;
④若AC=4, BC=3, 则CG=1.25.
 20. 如图,在矩形中,点E在边上,沿折叠得到 , 且点B,F,E三点共线,连接 , 若 , , 则 , .
20. 如图,在矩形中,点E在边上,沿折叠得到 , 且点B,F,E三点共线,连接 , 若 , , 则 , . 21. 如图,在矩形中, , , 将矩形折叠,使点与点重合,点落在点处,折痕为 , 则 , .
21. 如图,在矩形中, , , 将矩形折叠,使点与点重合,点落在点处,折痕为 , 则 , . 22. 沿海地区台风频发,为了安全的需要,人们常常会在窗户上加装铰链,如下图所示,安装方式有水平安装(如图1,2)和上悬安装(如图3,4)两种形式.悬挂臂DE安装在窗户上,交点A处装有滑块,滑块可以左右滑动,支点B、C、D安装在一根钢筋上,其中AC//ED , AC=20cm , CD=10cm , BD=40cm , 我们把DE所在的直线与直线AB所成的夹角称作窗户打开角.当水平安装的窗户打开角为90°时,AB=cm . 当上悬安装的窗户打开角为30°时,AB=cm .
22. 沿海地区台风频发,为了安全的需要,人们常常会在窗户上加装铰链,如下图所示,安装方式有水平安装(如图1,2)和上悬安装(如图3,4)两种形式.悬挂臂DE安装在窗户上,交点A处装有滑块,滑块可以左右滑动,支点B、C、D安装在一根钢筋上,其中AC//ED , AC=20cm , CD=10cm , BD=40cm , 我们把DE所在的直线与直线AB所成的夹角称作窗户打开角.当水平安装的窗户打开角为90°时,AB=cm . 当上悬安装的窗户打开角为30°时,AB=cm .