【北京卷】备战2026年中考数学真题变式阶梯训练第27~28题-在线组卷题库

1. 在△ABC中，∠ACB =90°，∠ABC=α，点 D 在射线 BC上，连接AD，将线段AD绕点A 逆时针旋转 180°-2α得到线段AE (点E 不在直线AB上)，过点E作EF∥AB $，$ 交直线 BC 于点 F.

(1)、如图1，α=45°，点 D 与点C 重合，求证： BF =AC；

(2)、如图2，点D，F都在 BC的延长线上，用等式表示 DF 与BC的数量关系，并证明.

查看试题解析

2. 如图，在 $△ A B C$ 中， $A B = A C$ ， D是BC的中点，过点 $A$ 作 $A E / / B C$ ，使 $A E = B D$ ，连接BE.求证：四边形 $A E B D$ 是矩形.

查看试题解析
3. 如图，在 $△ A B C$ 中，点E，F分别为边AB，AC的中点，延长EF到点G使 $F G = E F$ .
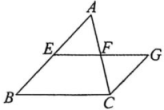
求证：四边形EGCB是平行四边形.

查看试题解析
4. 如图，在四边形ABCD中，E是BC延长线上的一点，AD＝BC， $∠ D = ∠ D C E$ ．求证：四边形ABCD是平行四边形．

查看试题解析

5. 如图，在Rt△ABC中，∠ABC=90°，∠ACB=30°，将△ABC 绕点C 顺时针旋转一定的角度α得到△DEC，点A，B的对应点分别是点D，E.

(1)、如图1，当点 E恰好在AC 边上时，连接AD，求∠ADE的度数；

(2)、如图2，点 F 是AC上一点，当旋转角α=60°且∠FBC=30°时，连接EB，DF，请判断四边形 BFDE 的形状，并说明理由.

查看试题解析
6. 如图，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = 60 °$ ，将 $△ A B C$ 绕点C顺时针旋转 $a °$ 得到 $△ D E C$ ，点D恰好落在边 $A B$ 上．

(1)、求a的值；

(2)、点F是边 $D E$ 上一点， $D E = m D F$ ，连接 $C F$ ．当 $m =$ _________时，四边形 $A C F D$ 为平行四边形．

查看试题解析
7. 如图，在 $R t △ A B C$ 中， $∠ A B C = 90 °$ ， $∠ A C B = 30 °$ ，将 $△ A B C$ 绕点C顺时针旋转一定的角度 $α$ 得到 $△ D E C$ ，点A，B的对应点分别是点D，E．

(1)、如图①，当点E恰好在AC边上时，连接AD，求∠ADE的度数；

(2)、如图②，当 $α = 60^{\circ}$ 时，若点F为AC边上的动点，当∠FBC为何值时，四边形BFDE为平行四边形？请说出你的结论并加以证明

查看试题解析

8. 综合与实践
问题情境：
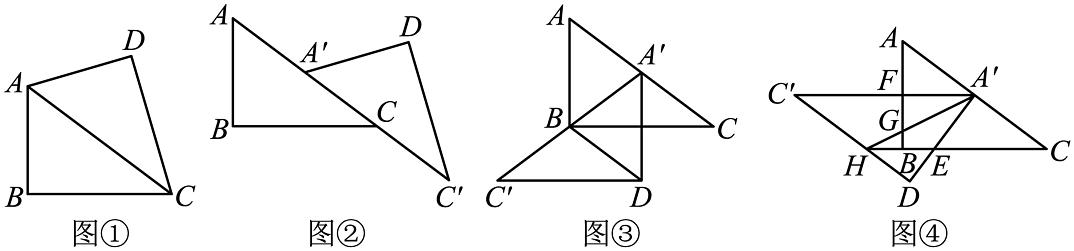
在综合与实践课上，老师让同学们以“三角形的旋转”为主题开展探究活动，如图①，在四边形 $A B C D$ 中． $A D = A B = 3, D C = B C = 4$ ．
$∠ D = ∠ B = 90 °$ ，如图②，保持 $△ A B C$ 不动，将 $△ A D C$ 沿着 $A C$ 方向向下平移，使得点 $A$ 与 $A C$ 边的中点 $A^{'}$ 重合，得到 $△ A^{'} D C^{'}$ ．
操作发现：
（1）连接 $C D$ ，试猜想 $C D$ 和 $C C^{'}$ 的数量关系，并说明理由；
（2）如图③，在图②的基础上，再将 $△ A^{'} D C^{'}$ 以点 $A^{'}$ 为旋转中心，按顺时针方向旋转一定角度，使点 $A^{'}, B, C^{'}$ 在同一条直线上（ $B$ 在 $A^{'}, C^{'}$ 中间），连接 $B D$ ．试判断四边形 $A A^{'} D B$ 的形状，并证明你的结论；
实践探究：
（3）如图④，在图②的基础上，按（2）中的旋转方式继续旋转 $△ A^{'} D C^{'}$ ．当 $A^{'} D$ 第一次恰好与 $A C$ 垂直时停止旋转，设 $A^{'} D$ 与 $B C$ 交于点 $E$ ， $A^{'} C^{'}$ 与 $A B$ 交于点 $F$ ，延长 $C B$ 交 $C^{'} D$ 于点 $H$ ，连接 $A^{'} H$ 交 $A B$ 于点 $G$ ，求线段 $A^{'} H$ 的长．

查看试题解析
9. 在△ABC中，AB＝BC＝2，∠ABC＝120°，将△ABC绕点B顺时针旋转角α（0°＜α＜90°）得△A₁BC₁ ， A₁B交AC于点E，A₁C₁分别交AC、BC于D、F两点.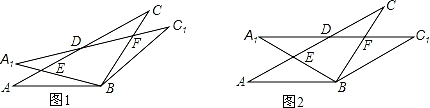

(1)、如图1，观察并猜想，在旋转过程中，线段EA₁与FC有怎样的数量关系？并证明你的结论；

(2)、如图2，当α＝30°时，试判断四边形BC₁DA的形状，并说明理由；

(3)、在（2）的情况下，求ED的长.

查看试题解析

10. 在平面直角坐标系xOy中，对于点A和⊙C 给出如下定义：若⊙C上存在两个不同的点M，N，对于⊙C上任意满足AP=AQ的两个不同的点P，Q，都有 $∠ P A Q \leq ∠ M A N ，$ 则称点A是⊙C的关联点，称∠MAN的大小为点A与⊙C的关联角度.(本定义中的角均指锐角、直角、钝角或平角)

(1)、如图，⊙O 的半径为1.
①在点 $A_{1} (\frac{1}{2}, 0) ， A_{2} (\frac{4}{3}, 0) ， A_{3} (2, 0)$ 中，点是⊙O的关联点且其与⊙O的关联角度小于 $9 0^{\circ} ，$ 该点与⊙O 的关联角度为°；
②点B(1，m)在第一象限，若对于任意长度小于1的线段BD，BD 上所有的点都是⊙O的关联点，则m的最小值为；

(2)、已知点E(1，3)，F(4，3)，T(t，0)，⊙T经过原点，线段EF上所有的点都是⊙T的关联点，记这些点与⊙T的关联角度的最大值为α.若 $9 0^{\circ} \leq α \leq 18 0^{\circ} ，$ 直接写出t的取值范围.

查看试题解析

11. 如图，在平面直角坐标系中，点 $P$ 在第一象限内， $⊙ P$ 与 $x$ 轴相切于点 $C$ ，与 $y$ 轴相交于点 $A (0 ， 8)$ ， $B (0 ， 2)$ ．连接 $A C$ ， $B C$ ．

(1)、求点 $P$ 的坐标；

(2)、求 $c o s ∠ A C B$ 的值．

查看试题解析

12. 在平面直角坐标系 $x O y$ 中， $⊙ O$ 的半径为1，对于线段 $A B$ 和x轴上的点P，给出如下定义：若将线段 $A B$ 绕点P旋转 $180 °$ 可以得到⊙ $O$ 的弦 $A_{1} B_{1}$ （ $A_{1}, B_{1}$ 分别为A，B的对应点），则称线段 $A B$ 为 $⊙ O$ 以P为中心的“相关线段”．

(1)、如图，已知点 $A (- 2, - 1), B (- 2, 0), C (- 2, 1), D (- 1, 1)$ ，在线段 $A C$ ， $B D$ ， $C D$ 中， $⊙ O$ 以P为中心的“相关线段”是________；

(2)、已知点 $E (- 3, 1)$ ，线段 $E F$ 是 $⊙ O$ 以P为中心的“相关线段”，求点F的横坐标 $x_{F}$ 的取值范围．

(3)、已知点 $E (m, 1)$ ，若直线 $y = - \sqrt{3} x + 2 m$ 上存在点F，使得线段 $E F$ 是 $⊙ O$ 以P为中心的“相关线段”，直接写出m的取值范围：___________．

查看试题解析

【北京卷】备战2026年中考数学真题变式阶梯训练第27~28题

一、原题27

二、变式1基础

三、变式2巩固

四、变式3提高

五、原题28

六、变式1（基础）

七、变式2（巩固）

八、变式3（提高）