【青海卷】备战2026年中考数学真题变式阶梯训练第23~25题-在线组卷题库

1. 为了让学生体验青海民俗文化，某学校开设了特色艺术实践课程，课程分别是：A.五谷画，B.彩陶，C.剪纸，D.排灯.现学校要了解学生最感兴趣的课程情况，从全校学生中随机抽取部分学生进行调查(每位学生必选且只能选一个课程)，根据调查结果，绘制了如下两幅不完整的统计图：
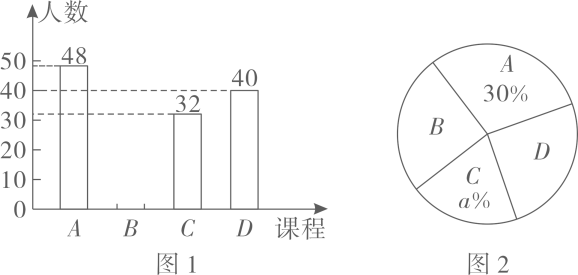
根据以上提供的信息，解答下列问题：

(1)、此次被调查的学生总人数为；扇形统计图中 $a =$ ；

(2)、补全条形统计图；

(3)、该校有1600人，请你估计该校对课程D感兴趣的学生有多少名?

(4)、甲、乙两名同学从A、B、C、D四个课程中任选一个，用树状图或列表法求两人恰好选到同一个课程的概率.

查看试题解析

2. 为进一步弘扬爱国精神，引导青少年听党话，跟党走，发场红色传统，温州道德馆举办了“党的故事我来讲”主题活动，计划开展四项活动：A：党史演讲比赛，B：党史手抄报比赛，C：党史知识竞赛，D：红色歌咏比赛.宣传部对学生最喜欢的一项活动进行调查，随机抽取了部分学生，并将调查结果绘制成图1，图2两幅不完整的统计图.请结合图中信息解答下列问题：

(1)、本次共调查了名学生；图2中 $m =$ ；并将图1的条形统计图补充完整；

(2)、已知在被调查的最喜欢“党史知识竞赛”项目的4个学生中只有1名女生，现从这4名学生中任意抽取2名学生参加该项目比赛，请用画树状图或列表的方法，求出恰好抽到一名男生一名女生的概率.

查看试题解析
3. 某区准备组织部分学校的中小学生到A ， B ， C ， D ， E五个景区“一日游”，每名学生只能在五个景区中任选一个．为估计到各景区旅游的人数，随机抽取这些学校的部分学生，进行了“五个景区，你最想去哪里”的问卷调查，在统计了所有的调查问卷后将结果绘制成如图所示的统计图．

(1)、求参加问卷调查的学生数，并将条形统计图补充完整；

(2)、若参加“一日游”的学生为 $1000$ 人，请估计到A景区旅游的人数．

查看试题解析

4. 粮食安全，事关国计民生，增强学生粮食安全意识，培养学生节粮爱粮的良好生活习惯，已成为学校教育的一个重要共识．为此，某学校开设了相关校本课程，并在期末进行了结业测试．现从中随机抽取了部分学生的结业成绩（满分：100分，所有成绩均不低于75分），整理并绘制了如下尚不完整的统计图表．
组别
成绩/分
额数（人数）
1
75≤x＜80
10
2
80≤x＜85
a
3
85≤x＜90
35
4
90≤x＜95
25
5
95≤x≤100
b
根据以上信息．解答下列问题：

(1)、请直接写出统计表中的a＝，b＝，第4组人数在结业成绩扇形统计图中所对应的圆心角是度；

(2)、请补全上面的结业成绩频数分布直方图；

(3)、现从第5组中选拔演讲能力出众的2名男生和3名女生组成“粮食安全”宣讲团．并从中随机抽取2人进社区宣讲，求所抽取的2人恰好是1名男生和1名女生的概率．

查看试题解析
5. 2025年初，某省共发生电动自行车事故96起，从已调查完毕事故原因看，绝大部分的事故源于电动车不遵守交通规则造成；广大初中生及家长作为电动车的使用群体之一，教会他们规范骑行成为校园安全的重要任务．深圳市某中学制作了时长100分钟的电动车交通安全知识的教育视频并组织学生周末观看，学校随机抽查了部分学生观看视频的时长，并绘制如下不完整的统计图表．
部分学生观看教育视频时长扇形统计图
部分学生观看教育视频时长频数分布表
组别
时长x/分钟
频数
A
0≤x＜20
20
B
20≤x<40
40
C
40≤x＜60
▲
D
60≤x<80
60
E
80≤x≤100
10
结合以上信息，回答下列问题：

(1)、本次调查属于 ▲ 调查，本次调查的样本容量为 ▲ ；

(2)、样本数据的中位数落在 ▲ 组；

(3)、若本校共2000人，观看视频时长低于40分钟即为“不合格”，请估算本校有多少同学的成绩是“不合格”，并根据调查结果对类似自行观看教育视频的活动提出一条合理化建议．

查看试题解析
6. 中国新能源产业强势崛起．中国车企在政策引导和支持下，瞄准纯电、混动和氢燃料等多元技术路线，加大研发投入形成了领先的技术优势，诞生了像比亚迪、小米、小鹏、蔚来和理想等一批优秀的新能源车企.2024年，中国新能源汽车产销量均突破1280万辆，连续10年位居全球第一、在某次汽车展览会上，工作人员随机抽取了部分参展人员进行了“我最喜欢的汽车类型”的调查活动（每人限选其中一种类型），并将数据整理后，绘制成下面有待完成的统计表、条形统计图和扇形统计图．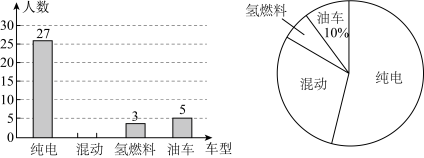
类型
人数
百分比
纯电
$m$
$54 %$
混动
$n$
$a %$
氢燃料
3
$b %$
油车
5
$c %$
请根据以上信息，解答下列问题：

(1)、本次调查活动随机抽取了人；表中 $a =$ ， $b =$ ；

(2)、请补全条形统计图：

(3)、若此次汽车展览会的参展人员共有4000人，请你估计喜欢新能源（纯电、混动、氢燃料）汽车的有多少人．

查看试题解析

7. 雨花区某小区为了解居民对“垃圾分类知识”的掌握情况，从小区班机抽取部分居民进行测试，并对成绩（百分制）进行整理、描述和分析，下面给出部分信息：
①学生成绩的统计图如图（数据分为五组：50≤x<60，60≤x<70，70≤x<80，80≤x<90，90≤x≤100）·
②80≤x<90这一组成绩是 80、80、80、81、81、82、83、84、84、85、85、87、88、89、89、89.
③成绩不低于90分为优秀.
根据以上信息，回答下列问题：

(1)、本次调查采用的方式是（选填“全面调查”或“抽样调查”）；

(2)、补全频数分布直方图；

(3)、求出成绩在60≤x<70这一组所在扇形的圆心角度数：

(4)、若该小区共有400名居民，请估计达到优秀的人数.

查看试题解析
8. 为了解学生零花钱的使用情况，校团委随机调查了本校部分学生每人一周的零花钱数额，并绘制了如图所示的两个统计图（部分未完成）。请根据图中信息，回答下列问题：

(1)、校团委随机调查了 ▲ 名学生，并请你补全条形统计图：

(2)、被调查的部分学生一周零花钱的平均数是元，众数是元.

(3)、“50元”所在扇形的圆心角的度数为.

(4)、为捐助贫困山区希望小学，全校1000名学生每人自发地捐出一周零花钱，请估算全校学生共捐款多少元?

查看试题解析

9. 在平面直角坐标系中，抛物线 $y = a x^{2} + b x - 3 (a \neq 0)$ 与x轴交于A ， B两点，点B的坐标为(1，0)，点 C(2，5)在抛物线上.

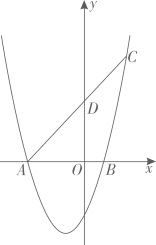(1)、求抛物线的解析式；

(2)、 ①求点A的坐标；
②当y＜0时，根据图象直接写出x的取值范围；

(3)、连接AC交y轴于点D ，在y轴上是否存在点 P ，使 $△ A C P$ 是以AC为直角边的直角三角形，若存在，请直接写出所有符合条件的点P坐标，若不存在，请说明理由.

查看试题解析

10. 已知抛物线 $y = - x^{2} + 2 x + 8$ 与x轴相交于点A，B（点A 在点B 的左侧），与y轴相交于点C.

(1)、求点 B，C 的坐标.

(2)、设点C'与点C 关于该抛物线的对称轴对称.在y 轴上是否存在一点P，使△PCC'与△POB 相似，且 PC 与PO 是对应边? 若存在，求出点P 的坐标；若不存在，请说明理由.

查看试题解析
11. 如图，抛物线 $y = a x^{2} - 2 a x -$ 3与x轴分别交于点A，B(点B在点A的右侧)，与y轴交于点C，连接BC.点D 与点 C关于原点O 对称，作射线BD 交抛物线于点E，且 $B D = D E .$

(1)、求抛物线的表达式；

(2)、过点B作 $B F ⟂ B C$ 交抛物线的对称轴于点 F，以点 C 为圆心，以 $\sqrt{5}$ 的长为半径作⊙C，点T为⊙C上的一个动点，求 $\frac{\sqrt{5}}{5} T B + T F$ 的最小值.

查看试题解析
12. 如图，在平面直角坐标系中，一次函数 $y = - 2 x + 6$ 的图象与 $x$ 轴交于点 $A$ ，与 $y$ 轴交于点 $B$ ，抛物线 $y = - x^{2} + b x + c$ 经过 $A 、 B$ 两点，在第一象限的抛物线上取一点 $D$ ，过点 $D$ 作 $D C ⊥ x$ 轴于点 $C$ ，交 $A B$ 于点 $E$ ．

(1)、求这条抛物线所对应的函数表达式；

(2)、是否存在点 $D$ ，使得 $△ B D E$ 和 $△ A C E$ 相似？若存在，请求出点 $D$ 的坐标，若不存在，请说明理由．

查看试题解析

13. 如图，已知抛物线 $y = \frac{1}{2} x^{2} + b x + c$ 与直线 $y = \frac{1}{2} x + 3$ 相交于A，B两点，交x轴于C，D 两点，连接AC，BC，已知A(0，3)，C(-3，0).

(1)、求此抛物线的解析式.

(2)、在抛物线对称轴l 上找一点M，使|MB-MD|的值最大，并求出这个最大值.

(3)、点 P 为 y 轴右侧抛物线上一动点，连接 PA，过点 P 作PQ⊥PA 交y 轴于点Q，问：是否存在点 P，使得以A，P，Q 为顶点的三角形与△ABC 相似?若存在，请求出符合条件的点 P的坐标；若不存在，请说明理由.

查看试题解析
14. 抛物线L： $y = - x^{2} + b x + c$ 经过点A(0，1)，与它的对称轴直线x=1交于点 B.

(1)、直接写出抛物线 L 的解析式.

(2)、如图①，过定点的直线y= kx-k+4(k<0)与抛物线L 交于点M，N，若△BMN 的面积等于1，求k 的值.

(3)、如图②，将抛物线L 向上平移m(m>0)个单位长度得到抛物线L₁ ，抛物线L₁与y轴交于点C，过点C作y轴的垂线交抛物线L₁于另一点 D. F为抛物线L₁的对称轴与x轴的交点，P为线段OC 上一点.若△PCD 与以P，O，F 为顶点的三角形相似，并且符合条件的点 P 恰有2个，求m 的值及相应点 P 的坐标.

查看试题解析
15. 如图，在平面直角坐标系中，抛物线 $y = - 2 x^{2} + b x + c$ 与 $x$ 轴相交于 $A (1, 0)$ ， $B$ 两点（点 $A$ 在点 $B$ 左侧），顶点为 $M (2, d)$ ，连接 $A M$ ．

(1)、求该抛物线的函数表达式；

(2)、如图1，若 $C$ 是 $y$ 轴正半轴上一点，连接 $A C, C M$ ．当点 $C$ 的坐标为 $(0, \frac{1}{2})$ 时，求证： $∠ A C M = ∠ B A M$ ；

(3)、如图2，连接 $B M$ ，将 $△ A B M$ 沿 $x$ 轴折叠，折叠后点 $M$ 落在第四象限的点 $M^{'}$ 处，过点 $B$ 的直线与线段 $A M^{'}$ 相交于点 $D$ ，与 $y$ 轴负半轴相交于点 $E$ ．当 $\frac{B D}{D E} = \frac{8}{7}$ 时， $3 S_{△ A B D}$ 与 $2 S_{△ M^{'} B D}$ 是否相等？请说明理由．

查看试题解析

16. 如图，矩形 $O A B C$ 的边 $O A ， O C$ 在坐标轴上，顶点B在第一象限，且在直线 $y = \frac{1}{2} x$ 上， $O A = 8$ ，点D从点O开始沿 $O A$ 边向点A以每秒2个单位的速度移动，与此同时，点E从点A开始沿 $O A$ 边向点O以每秒1个单位的速度移动， $D F ⊥ x$ 轴，交 $O B$ 于点F，连接 $E F$ ，当点D到达点A时，两点同时停止移动，设移动时间为t秒．

(1)、直接写出： $A B =$ ______， $D F =$ _______（含t的代数式表示）．

(2)、当点D在点E的左侧时，若 $△ D E F$ 的面积等于2，求t的值．

(3)、在整个过程中，
①若在矩形 $O A B C$ 的边上能找到点P，Q，使得以E，F，P，Q为顶点的四边形为正方形，求出所有满足条件的t的值．
②以 $D A ， D F$ 为邻边作矩形 $D A G F$ ，连接 $E G$ ，取线段 $E G$ 的中点Q，连接 $F Q$ ，求 $F Q$ 的最小值（直接写出答案）．

查看试题解析

17. 活动与探究

解码蜜蜂的“家”——为什么蜂房是正六边形的?

蜜蜂的“集体宿舍”是由多个正六边形密铺在一起的，这些密铺的正六边形使得蜂房之间没有空隙，一点儿也不浪费空间.这是数学中的密铺(或镶嵌)问题.平面图形的密铺(或镶嵌)是指用形状、大小完全相同的一种或多种平面图形进行拼接，使彼此之间不留空隙、不重叠地铺成一片.

(1)、探究一：若只用一种正多边形，哪些正多边形可以密铺?

平面图形	每个内角度数	能否整除	能否密铺
正三角形	60°	360°÷60°=6	能
正方形	①	②	能
正五边形	108°	$360 ° \div 108 ° = \frac{10}{3}$	不能
正六边形	120°	$360 ° \div 120 ° = 3$	能
正七边形	900° 7	$360 ° \div \frac{900 °}{7} = \frac{14}{5}$	不能
正八边形	135°	③	④
…	…	…

请补全上述表格①； ②； ③； ④.

(2)、探究二：在能密铺的正多边形中，哪种形状最省材料?

数学视角：蜜蜂的身体可近似看成圆柱，若圆柱底面半径为1，当蜂房恰好容纳一只蜜蜂即正多边形的内切圆半径均为1时，比较正三角形，正方形和正六边形周长的大小.

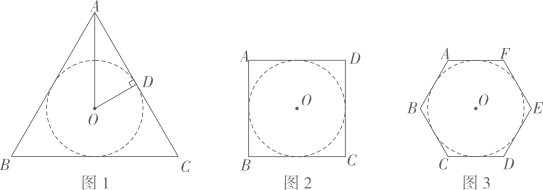
观察图1，发现⊙O是正三角形ABC的内切圆，与AC切于点D ， ( $O D ⟂ A D,$ $∠ O A D = 3 0^{\circ}, O D = 1,$ ，在Rt△ADO中， . $A D = \sqrt{3},$ 则 $△ A B C$ 的周长为( $6 \sqrt{3} .$

①如图2，正方形ABCD的周长为；

②如图3，求出正六边形的周长(写出求解过程).

(3)、探究三：在能密铺的正多边形中，哪种形状可以使蜜蜂的活动空间最大?

数学视角：假设蜜蜂建造蜂房的材料总量即周长一定，比较正三角形、正方形和正六边形面积的大小.

若正多边形的周长都为12，则正三角形的面积为；正方形的面积为；正六边形的面积为.

【得出结论】综上所述：在相同条件下，正六边形结构最省材料，能使蜜蜂的活动空间最大，是建造蜂房的最优方案.

查看试题解析

18. 仅用无刻度直尺按要求画图，不写画法，保留画图痕迹．

(1)、如图， $B C$ 为 $⊙ O$ 的弦，画一条与 $B C$ 长度相等的弦；

(2)、如图，正五边形 $A B C D E$ 内接于圆，请作出一条直径；

查看试题解析
19. 如图正方形 $A B C D$ 内接于 $⊙ O$ ， $E$ 为 $\overset{⌢}{C D}$ 任意一点，连接 $D E$ 、 $A E$ ．

(1)、求 $∠ A E D$ 的度数．

(2)、如图2，过点 $B$ 作 $B F ∥ D E$ 交 $⊙ O$ 于点 $F$ ，连接 $A F$ ， $A F = 1$ ， $A E = 4$ ， $D E < 2.5$ ，求 $D E$ 的长度．

查看试题解析
20. 如图，A，B，C，D，E是⊙O上的5等分点，连结AC，CE，EB，BD，DA，得到一个五角星图形和五边形MNFGH．

(1)、求∠CAD的度数．

(2)、连结AE，求证：AE=ME．

查看试题解析
21. 想一想：用若干个全等的正五边形能镶嵌平面吗？为什么？
事实上，如果用正多边形来镶嵌平面，那么共顶点的各个角之和必须等于 $36 0^{°}$ ．例如，用正六边形镶嵌平面（图5），共顶点的3个角之和为 $3 \times 12 0^{°} = 36 0^{°}$ ．因此能镶嵌平面的正多边形的内角度数一定能整除360，所以，能单独镶嵌平面的正多边形只有3种，即正三角形、正方形、正六边形．
如果用多种正多边镶嵌平面，那么能镶嵌平面的正多边图形就不止上面所说的这3种．

查看试题解析

22. 如图，正三角形ABC、正方形ABCD、正五边形ABCDE分别是⊙O的内接正三角形、内接正四边形、内接正五边形，点M，N分别从点B，C开始，以相同的速度在⊙O上逆时针运动．

(1)、在图1中，求∠APB的度数．

(2)、在图2中，求∠APB的度数；在图3中，求∠APB的度数．

(3)、根据前面的探索，若多边形ABCDE……是⊙O的正n边形，则∠APB的度数是(用含n的代数式表示)．

查看试题解析
23. 如图1，正五边形 $A B C D E$ 内接于 $⊙ O$ ，阅读以下作图过程，并回答下列问题：作法如图2．
①作直径 $A F$ ．
②以点 $F$ 为圆心， $F O$ 为半径作圆弧，与 $⊙ O$ 交于点 $M ， N$ ．
③连结 $A M ， M N ， N A$ ．

(1)、求 $∠ A B C$ 的度数．

(2)、 $△ A M N$ 是正三角形吗？请说明理由．

(3)、从点 $A$ 开始，以 $D N$ 长为半径，在 $⊙ O$ 上依次截取点，再依次连结这些等分点，得到正 $n$ 边形，求 $n$ 的值．

查看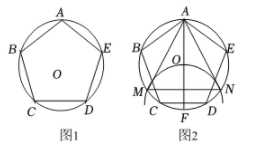试题解析
24. 如图

如图1，正五边形ABCDE内接于⊙O，阅读以下作图过程，并回答下列问题：

作法如图2.

1.作直径AF.

2.以F为圆心，FO为半径作圆弧，与⊙O交于点M，N.

3.连结AM，MN，NA.

(1)、求∠ABC的度数.

(2)、△AMN是正三角形吗？请说明理由.

(3)、从点A开始，以DN长为半径，在⊙O上依次截取点，再依次连结这些分点，得到正n边形，求n的值.

查看试题解析
25. 如图（1），正五边形ABCDE与⊙O相切于点A，点C在⊙O上．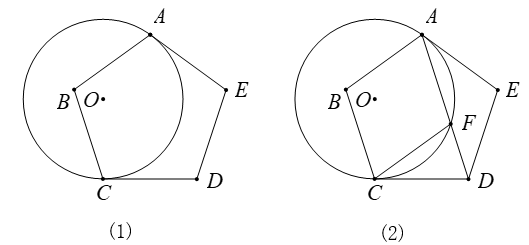

(1)、求证：CD是⊙O的切线；

(2)、若⊙O的半径为5，求劣弧AC的长度；

(3)、如图（2），连接AD交⊙O于点F．求证：四边形ABCF是菱形．

查看试题解析

26. 如图，正三角形、正方形、正六边形等正 $n$ 边形与圆的形状有差异，我们将正 $n$ 边形与圆的接近程度称为“接近度”．

(1)、角的 “接近度” 定义：设正 $n$ 边形的每个内角的度数为 $m^{\circ}$ ，将正 $n$ 边形的 “接近度”定义为 $| 180 - m |$ ．于是 $| 180 - m |$ 越小，该正 $n$ 边形就越接近于圆．
①若 $n = 3$ ，则该正 $n$ 边形的 “接近度”等于.
②若 $n = 20$ ，则该正 $n$ 边形的“接近度”等于.
③当“接近度”等于时，正 $n$ 边形就成了圆．

(2)、边的 “接近度” 定义：设一个正 $n$ 边形的外接圆的半径为 $R$ ，正 $n$ 边形的中心到各边的距离为 $d$ ，将正 $n$ 边形的“接近度”定义为 $|\frac{d}{R} - 1|$ ．分别计算当 $n = 3 ， n = 6$ 时边的“接近度”，并猜测当边的“接近度”等于多少时，正 $n$ 边形就成了圆．

查看试题解析

27.

如何设计计算油漆用量的方案？
素材1	小明家的一面墙壁由边长为1分米的小正方形密铺而成，上面画了如图所示的心形图案.他现在准备将心形图案的内部刷上红色的油漆，已知刷1平方分米需要0.02升的油漆.
素材2	奥地利数学家皮克证明了格点多边形的面积公式，格点多边形的面积S与格点多边形内的格点数a和边界上的格点数b有关，面积公式可表示为 $S = m a + n b - 1$ （其中m，n为常数）.示例：如图2，格点多边形内的格点数 $a = 4$ ，边界上的格点数 $b = 6$ ，格点多边形的面积 $S = 6$ .
问题解决
任务1	在图3中画一个格点多边形，并计算它的格点多边形内的格点数a，边界上的格点数b和面积S.	$a =$ ▲ $b =$ ▲ $S =$ ▲
任务2	得出格点多边形的面积公式	根据图2和图3的数据，求常数m，n的值.
任务3	计算油漆的用量	求需要红色油漆多少升？

查看试题解析

28. 问题再现
现实生活中，镶嵌图案在地面、墙面乃至于服装面料设计中随处可见.对于单种多边形的镶嵌，主要研究了三角形、正方形、正六边形的镶嵌问题.今天我们把正多边形的镶嵌作为研究问题的切入点，提出其中几个问题，共同来探究.
我们知道，可以单独用正三角形、正方形或正六边形镶嵌平面.如图，用正方形镶嵌平面，可以发现在一个顶点 O 周围围绕着4个正方形的内角.
试想：如果用正六边形来镶嵌平面，在一个顶点周围应该围绕着    ▲        个正六边形的内角.
问题提出
如果我们要同时用两种不同的正多边形镶嵌平面，可能设计出几种不同的组合方案?
问题解决
猜想1：是否可以同时用正方形、正八边形两种正多边形组合进行平面镶嵌?
分析：我们可以将此问题转化为数学问题来解决.从平面图形的镶嵌中可以发现，解决问题的关键在于分析能同时用于完整镶嵌平面的两种正多边形的内角特点.具体地说，就是在镶嵌平面时，一个顶点周围围绕的各个正多边形的内角恰好拼成一个周角.
验证1：在镶嵌平面时，设围绕某一点有x个正方形和y个正八边形的内角可以拼成一个周角.根据题意，可得方程：
$90 x + \frac{(8 - 2) \times 180}{8} \cdot y = 360,$ 整理得：2x+3y=8，
我们可以找到唯一一组适合方程的正整数解为 ${\begin{matrix} x = 1, \\ y = 2 . \end{matrix}$
结论1：镶嵌平面时，在一个顶点周围围绕着1个正方形和2个正八边形的内角可以拼成一个周角，所以同时用正方形和正八边形两种正多边形组合可以进行平面镶嵌.
猜想2：是否可以同时用正三角形和正六边形两种正多边形组合进行平面镶嵌?若能，请按照上述方法进行验证，并写出所有可能的方案；若不能，请说明理由.
验证2：    ▲
结论2：    ▲
上面，我们探究了同时用两种不同的正多边形组合镶嵌平面的部分情况，仅仅得到了一部分组合方案，相信同学们用同样的方法，一定会找到其他可能的组合方案.
问题拓展
请你依照上面的研究方式，探索出一个同时用三种不同的正多边形组合进行平面镶嵌的方案，并写出验证过程.
猜想3：    ▲
验证3：    ▲
结论3：    ▲

查看试题解析

【青海卷】备战2026年中考数学真题变式阶梯训练第23~25题

一、原题23

二、变式1基础

三、变式2巩固

四、变式3提高

五、原题24

六、变式1（基础）

七、变式2（巩固）

八、变式3（提高）

九、原题25

十、变式1[基础]

十一、变式2[巩固]

十二、变式3[提高]

组别	成绩/分	额数（人数）
1	75≤x＜80	10
2	80≤x＜85	a
3	85≤x＜90	35
4	90≤x＜95	25
5	95≤x≤100	b

组别	时长x/分钟	频数
A	0≤x＜20	20
B	20≤x<40	40
C	40≤x＜60	▲
D	60≤x<80	60
E	80≤x≤100	10

类型	人数	百分比
纯电	$m$	$54 %$
混动	$n$	$a %$
氢燃料	3	$b %$
油车	5	$c %$