【青海卷】备战2026年中考数学真题变式阶梯训练第21~22题-在线组卷题库

1. 数学实践
【问题背景】中国传统农业智慧遇上现代数学模型.“豇豆不上架，产量少一半”的农谚流传至今，现代科学揭示了其秘密：当支架与地面形成( $6 5^{\circ}$ °夹角时，既能在早春聚热防冻害，又能在盛夏分散强光，就像给豇豆装了智能遮阳篷.
【问题呈现】用两根竹竿交叉，斜插入地面，交叉点在何处会使支架与地面形成65°夹角?
【模型建立】环节一：数据收集
两根竹竿长度均为 1.8米，插入地下的部分为 0.3米，竹竿与地面接触点间距为 0.6米且与地面所形成的夹角均为 $6 5^{\circ} .$
环节二：数学抽象
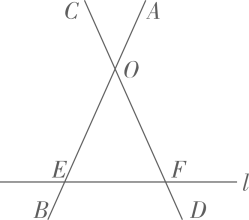
如图：已知线段AB与CD交于点O ， AB ， CD与直线l分别交于点E ， F ， $A B = C D = 1.8 m,$ $B E = D F = 0.3 m, ∠ A E F = ∠ C F E = 6 5^{\circ}, E F = 0.6 m,$ 求 OE的长度.(结果精确到0.1，参考数据： $s i n 6 5^{\circ} \approx 0.91, c o s 6 5^{\circ} \approx 0.42, t a n 6 5^{\circ} \approx 2.14)$
【模型求解】

【问题总结】交叉点O 距顶端A的长度即 OA为 m时，支架与地面形成( $6 5^{\circ}$ 夹角，这样更贴合作物的生长规律.

查看试题解析

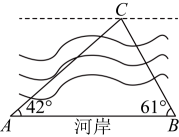
2. 小明和小军两位同学对某河流的宽度进行测量，如图所示，两人分别站在同侧河岸上的点 $A$ 、 $B$ 处，选取河对岸的一块石头 $C$ 作为测量点（点 $A 、 B 、 C$ 在同一水平面内），小明同学在点 $A$ 处测得 $∠ B A C$ 为 $42 °$ ，小军同学在点 $B$ 处测得 $∠ A B C$ 为 $61 °$ ，两人之间的距离 $A B$ 为60米，求此河流的宽度．（参考数据： $s i n 42 ° \approx 0.67, t a n 42 ° \approx 0.90, s i n 61 ° \approx 0.87, t a n 61 ° \approx 1.80$ ）

查看试题解析
3. 小明寒假去乡下爷爷家，看到爷爷家房屋结构如图所示，好奇的小明想测量房屋最高点 $F$ 到地面 $A C$ 的距离 $F P$ ．他发现 $P$ 为 $B C$ 的中点，并根据实际情况测量出房屋的宽度 $B C$ 为 $5$ 米，屋檐 $D E$ 的长为 $0.8$ 米，屋檐 $D E$ 与地面平行，并在与 $F$ ， $D$ 处于同一直线的 $A$ 点处测得 $∠ D A B = 25 °$ ， $∠ E A B = 23 ° ．$ 请根据以上信息，帮小明求出 $F$ 到地面 $B C$ 的距离 $F P ．$ (结果精确到 $0.1$ 米；参考数据： $\sin 25 ° \approx 0.42$ ， $\cos 25 ° \approx 0.90$ ， $\tan 25 ° \approx 0.46$ ， $\sin 23 ° \approx 0.39$ ， $\cos 23 ° \approx 0.92$ ， $\tan 23 ° \approx 0.42$ )．

查看试题解析
4. 如图1是一辆高空作业升降车在某次工作时的实景图，图2是它的示意图．已知点A，B，C，D，E，F，G在同一平面内，四边形 $A B C D$ 为矩形，点B，C在地面l上， $E F$ ， $F G$ 是可以伸缩的起重臂，转动点E到l的距离为2米．当 $E F = 2$ 米， $F G = 8$ 米， $∠ A E F = 60 °$ ， $∠ E F G = 90 °$ 时，求操作平台G到l的距离．

查看试题解析

5. 问题情境：筒车是我国古代发明的一种水利灌溉工具，既经济又环保.明代科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(如图①).假定在水流量稳定的情况下，筒车上的每一个盛水筒都沿逆时针方向做匀速圆周运动，每旋转一周用时 120秒.
问题设置：把筒车抽象为一个半径为2米的⊙O，如图②.OM始终垂直于水平面，在某一时刻，某盛水筒恰好位于水面A处，此时∠AOM=30°，经过95秒后该盛水筒运动到点B处.
问题解决：

(1)、求∠BOM的度数；

(2)、求该盛水筒旋转至B处时，它到水面的距离.(结果精确到0.1米，参考数据： $\sqrt{2} \approx 1.414, \sqrt{3} \approx 1.732)$

查看试题解析
6. 综合与实践
【阅读材料】
如图1，在锐角△ABC中， $∠ A ， ∠ B ， ∠ C$ 的对边长分别为a， b，c，则有 $\frac{a}{s i n A} = \frac{b}{s i n B} = \frac{c}{s i n C} .$ 这是解三角形的重要结论，可用于解决实际问题.
【问题提出】
万绿湖是广东省重要的生态屏障和饮用水水源地.某综合与实践小组要绘制一幅万绿湖局部平面示意图，现需要知道湖中A，B两岛间的实际距离.由于地形原因，无法利用训距仪直接测量，该小组对这一问心进行了探究.
【方案设计】
工具：测角仪、测距仪、无人机(只能刮角度、水平面高度).
测量过程：
步骤1：如图2，在空旷地找一点C：
步骤2：利用无人机多次测量并取平均值测得∠A≈43°，∠B≈51°；
步骤3：利用测距仪多次测量并取平均值测得BC≈341m， AC≈388.5m.

(1)、【问题解决】
请你利用【阅读材料】中的结论计算Δ. B两岛间的距离.
(参考数据： $s i n 4 3^{\circ} \approx 0.682 ， s i n 5 1^{\circ} \approx 0.777 ， s i n 8 6^{\circ} \approx 0.998)$

(2)、【评价反思】
设计其他方案计算λ、B两岛间的距离.要求：选用【方案设计】中的工具，写出你的方案和所用的数学知识.

查看试题解析

7. 城市轨道交通发展迅猛，为市民出行带来极大方便，某校“综合实践”小组想测得轻轨高架站的相关距离，数据勘测组通过勘测得到了如下记录表：

综合实践活动记录表
活动内容	测量轻轨高架站的相关距离
测量工具	测倾器，红外测距仪等
过程资料		相关数据及说明：图中点 $A, B, C, D$ ， $E, F$ 在同平面内，房顶 $A B$ ，吊顶 $C F$ 和地面 $D E$ 所在的直线都平行，点 $F$ 在与地面垂直的中轴线 $A E$ 上， $∠ B C D = 98 °$ ， $∠ C D E = 97 °, A E = 8.5 m, C D = 6.7 m$ ．
成果梳理	……

请根据记录表提供的信息完成下列问题：

(1)、求点

C

到地面

D E

的距离；

(2)、求顶部线段

B C

的长．（结果精确到

0.01 m

，参考数据：

sin 15 ° \approx 0.259

，

\cos 15 ° \approx 0.966

，

\tan 15 ° \approx 0.268

，

\sin 83 ° \approx 0.993, \cos 83 ° \approx 0.122, tan 83 ° \approx 8.144

）

查看试题解析

8. 在物理实验中，光线从空气中射入液体中会发生折射现象. 某学习小组设计了如图所示的实验. 水槽横截面为矩形 MNFD， $M N = 80 c m$ ， O 为水槽水面 DF 的中点，水深 $D M = 20 c m$ . 如图（a），小明同学从高出水面 30 cm 的 A 处发出一束激光，射到水槽水面上的 O 处，光在水中的路径为 OB，C 为水槽底部 MN 的中点，测得 $B C = 10 c m$ .（图中点 M，C，B，N 在同一直线上；点 A，P，R，D，M 在同一直线上）

(1)、【问题初探】
如图（a）， $α$ ， $β$ 分别为入射角、折射角，则 $t a n α =$ ， $t a n β =$ .

(2)、【深入探究】
小组成员探究如何才能使折射光线经过点 C.
① 小张同学设计了如图（b）所示的实验，在保持光线出发点 A、入射角、折射角不变的条件下，通过增加水面高度，使得折射光线经过点 C，请求出增加的水面高度 DP 的值.
② 小刚同学设计了如图（c）所示的实验，在保持入射角、折射角不变的条件下，通过把光线的出发点从点 A 降至点 R，也能使得折射光线经过点 C. 请求出下降高度 AR 的值.

(3)、【问题拓展】
小组讨论后，认为在保持入射角、折射角不变的条件下，将光线出发点的高度降低 x cm，同时增加水面高度 y cm，也能使得折射光线经过点 C，请求出 y 与 x 之间的函数关系.

查看试题解析
9. 根据以下素材，设计落地窗的遮阳篷．
素材1：如图1，小浩家的窗户朝南，窗户的高度 $A B = 2 m$ ，此地一年中的正午时刻，太阳光与地平面的最小夹角为 $α$ ，最大夹角为 $β$ ．如图2，小浩设计直角形遮阳篷 $B C D$ ，点 $C$ 在 $A B$ 的延长线上， $C D ⊥ A C$ ，它既能最大限度地使冬天温暖的阳光射入室内（太阳光与 $B D$ 平行），又能最大限度地遮挡夏天炎热的阳光（太阳光与 $A D$ 平行）．
素材2：小浩查阅资料，计算出 $\tan α = \frac{1}{3}$ ， $\tan β = \frac{4}{3}$ （ $∠ E A M = α$ ， $∠ D A M = β$ ，如图2）．
素材3：如图3，为了美观及实用性，小浩再设计出圆弧形可伸缩遮阳篷（劣弧 $C D$ 延伸后经过点 $B$ ， $D F$ 段可伸缩， $F$ 为 $\overset{⌢}{C D}$ 的中点）， $B C$ ， $C D$ 的长保持不变．
【任务1】如图2，求 $B C$ ， $C D$ 的长．
【任务2】如图3，求劣弧 $C D$ 的弓高．
【任务3】如图3，若某时太阳光与地平面的夹角 $γ$ 的正切值 $\tan γ = \frac{2}{3}$ ，要最大限度地使阳光射入室内，求遮阳篷点 $D$ 上升高度的最小值（点 $D^{'}$ 到 $C D$ 的距离）．

查看试题解析

10. 如图，线段AB经过圆心O ，交⊙O于点A ， C ， AD为⊙O的弦，连接BD ， ∠A=∠B=30°.

(1)、求证：直线 BD是⊙O的切线；

(2)、已知BC=2，求 $\hat{D C}$ 的长(结果保留π).

查看试题解析

11.
已知：如图，AB是⊙O的直径，BC是和⊙O相切于点B的切线，⊙O的弦AD平行于OC．求证：DC是⊙O的切线.

查看试题解析
12. 已知：如图，PA是⊙O的切线，A是切点．B为⊙O上一点，PA＝PB．求证：PB是⊙O的切线．

查看试题解析
13. 如图，点O在∠APB的平分线上，⊙O与PA相切于点C.求证：直线PB与⊙O相切。

查看试题解析

14. 如图， $A B$ 是 $⊙ O$ 的直径， $B E$ 与 $⊙ O$ 相切于点 $B$ ，点 $D$ 是 $⊙ O$ 上一点，连接 $E D$ 并延长交 $B A$ 的延长线于点 $P$ ．连接 $B D$ 、 $E O$ 相交于点 $G$ ，延长 $E O$ 交 $⊙ O$ 于点 $F$ ．若 $E O$ 平分 $∠ D E B$ ，且 $E G ⊥ B D$ ．

(1)、求证： $E P$ 是 $⊙ O$ 的切线；

(2)、若 $A P = 3$ ， $P D = 6$ ，求 $O A$ 及 $E F$ 的长．

查看试题解析
15. 如图，在 $△ A B C$ 中， $B D$ 是 $∠ A B C$ 的平分线，以点D为圆心的 $⊙ D$ 与 $B A$ 相切于点A，分别与 $A C ， B D$ 相交于点E，F．

(1)、求证： $B C$ 是 $⊙ D$ 的切线．

(2)、若 $∠ A B C = 80 °$ ， $A D = 18$ ，求 $\overset{⏜}{E F}$ 的长．

查看试题解析
16. 如图，在四边形ABCD 中，. $B D = C D, ∠ C = ∠ B A D .$ .以AB 为直径的⊙O经过点D，且与边CD 交于点 E，连接AE，BE.

(1)、求证：BC为⊙O 的切线；

(2)、若 $A B = \sqrt{10}, s i n ∠ A E D = \frac{\sqrt{10}}{10},$ 求BE 的长.

查看试题解析

17. 如图，AB 为⊙O的直径，点C 为⊙O 上一点，连接AC，BC，点 D为AB延长线上一点，连接CD，且∠BCD=∠A.

(1)、求证：CD 是⊙O 的切线.

(2)、若⊙O 的半径为 $\sqrt{5}$ ， △ABC 的面积为2 $\sqrt{5}$ ，求CD 的长.

(3)、在(2)的条件下，点 E 为⊙O 上一点，连接CE 交线段OA 于点F，若 $\frac{E F}{C F} = \frac{1}{2},$ 求 BF 的长.

查看试题解析
18. 如图，AB 为⊙O 的直径，点 D 是 $\hat{A E}$ 上的一点，且∠BDE=∠CBE，BD 与AE 交于点F.

(1)、求证：BC 是⊙O的切线.

(2)、若 BD 平分∠ABE，求证： $D E^{2} = D F \cdot D B .$

(3)、在(2)的条件下，延长ED，BA 交于点P，若PA=AO，DE=2，求 PD的长和⊙O 的半径.

查看试题解析
19. 如图①，D为⊙O上一点，点C在直径BA 的延长线上，且∠CDA=∠CBD.

(1)、判断直线CD 与⊙O 的位置关系，并说明理由.

(2)、若 $t a n ∠ A D C = \frac{1}{2}, A C = 2,$ 求⊙O 的半径.

(3)、如图②，在(2)的条件下，∠ADB 的平分线DE 交⊙O 于点E，交AB 于点F，连接BE.求sin∠DBE 的值.

查看试题解析

【青海卷】备战2026年中考数学真题变式阶梯训练第21~22题

一、原题21

二、变式1基础

三、变式2巩固

四、变式3提高

五、原题22

六、变式1（基础）

七、变式2（巩固）

八、变式3（提高）