【青海卷】备战2026年中考数学真题变式阶梯训练第19~20题
试卷更新日期:2025-10-17 类型:二轮复习
一、原题19
-
1. 如图, 直线. 与x轴交于点A(1,0),与y轴交于点B , 与反比例函数 (m为常数, 的图象在第二象限交于点
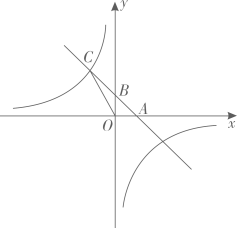 (1)、求反比例函数的解析式;(2)、 求 的面积.
(1)、求反比例函数的解析式;(2)、 求 的面积.二、变式1基础
-
2. 一次函数与反比例函数的图象都经过点 , 求一次函数和反比例函数的解析式.3. 若与都是反比例函数图象上的点,求n的值.4. 已知平面直角坐标系中,一次函数(为常数,)的图象与反比例函数(为常数,)的图象都经过点和点 , 求的值.
三、变式2巩固
-
5. 如图,反比例函数与一次函数是常数, , 的图象交于点.
 (1)、分别求出两个函数的表达式.(2)、根据图象,当时,请直接写出的取值范围:.6. 如图,在平面直角坐标系中,点 , 都在反比例函数的图象上,直线与轴,轴分别相交于点 , .
(1)、分别求出两个函数的表达式.(2)、根据图象,当时,请直接写出的取值范围:.6. 如图,在平面直角坐标系中,点 , 都在反比例函数的图象上,直线与轴,轴分别相交于点 , . (1)、求的值,并根据图象直接写出当直线在反比例函数图象上方时,的取值范围.(2)、求证: .7. 如图,已知反比例函数的图像与正比例函数的图像交于点A(1,2)和点B.
(1)、求的值,并根据图象直接写出当直线在反比例函数图象上方时,的取值范围.(2)、求证: .7. 如图,已知反比例函数的图像与正比例函数的图像交于点A(1,2)和点B. (1)、求反比例函数的表达式;(2)、点C(-2,0),判断直线BC与反比例函数图像除点B以外是否还有其他不同的交点,并说明理由。
(1)、求反比例函数的表达式;(2)、点C(-2,0),判断直线BC与反比例函数图像除点B以外是否还有其他不同的交点,并说明理由。四、变式3提高
-
8. 在平面直角坐标系xOy中,反比例函数的图象经过点A(1,5),点A,B关于原点对称.该函数图象上另有两点M1 , M2 , 它们的横坐标分别为m,m+n,其中m>1,n>0.依次作直线AM1 , BM1与y轴分别交于点C1 , D1 , 直线AM2 , BM2与y轴分别交于点C2 , D2.记OC1﹣OD1=d1 , OC2﹣OD2=d2 .(1)、若m=2,求OC1的长;(2)、求代数式(m+n)•d2的值;(3)、当m(d1﹣d2)=2d2 , 3(d1+d2)=2n3时,求点D2关于直线AM2对称的点P的坐标.9. 如图,直线与双曲线交于 , 两点.
 (1)、求和直线的表达式;(2)、根据函数图象直接写出不等式的解集;(3)、求△的面积.10. 如图,一次函数的图象与反比例函数的图象相交于两点.
(1)、求和直线的表达式;(2)、根据函数图象直接写出不等式的解集;(3)、求△的面积.10. 如图,一次函数的图象与反比例函数的图象相交于两点. (1)、求一次函数和反比例函数的表达式;(2)、根据图象直接写出时,的取值范围;(3)、过点作直线 , 交反比例函数图象于点 , 连结 , 求的面积.
(1)、求一次函数和反比例函数的表达式;(2)、根据图象直接写出时,的取值范围;(3)、过点作直线 , 交反比例函数图象于点 , 连结 , 求的面积.五、原题20
-
11. 如图, 在 中,点O , D分别是边AB , BC的中点,过点A作 交DO的延长线于点 E , 连接AD , BE.
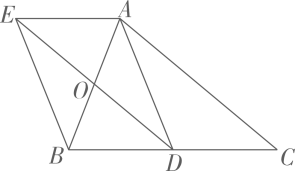 (1)、求证:四边形AEBD是平行四边形;(2)、若AB=AC , 试判断四边形AEBD的形状;并证明.
(1)、求证:四边形AEBD是平行四边形;(2)、若AB=AC , 试判断四边形AEBD的形状;并证明.六、变式1(基础)
-
12. 如图,已知四边形为平行四边形,将线段两端分别延长至点 , , 使得 , 求证:四边形是平行四边形.
 13. 如图,在平行四边形中,E,F分别是 , 的中点,求证: .
13. 如图,在平行四边形中,E,F分别是 , 的中点,求证: .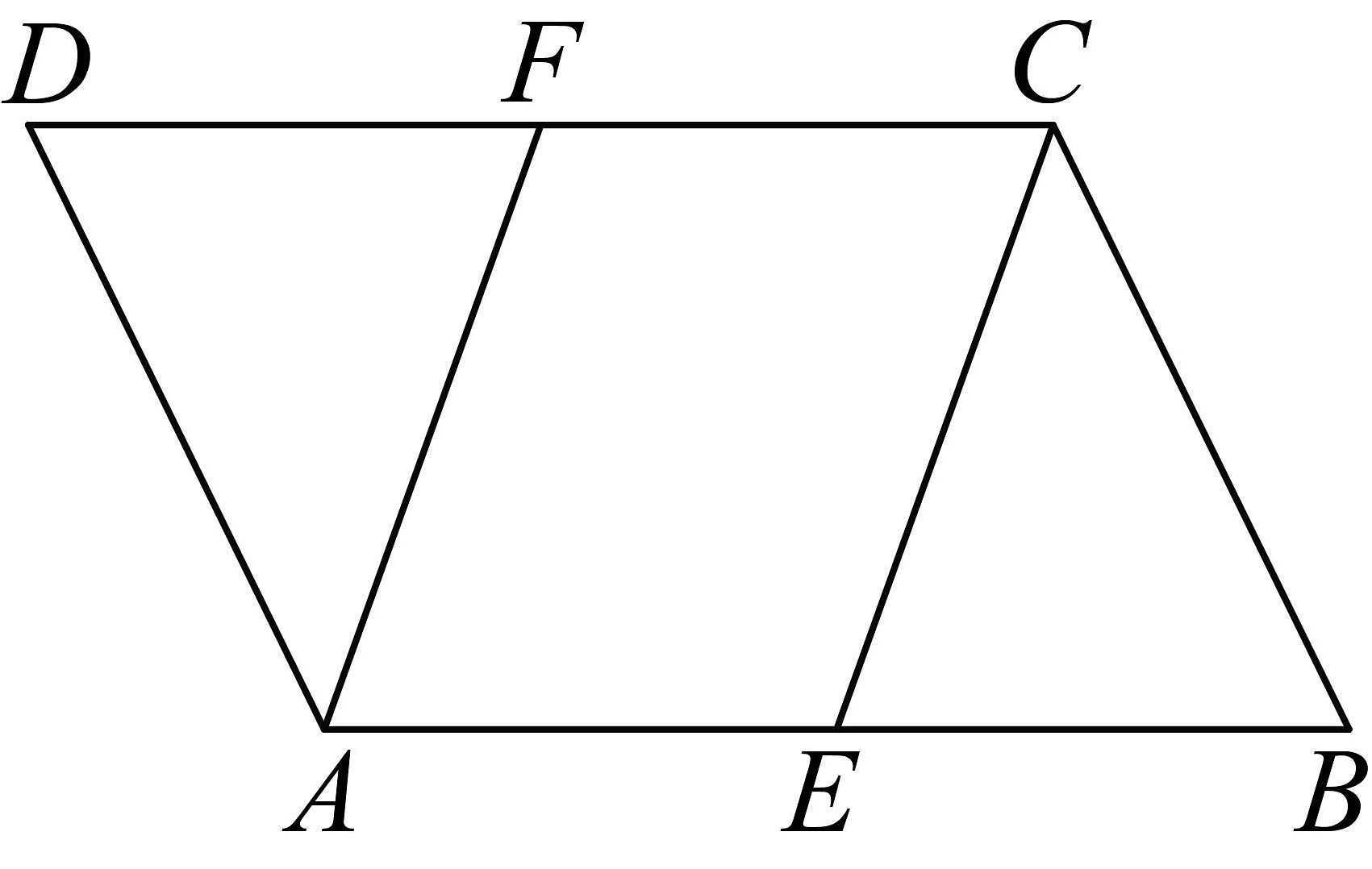 14. 如图,在中,点分别在上,且 . 求证:四边形是平行四边形.
14. 如图,在中,点分别在上,且 . 求证:四边形是平行四边形.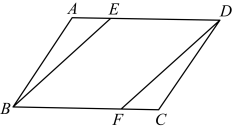
七、变式2(巩固)
-
15. 如图,在四边形中, , , , , 垂足分别为点E,F.
 (1)、求证:四边形是平行四边形;(2)、若点E,F是的三等分点, , , 求四边形的面积.16. 已知□ABCD。
(1)、求证:四边形是平行四边形;(2)、若点E,F是的三等分点, , , 求四边形的面积.16. 已知□ABCD。 (1)、如图1,E是AD上一点,以点C为圆心,AE的长为半径作弧,交BC于点F,连结AF,CE。求证:四边形AFCE是平行四边形。(2)、图1中□AFCE的四个顶点在□ABCD的边上,这样的四边形叫□ABCD的内接四边形。在图2中用直尺和圆规作一个□ABCD的内接菱形(保留作图痕迹)。17. 如图, 中,O是对角线的中点, 过点O作直线分别交于点E , F , 交的延长线分别于点 G , H , 连接 .
(1)、如图1,E是AD上一点,以点C为圆心,AE的长为半径作弧,交BC于点F,连结AF,CE。求证:四边形AFCE是平行四边形。(2)、图1中□AFCE的四个顶点在□ABCD的边上,这样的四边形叫□ABCD的内接四边形。在图2中用直尺和圆规作一个□ABCD的内接菱形(保留作图痕迹)。17. 如图, 中,O是对角线的中点, 过点O作直线分别交于点E , F , 交的延长线分别于点 G , H , 连接 . (1)、求证:四边形是平行四边形;(2)、当时,且 , , , 求的面积.
(1)、求证:四边形是平行四边形;(2)、当时,且 , , , 求的面积.八、变式3(提高)
-
18. 如图 1,已知线段 , 用无刻度的直尺和圆规作 .
以下是小颖同学的作法:
如图 2,先作的平分线 , 以点A为圆心,长为半径画弧,交于点 E , 连接并延长,再以点A为圆心,长为半径画弧,交射线于点D , 连接 , 则四边形为平行四边形.
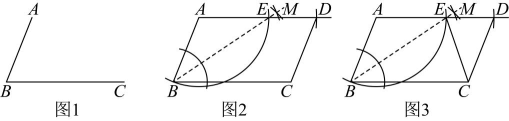 (1)、小颖的作法是否正确?若正确,请给出证明.(2)、在图 1 中作一个与小颖不同的方法的(保留作图痕迹,不需要证明).(3)、如图 3,在小颖同学的作法的条件下,连结 , 若 , 求四边形的面积.19. 如图 1,在四边形 ABCD 中, , .
(1)、小颖的作法是否正确?若正确,请给出证明.(2)、在图 1 中作一个与小颖不同的方法的(保留作图痕迹,不需要证明).(3)、如图 3,在小颖同学的作法的条件下,连结 , 若 , 求四边形的面积.19. 如图 1,在四边形 ABCD 中, , .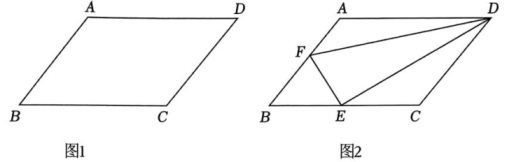 (1)、求证:四边形 ABCD 是平行四边形;(2)、在(1)的条件下,如图 2,若 F 为 AB 边上一点,E 为 BC 边上的中点,连结 DF, EF, DE,若 , 证明 .(3)、在(1)的条件下,若 F 为 AB 边上的中点,E 为 BC 边上的一点,连结 DF, EF, DE,若 , 请直接写出线段 BE,CE,ED之间的数量关系.20. 如图1,在平行四边形中,是上一点,连结 , 使 , 是上一点,满足 .
(1)、求证:四边形 ABCD 是平行四边形;(2)、在(1)的条件下,如图 2,若 F 为 AB 边上一点,E 为 BC 边上的中点,连结 DF, EF, DE,若 , 证明 .(3)、在(1)的条件下,若 F 为 AB 边上的中点,E 为 BC 边上的一点,连结 DF, EF, DE,若 , 请直接写出线段 BE,CE,ED之间的数量关系.20. 如图1,在平行四边形中,是上一点,连结 , 使 , 是上一点,满足 .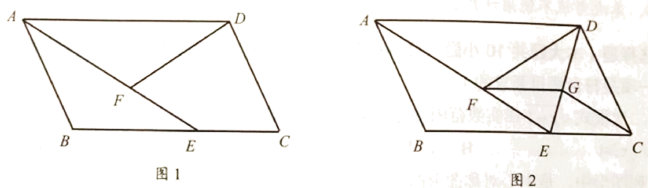 (1)、求证: .(2)、如图2,连结 , 过点作交于点 , 连结 .
(1)、求证: .(2)、如图2,连结 , 过点作交于点 , 连结 .①求证:四边形为菱形.
②若 , , , 求的长.
-
-