浙教版数学八(上) 第二章第3-4节 等腰三角形性质与判定定理 周测卷
试卷更新日期:2025-10-15 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如图,在中, , 平分 , 若 , 则的度数为( )
 A、 B、 C、 D、2. 如图,一束太阳光线平行照射在放置于地面的等边上,若 , 则的度数为( )
A、 B、 C、 D、2. 如图,一束太阳光线平行照射在放置于地面的等边上,若 , 则的度数为( ) A、 B、 C、 D、3. 如图所示,中, , , 要求用圆规和直尺作图,把它分成两个三角形,其中一个三角形是等腰三角形.其作法错误的是( )A、
A、 B、 C、 D、3. 如图所示,中, , , 要求用圆规和直尺作图,把它分成两个三角形,其中一个三角形是等腰三角形.其作法错误的是( )A、 B、
B、 C、
C、 D、
D、 4. 如图,在中, , 的平分线交于点D,过点D作交于点E,交于点F.若 , , , 则的周长是( )
4. 如图,在中, , 的平分线交于点D,过点D作交于点E,交于点F.若 , , , 则的周长是( ) A、17 B、20 C、22 D、265. 如图,D、E为等边△ABC边AB、BC上的点,连结DE,∠ADE和∠DEC的角平分线恰好过 AC边上同一点F。若要知道△ABC 的周长,只需要知道下列哪个三角形的周长?该三角形是( )
A、17 B、20 C、22 D、265. 如图,D、E为等边△ABC边AB、BC上的点,连结DE,∠ADE和∠DEC的角平分线恰好过 AC边上同一点F。若要知道△ABC 的周长,只需要知道下列哪个三角形的周长?该三角形是( ) A、△ADF B、△BDE C、△CEF D、△DEF6. 如图,在中, , , 点、在上,将、分别沿、翻折,点、分别落在点、的位置,再将、分别沿、翻折,点与点恰好重合于点 , 则的度数是( )
A、△ADF B、△BDE C、△CEF D、△DEF6. 如图,在中, , , 点、在上,将、分别沿、翻折,点、分别落在点、的位置,再将、分别沿、翻折,点与点恰好重合于点 , 则的度数是( )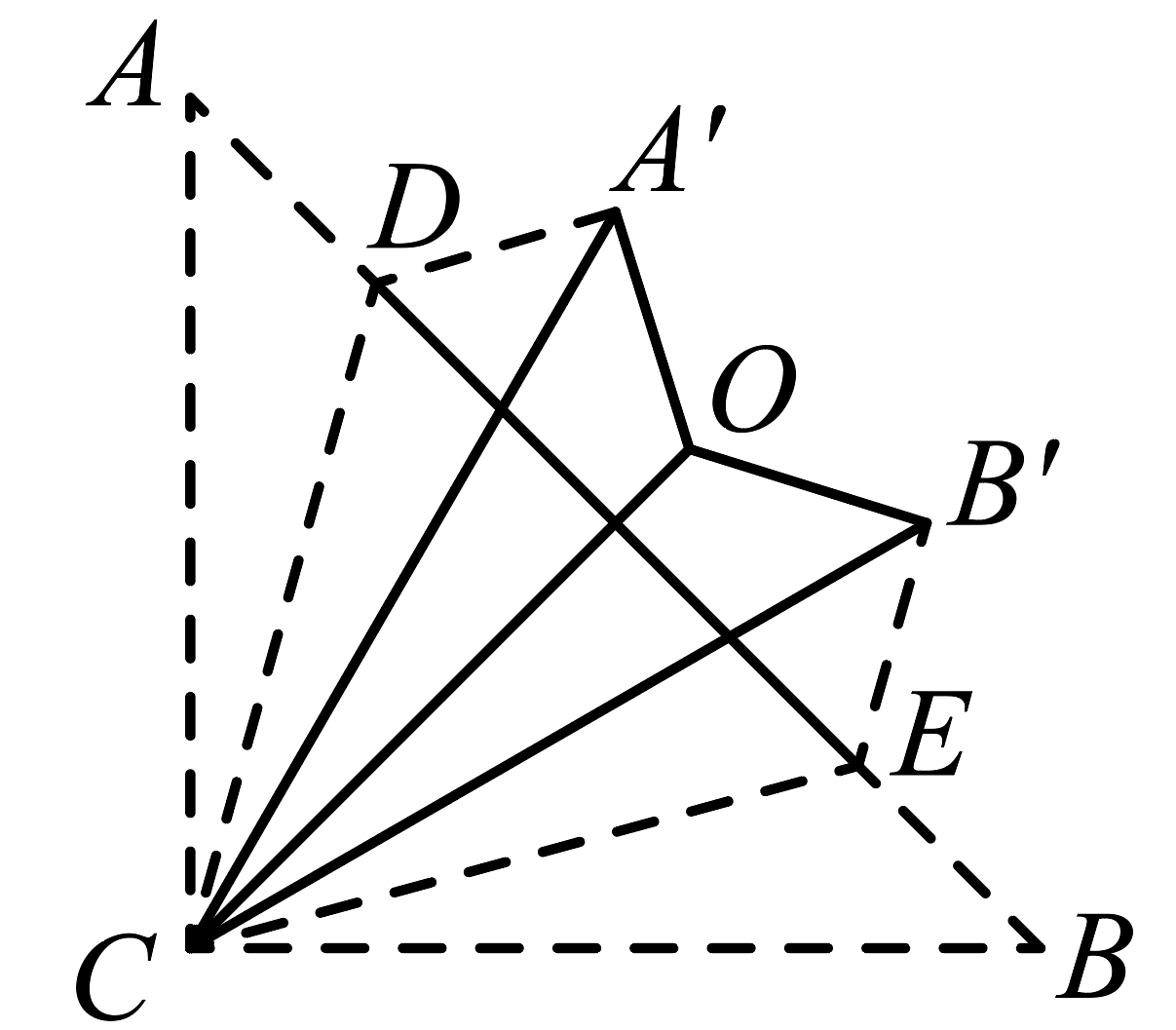 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共15分)
-
7. 如图,中, , 点E为的中点,点D在上,且、相交于点F,若 , 则等于 .
 8. 如图,∠A=52°,O是AB,AC的垂直平分线的交点,则∠OCB= .
8. 如图,∠A=52°,O是AB,AC的垂直平分线的交点,则∠OCB= .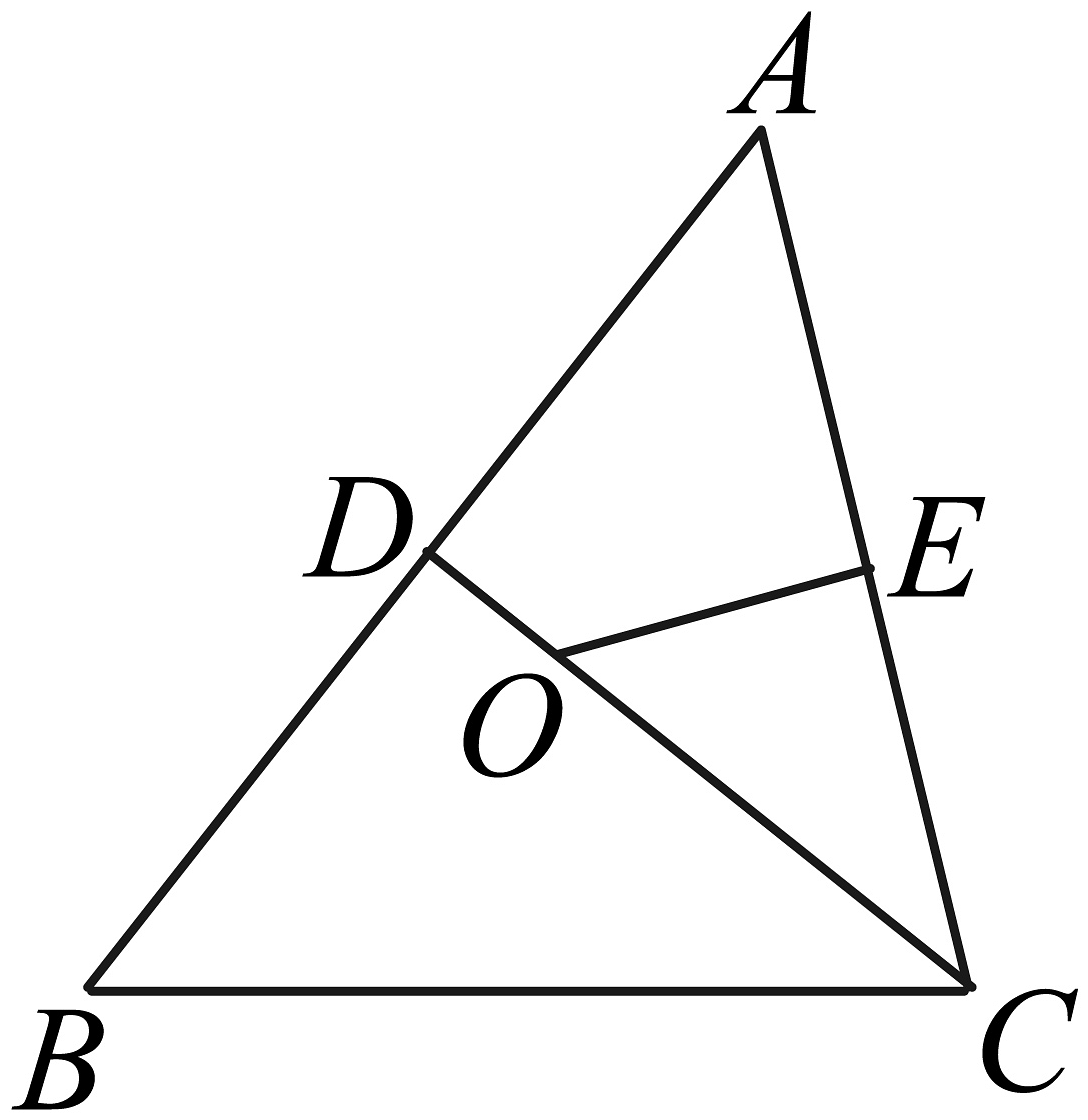 9. 如图,在中, , 是的平分线.若P,Q分别是和上的动点,则的最小值是 .
9. 如图,在中, , 是的平分线.若P,Q分别是和上的动点,则的最小值是 . 10. 为等边三角形,点E在边上, , 在射线上取点D,使 , 连接并延长交射线于点F,则下列说法正确的是: .
10. 为等边三角形,点E在边上, , 在射线上取点D,使 , 连接并延长交射线于点F,则下列说法正确的是: .①当时,为等腰三角形;
②;
③在边上存在点E,使;
④ .
三、解答题(共8题,共75分)
-
11. 如图,在中, , 平分 , .
 (1)、求的度数;(2)、若 , 垂足为 , 交于点 , 求的度数.12. 如图,在中,边的垂直平分线分别交于D、E.
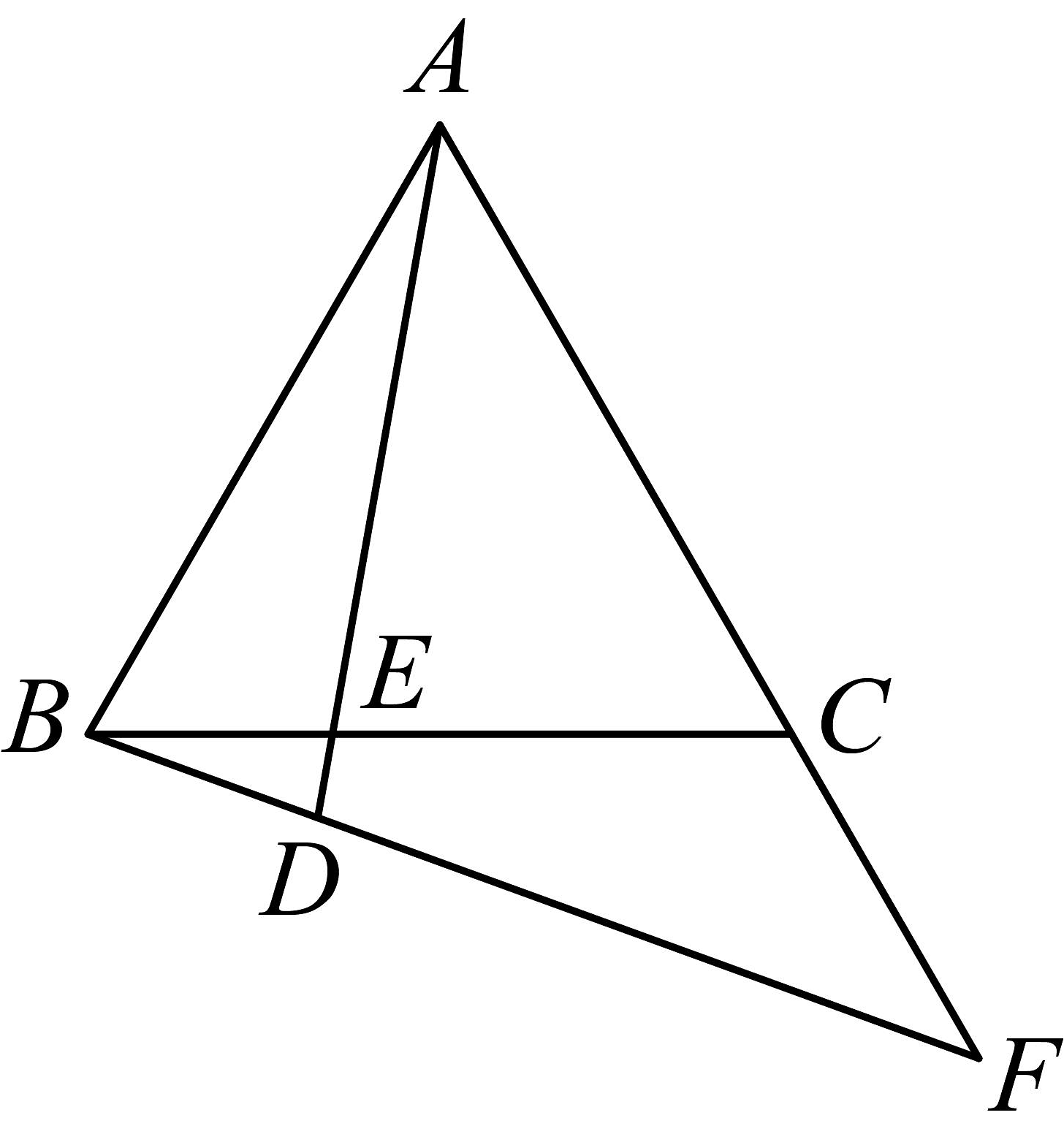
(1)、求的度数;(2)、若 , 垂足为 , 交于点 , 求的度数.12. 如图,在中,边的垂直平分线分别交于D、E. (1)、若 , 求的周长.(2)、若 , 求的度数.13. 如图,中,AC的垂直平分线分别交BC、AC于点E、F,且CE,作交BC于点.
(1)、若 , 求的周长.(2)、若 , 求的度数.13. 如图,中,AC的垂直平分线分别交BC、AC于点E、F,且CE,作交BC于点.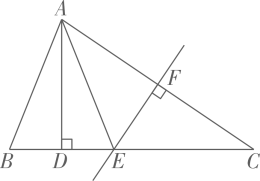 (1)、若 , 求的度数.(2)、若的周长为17cm,求DC的长.14. 如图, , , , .
(1)、若 , 求的度数.(2)、若的周长为17cm,求DC的长.14. 如图, , , , . (1)、求的度数;(2)、判断的形状,并说明理由.15. 如图, ,点 在 上.
(1)、求的度数;(2)、判断的形状,并说明理由.15. 如图, ,点 在 上. (1)、求证: ;(2)、若 平分 ,求 的度数.16. 如图, 是等腰三角形, 是等边三角形,且点B,D,E,C在同一条直线上.
(1)、求证: ;(2)、若 平分 ,求 的度数.16. 如图, 是等腰三角形, 是等边三角形,且点B,D,E,C在同一条直线上. (1)、若AD=2,BC=12,求CE的长;(2)、以AC为腰在AC下方作等腰 使AF=AC,连接EF,BF.若BD=EF.求证: 是等边三角形.17. 已知 , 以为边在外作等腰 , 其中 .
(1)、若AD=2,BC=12,求CE的长;(2)、以AC为腰在AC下方作等腰 使AF=AC,连接EF,BF.若BD=EF.求证: 是等边三角形.17. 已知 , 以为边在外作等腰 , 其中 . (1)、如图1,以为边也在外作等腰 , 其中 , 连接与 , 交于点 . 若 , 则______;(2)、如图2,若 , 是等边三角形, , , 求的长;(3)、如图3,若为锐角,作于 , 当时,试判断与的数量关系,并证明你的结论.18. 【探究学习】
(1)、如图1,以为边也在外作等腰 , 其中 , 连接与 , 交于点 . 若 , 则______;(2)、如图2,若 , 是等边三角形, , , 求的长;(3)、如图3,若为锐角,作于 , 当时,试判断与的数量关系,并证明你的结论.18. 【探究学习】规定①:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“类似三角形”.
规定②:从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“类似三角形”,我们把这条线段叫做这个三角形的“完美分割线”.

【概念理解】
(1)如图1,在中, , 平分 , 则与 (填“是”或“不是”)互为“类似三角形”.
(2)如图2,在中,平分 , , . 求证:为的完美分割线;
【概念应用】
(3)在中, , 是的完美分割线,直接写出的度数.