浙教版数学九(上)第一章 二次函数 单元测试基础卷
试卷更新日期:2025-10-14 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 下列函数中是二次函数的是( )A、 B、 C、 D、2. 将抛物线 先向左平移 2 个单位,再向下平移 3 个单位,则平移后的抛物线解析式为( )A、 B、 C、 D、3. 对于抛物线 , 下列判断正确的是( )A、抛物线的开口向上 B、抛物线的顶点坐标是 C、当时 D、对称轴为直线4. 函数y=x2-4的图象与y轴的交点坐标是( )A、(2,0) B、(-2,0) C、(0,4) D、(0,-4)5. 将二次函数的图象向左平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( )A、 B、 C、 D、6. 下表是一组二次函数的自变量x与函数值y的对应值:
x
1
1.1
1.2
1.3
1.4
y
-1
-0.49
0.04
0.59
1.16
那么方程的一个近似根是( )
A、1 B、1.1 C、1.2 D、1.37. 在函数的图象上有三点, , 则下列各式中,正确的是( )A、 B、 C、 D、8. 如图是二次函数 图象的一部分,图象过点 A(-3,0),对称轴为直线 , 给出四个结论:① ;② ;③ ;④ , 其中正确结论是( )
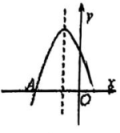 A、②④ B、①④ C、②③ D、①③9. 如图,二次函数( , , 为常数,)的图象与轴交于点 , 对称轴是直线 , 有以下结论:①;②若点和点都在抛物线上,则;③(为任意实数);④ . 其中正确的有( )
A、②④ B、①④ C、②③ D、①③9. 如图,二次函数( , , 为常数,)的图象与轴交于点 , 对称轴是直线 , 有以下结论:①;②若点和点都在抛物线上,则;③(为任意实数);④ . 其中正确的有( ) A、1个 B、2个 C、3个 D、4个10. 已知二次函数的对称轴为 , 当时,y的取值范围是 . 则的值为( )A、或 B、或 C、 D、
A、1个 B、2个 C、3个 D、4个10. 已知二次函数的对称轴为 , 当时,y的取值范围是 . 则的值为( )A、或 B、或 C、 D、二、填空题(每题3分,共15分)
-
11. 抛物线与y轴交点的坐标为 , 与x轴交点的坐标为 .12. 二次函数的最小值为 .13. 如图,要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端点安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为处达到最高,高度为 , 水柱落地处离池中心距离为 , 则水管的长度是 .
 14. 若一个点的纵坐标是横坐标的2倍,则称这个点为“二倍点”,如: , , 等都是“二倍点”.在的范围内,若二次函数的图像上至少存在一个“二倍点”,则的取值范围是 .15. 抛物线的对称轴为直线 , 部分图象如图所示,下列判断中:①;②;③;④若点均在抛物线上,则;⑤ . 其中正确的序号是(填写正确的序号).
14. 若一个点的纵坐标是横坐标的2倍,则称这个点为“二倍点”,如: , , 等都是“二倍点”.在的范围内,若二次函数的图像上至少存在一个“二倍点”,则的取值范围是 .15. 抛物线的对称轴为直线 , 部分图象如图所示,下列判断中:①;②;③;④若点均在抛物线上,则;⑤ . 其中正确的序号是(填写正确的序号).
三、解答题(共8题,共75分)
-
16. 已知二次函数的图象经过点 .(1)、求c的值;(2)、判断点是否在该函数的图象上,并说明理由.17. 在平面直角坐标系中,抛物线经过和两点.(1)、求该抛物线的解析式;(2)、求该抛物线的对称轴和顶点坐标.18. 如图,现打算用60m的离笆围成一个“日"字形菜园ABCD(含隔离栏EF),菜园的一面靠墙MN(墙MN可利用的长度为39m)(离笆的宽度忽略不计)
 (1)、菜园面积可能为252m2吗?若可能,求边长AB的长,若不可能,请说明理由:(2)、因场地限制,菜园的宽度AB不能超过8m,求该菜园面积的最大值.19. 在一次高尔夫球的练习中,小成在O处击球,其飞行路线满足抛物线 , 其中是球的飞行高度,是球飞出的水平距离,结果球离球洞的水平距离还有2 m.
(1)、菜园面积可能为252m2吗?若可能,求边长AB的长,若不可能,请说明理由:(2)、因场地限制,菜园的宽度AB不能超过8m,求该菜园面积的最大值.19. 在一次高尔夫球的练习中,小成在O处击球,其飞行路线满足抛物线 , 其中是球的飞行高度,是球飞出的水平距离,结果球离球洞的水平距离还有2 m.
(1)请求出抛物线的顶点坐标;
(2)请求出球洞离击球点的距离;
(3)若小成再一次从O处击球,要想让球飞行的最大高度不变且球刚好进洞,则球飞行路线应满足怎样的抛物线,求出其解析式,
20. 某商家销售一种成本为20元的商品,销售一段时间后发现,每天的销量y(件)与当天的销售单价(元)满足一次函数关系,并且当时,;当时, . 物价部门规定,该商品的销售单价不能超过45元.(1)、求y关于的函数关系式;(2)、当销售单价定为多少元时,商家销售该商品每天获得的利润是8000元?(3)、求商家销售该商品每天获得的最大利润.21. 已知关于x的二次函数(1)、若该函数的图象与x轴的交点坐标是 , 求的值;(2)、若该函数的图象的顶点纵坐标为3,①用含b的代数式表示c;
②当时,y的取值范围是 , 求c的取值范围.
22. 【项目】小车沿斜面运动中路程 与时间 的关系.
图1是小车从料面上静止滑下的实验装置,斜面刻度值单位为分米。 小温和小州共同填写了如下实验记录表。1 (秒)
0
2
3
(分米)
0
4
9

 (1)、小温发现,路程 与时间 可采用一次函数,反比例函数,二次函数中的一种进行刻画,请通过实验数据在图 2 中描点画图,判断可以采用的函数模型,并求出 关于 的函数表达式.(2)、若斜面足够长,请通过计算说明小车在斜面上第一个 5 秒和第二个 5 秒通过的路程之差。(3)、小州说:把单位时间设为 1 秒,还可以研究第 秒内通过的路程 (分米)与第 秒之间的函数关系。
(1)、小温发现,路程 与时间 可采用一次函数,反比例函数,二次函数中的一种进行刻画,请通过实验数据在图 2 中描点画图,判断可以采用的函数模型,并求出 关于 的函数表达式.(2)、若斜面足够长,请通过计算说明小车在斜面上第一个 5 秒和第二个 5 秒通过的路程之差。(3)、小州说:把单位时间设为 1 秒,还可以研究第 秒内通过的路程 (分米)与第 秒之间的函数关系。请写出一个路程 (分米)与第 秒之间的结论,井通过计算说明理由.
23. 综合与探究如图,在平面直角坐标系中,抛物线经过点 , , 连接 , 为抛物线部分上一动点(可与A , B两点重合),过点P作轴交直线于点M , 交x轴于点N .
 (1)、求抛物线和直线的解析式.(2)、①求线段的最大值.
(1)、求抛物线和直线的解析式.(2)、①求线段的最大值.②连接 , 当为等腰三角形时,求m的值.