浙教版数学八(上) 第一章 三角形 单元测试基础卷
试卷更新日期:2025-10-14 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 下面四个图形中,线段BE是⊿ABC的高的图是( )A、
 B、
B、 C、
C、 D、
D、 2. 对于命题“若a2>b2 , 则a>b”,下面四组关于a , b的值中,能说明这个命题是假命题的是( )A、a=3,b=2 B、a=-3,b=2 C、a=3,b=-1 D、a=-1,b=33. 如图,若两个三角形全等,图中字母表示三角形边长,则的度数为( )
2. 对于命题“若a2>b2 , 则a>b”,下面四组关于a , b的值中,能说明这个命题是假命题的是( )A、a=3,b=2 B、a=-3,b=2 C、a=3,b=-1 D、a=-1,b=33. 如图,若两个三角形全等,图中字母表示三角形边长,则的度数为( ) A、 B、 C、 D、4. 打碎的一块三角形玻璃如图所示,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( )
A、 B、 C、 D、4. 打碎的一块三角形玻璃如图所示,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( ) A、带①②去 B、带②③去 C、带③④去 D、带④去5. 如图,直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A、带①②去 B、带②③去 C、带③④去 D、带④去5. 如图,直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( ) A、1处 B、2处 C、3处 D、4处6. 如图,、E是直线上不重合的两点,是的角平分线,于点A,若的周长为10,则的周长可能是( )
A、1处 B、2处 C、3处 D、4处6. 如图,、E是直线上不重合的两点,是的角平分线,于点A,若的周长为10,则的周长可能是( )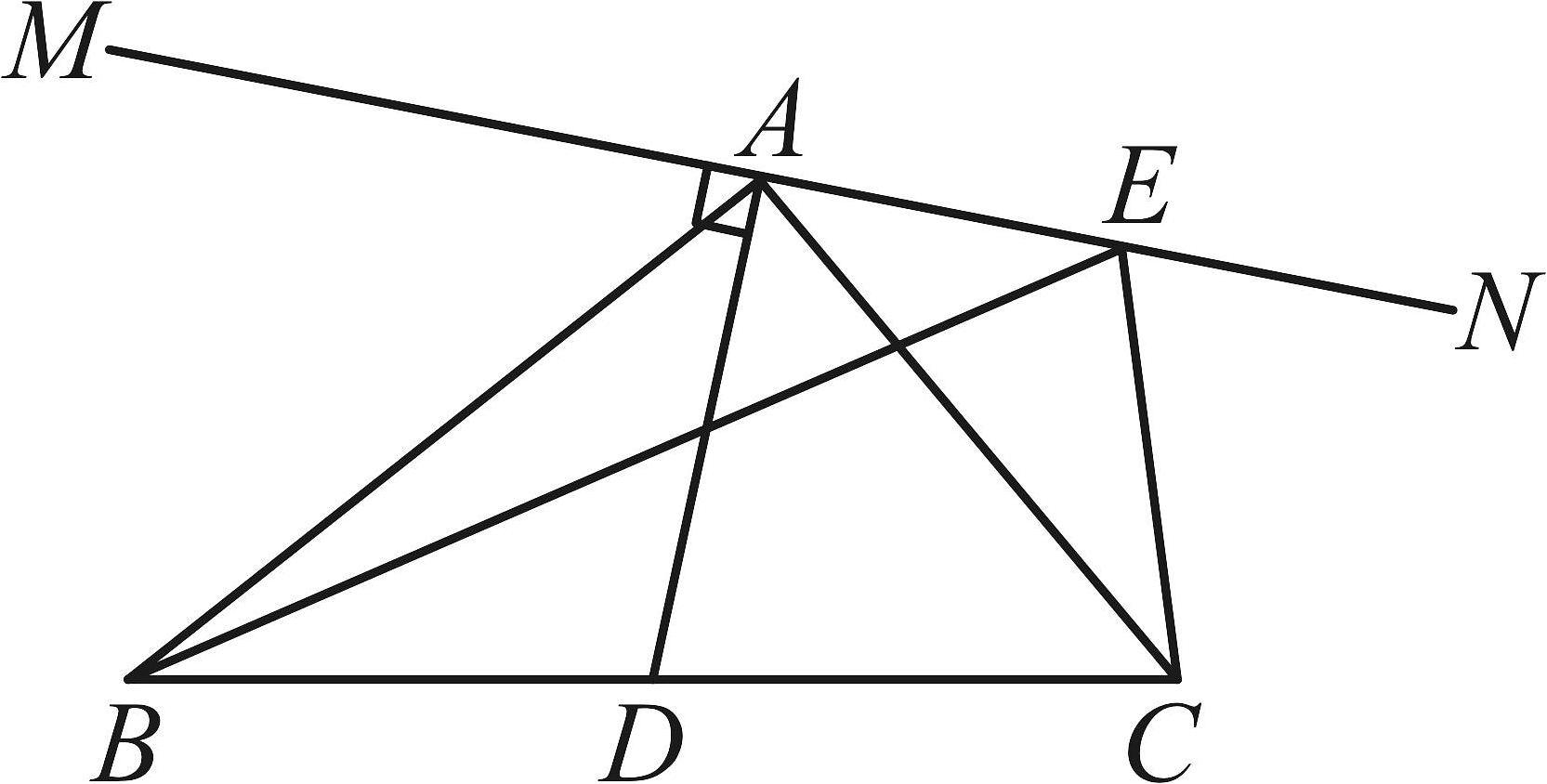 A、8 B、9 C、10 D、117. 如图,A、C、B三点在同一条直线上,和都是等边三角形,分别与交于点M、N,有如下结论:①;②;③;④是等边三角形;其中,正确结论的个数是( )
A、8 B、9 C、10 D、117. 如图,A、C、B三点在同一条直线上,和都是等边三角形,分别与交于点M、N,有如下结论:①;②;③;④是等边三角形;其中,正确结论的个数是( )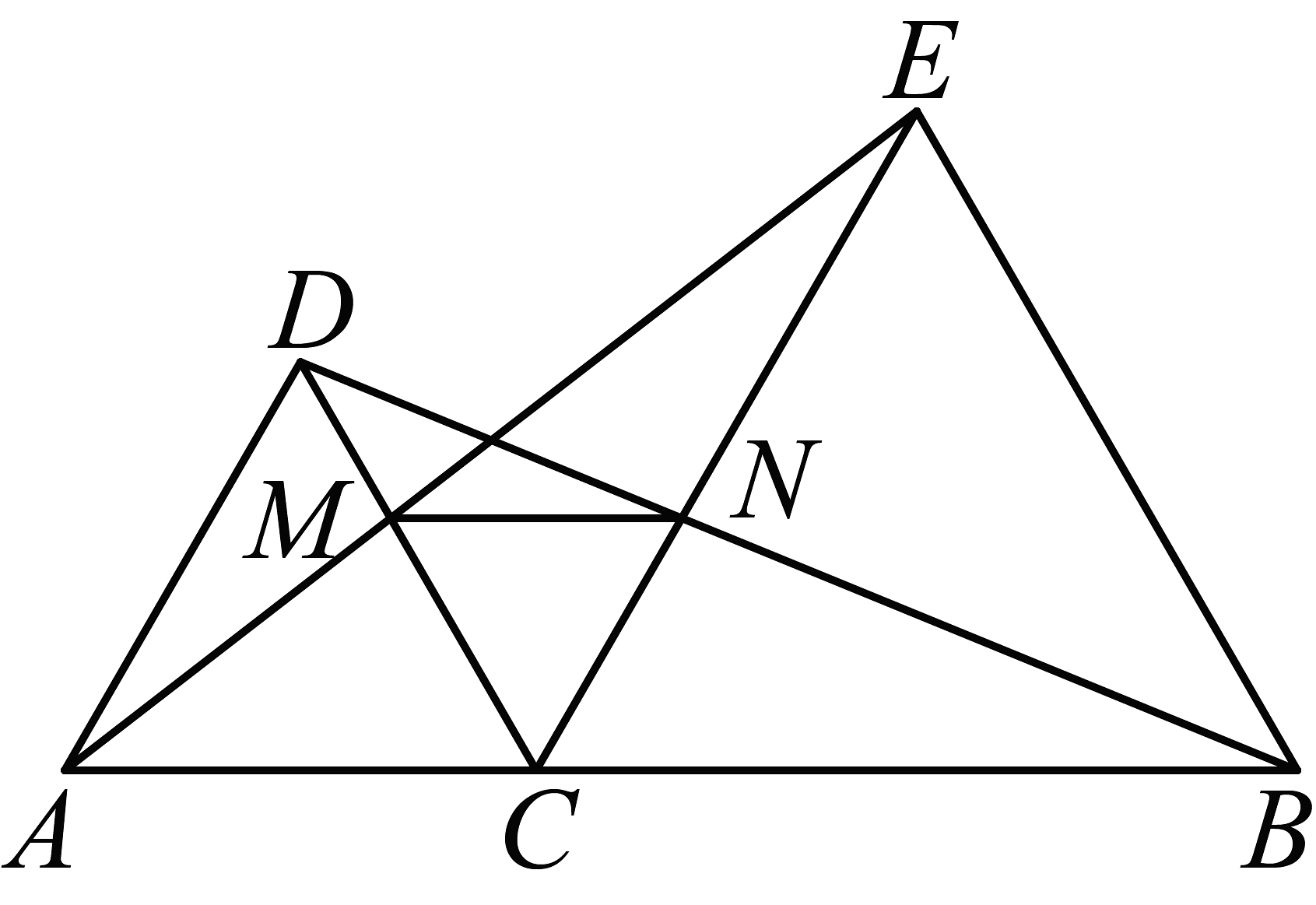 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每题3分,共15分)
-
8. 如图,在中,平分 , , 的面积为45,的面积为20,则的面积等于 .
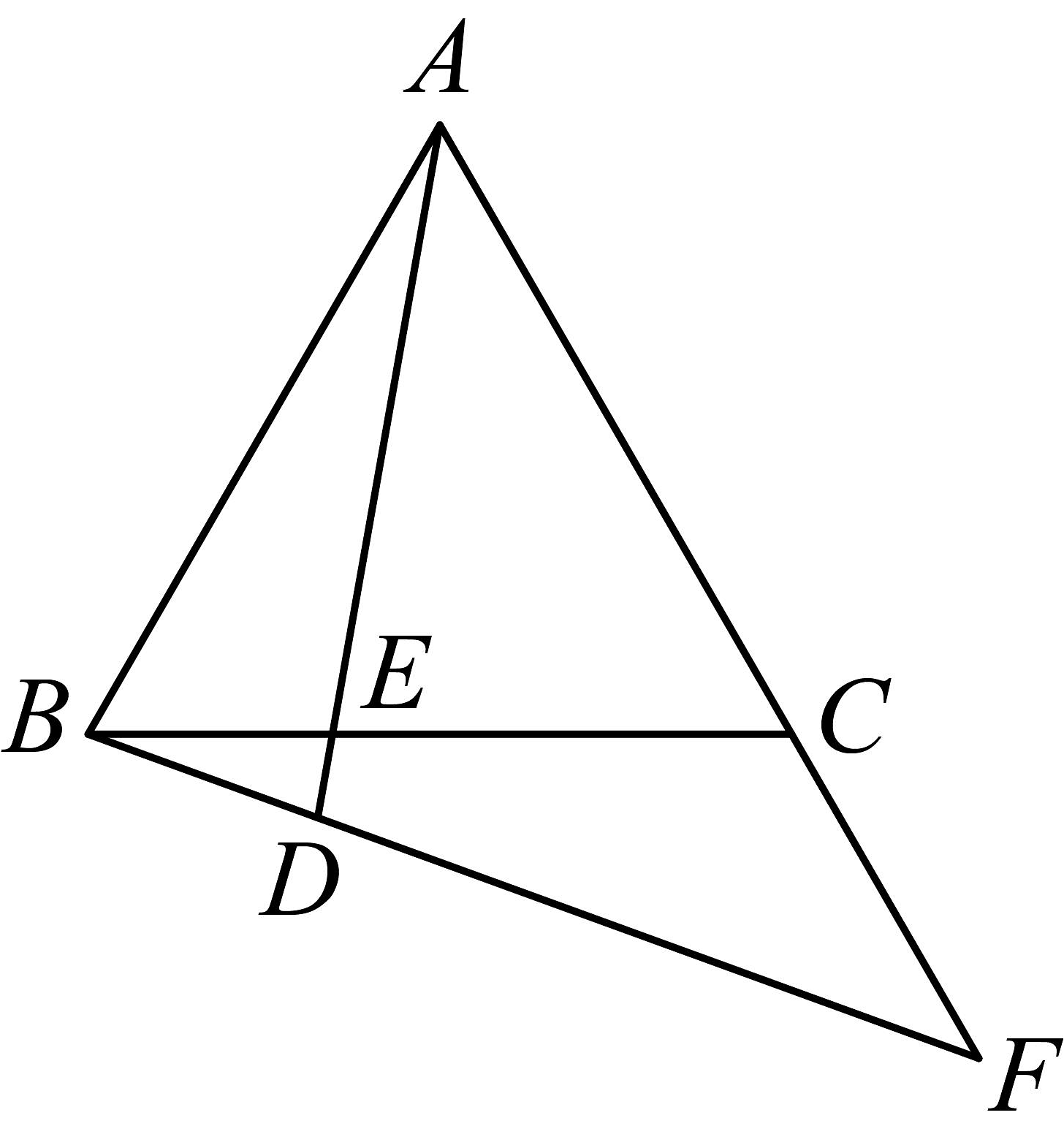
 9. 为等边三角形,点E在边上, , 在射线上取点D,使 , 连接并延长交射线于点F,则下列说法正确的是: .
9. 为等边三角形,点E在边上, , 在射线上取点D,使 , 连接并延长交射线于点F,则下列说法正确的是: .①当时,为等腰三角形;
②;
③在边上存在点E,使;
④ .
三、解答题(共8题,共75分)
-
10. 如图,已知△ABC≌△ADE .
 (1)、求证:∠1=∠2;(2)、当∠BED=50°时,求∠AEC的度数.11. 如图,已知:在和中,点A、E、F、C在同一直线上, , , .求证:.
(1)、求证:∠1=∠2;(2)、当∠BED=50°时,求∠AEC的度数.11. 如图,已知:在和中,点A、E、F、C在同一直线上, , , .求证:. 12. 如图,在中,边 , 的垂直平分线 , 分别交于点D,E.
12. 如图,在中,边 , 的垂直平分线 , 分别交于点D,E. (1)、若 , 求的周长.(2)、若 , 求的度数.
(1)、若 , 求的周长.(2)、若 , 求的度数.