2025年人教版数学八年级上册周测卷 (第十四章 第2-3节)培优卷
试卷更新日期:2025-10-13 类型:同步测试
一、选择题
-
1. 如图,小敏做了一个角平分仪 , 其中 , , 将仪器上的点A与的顶点R重合,调整和 , 使它们分别落在角的两边上,过点A、C画一条射线 , 就是的平分线.此角平分仪的画图原理是( )
 A、 B、 C、 D、2. 如图,中, , 平分 , , 点D到的距离为( )
A、 B、 C、 D、2. 如图,中, , 平分 , , 点D到的距离为( ) A、1 B、2 C、3 D、43. 如图是一款路灯及其平面示意图,已知AB=AD,CF=CG,B,D分别为 CF,CG 的中点, ∠ABF = 122°,∠BAE=59°,则∠ACD 的度数为 ( )
A、1 B、2 C、3 D、43. 如图是一款路灯及其平面示意图,已知AB=AD,CF=CG,B,D分别为 CF,CG 的中点, ∠ABF = 122°,∠BAE=59°,则∠ACD 的度数为 ( )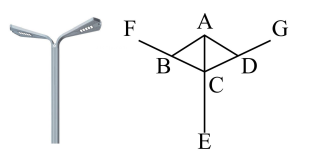 A、58° B、59° C、63° D、70°4. 在中, , 的角平分线交于点 , 则点到的距离是( )
A、58° B、59° C、63° D、70°4. 在中, , 的角平分线交于点 , 则点到的距离是( ) A、2 B、3 C、4 D、55. 如图,直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A、2 B、3 C、4 D、55. 如图,直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( ) A、1处 B、2处 C、3处 D、4处6. 如图,在中, , . 以A为圆心,为半径画弧交于点D;分别以C,D为圆心,大于长为半径画弧交于点E,射线交于点F,连结 , 则的度数为( )
A、1处 B、2处 C、3处 D、4处6. 如图,在中, , . 以A为圆心,为半径画弧交于点D;分别以C,D为圆心,大于长为半径画弧交于点E,射线交于点F,连结 , 则的度数为( ) A、 B、 C、 D、7. 如图,在中,分别延长边上的中线到 . 使 , 则下列说法:①;②;③;④四边形的面积是面积的3倍.其中正确的有( )
A、 B、 C、 D、7. 如图,在中,分别延长边上的中线到 . 使 , 则下列说法:①;②;③;④四边形的面积是面积的3倍.其中正确的有( ) A、①②③ B、①②④ C、①③④ D、②③④8. 如图,在中 , , D,E是BC上两点,且 , 过点A作 , 垂足是A,过点C作 , 垂足是C,CF交AF于点F,连接EF.给出下列结论:①;②;③若 , , 则;④ . 其中正确结论的字号是( )
A、①②③ B、①②④ C、①③④ D、②③④8. 如图,在中 , , D,E是BC上两点,且 , 过点A作 , 垂足是A,过点C作 , 垂足是C,CF交AF于点F,连接EF.给出下列结论:①;②;③若 , , 则;④ . 其中正确结论的字号是( ) A、①②③ B、②③④ C、①③④ D、①②④9. 如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②PF=PA;③AH+BD=AB;④S四边形ABDE=S△ABP,其中正确的是( )
A、①②③ B、②③④ C、①③④ D、①②④9. 如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②PF=PA;③AH+BD=AB;④S四边形ABDE=S△ABP,其中正确的是( ) A、①③ B、①②④ C、①②③ D、②③10. 如图,已知和都是等腰直角三角形, , , 交于点F,连接 , 下列结论:①;②;③;④平分;⑤ , 其中结论正确的序号是( )
A、①③ B、①②④ C、①②③ D、②③10. 如图,已知和都是等腰直角三角形, , , 交于点F,连接 , 下列结论:①;②;③;④平分;⑤ , 其中结论正确的序号是( ) A、①②③④ B、①②④⑤ C、①③④⑤ D、①②③⑤
A、①②③④ B、①②④⑤ C、①③④⑤ D、①②③⑤二、填空题
-
11. 在RtABC中,∠C=90°,若BC=6,AD平分∠BAC交BC于点D,BD=2CD,则点D到线段AB的距离为 .
 12. 如图,在2×2的正方形网格中,线段、的端点为格点,则°.
12. 如图,在2×2的正方形网格中,线段、的端点为格点,则°. 13. 如图,在中, , 高 , 交于点H.若 , , 则 .
13. 如图,在中, , 高 , 交于点H.若 , , 则 . 14. 如图,点B、C、E三点在同一直线上,且AB=AD,AC=AE,BC=DE,若 , 则∠3=°.
14. 如图,点B、C、E三点在同一直线上,且AB=AD,AC=AE,BC=DE,若 , 则∠3=°. 15. 如图,在中, , 的平分线与外角的平分线相交于点M,作的延长线得到射线 , 作射线 , 有下面四个结论:
15. 如图,在中, , 的平分线与外角的平分线相交于点M,作的延长线得到射线 , 作射线 , 有下面四个结论:①;
②;
③射线是的角平分线;
④ .
所有正确结论的序号是 .

三、解答题
-
16. 如图,已知 , .
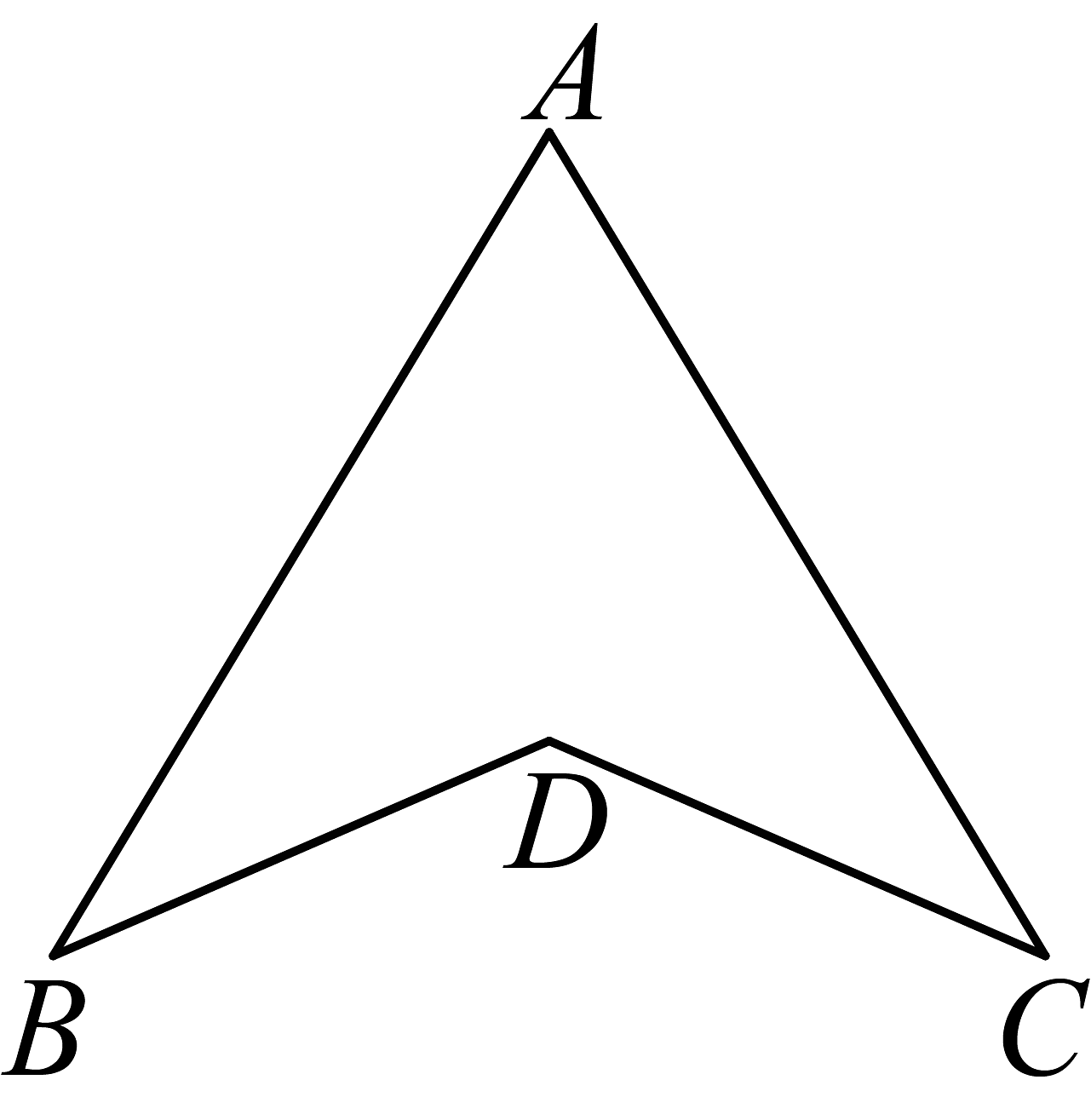 (1)、求证: . (提示:连接)(2)、当时,直接写出与之间的数量关系.17. 如图,小明同学拿着老师的等腰直角三角尺,摆放在两摞长方体教具之间, , , 每个小长方体教具高度均为 .
(1)、求证: . (提示:连接)(2)、当时,直接写出与之间的数量关系.17. 如图,小明同学拿着老师的等腰直角三角尺,摆放在两摞长方体教具之间, , , 每个小长方体教具高度均为 .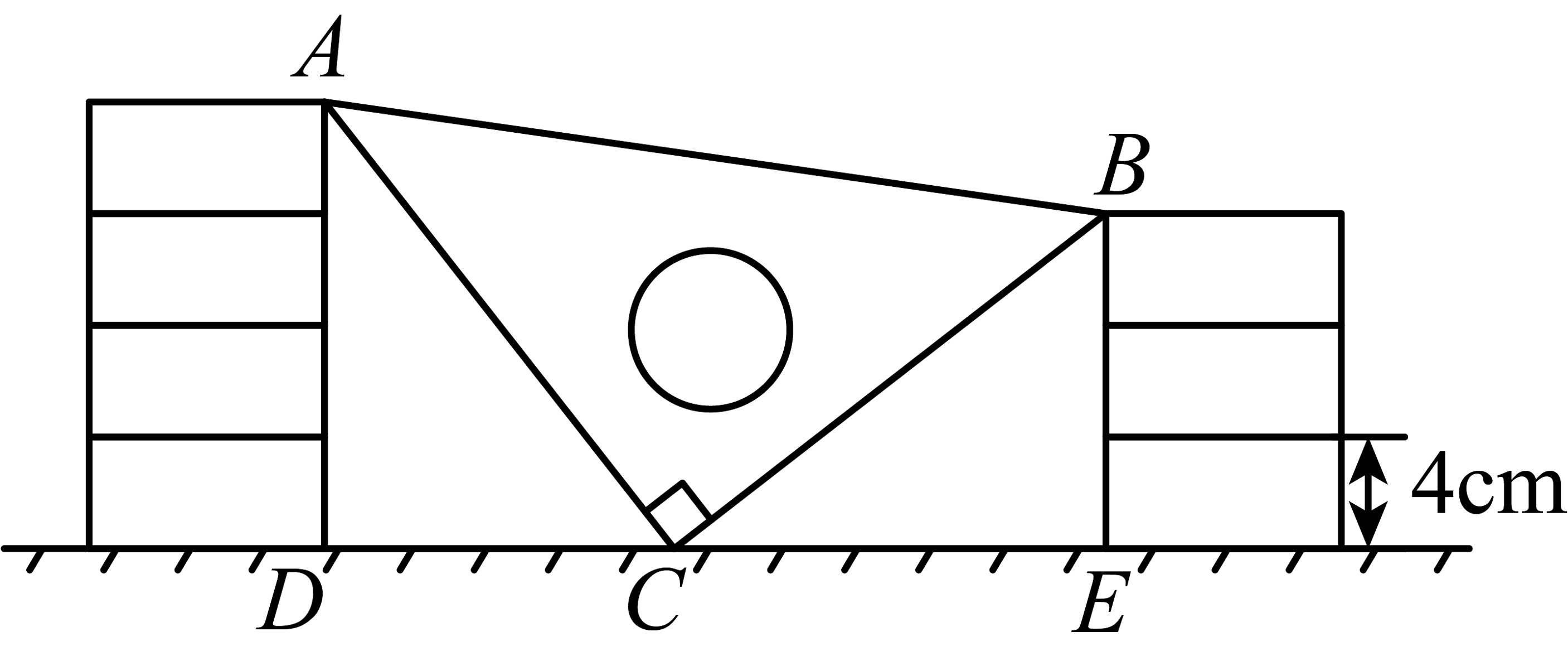 (1)、求证: .(2)、求的长.18. 如图,AB⊥CD于点D,E为CD上一点,连结AE,BC,AE=BC,DE=BD
(1)、求证: .(2)、求的长.18. 如图,AB⊥CD于点D,E为CD上一点,连结AE,BC,AE=BC,DE=BD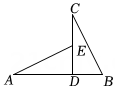 (1)、求证:△ADE≌△CDB:(2)、若AD=6,BD=2,求CE的长,19. 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.若∠ACD=114°,求∠MAB的度数.
(1)、求证:△ADE≌△CDB:(2)、若AD=6,BD=2,求CE的长,19. 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.若∠ACD=114°,求∠MAB的度数. 20. 如图, 在 Rt 中, , 点 在 的延长线上, 目 . 过点 作 , 与 的垂线 交于点 .
20. 如图, 在 Rt 中, , 点 在 的延长线上, 目 . 过点 作 , 与 的垂线 交于点 . (1)、 求证:(2)、 若 , 求 的长.21. 如图,四边形中,于点F,交于点E,连接 , 平分 .
(1)、 求证:(2)、 若 , 求 的长.21. 如图,四边形中,于点F,交于点E,连接 , 平分 . (1)、求证:;(2)、若 , 求的长.22. 【问题背景】在△ABC 和△BDE 中,AB=BC, BD = BE, ∠ABC = ∠DBE, 连 接CD,AE.
(1)、求证:;(2)、若 , 求的长.22. 【问题背景】在△ABC 和△BDE 中,AB=BC, BD = BE, ∠ABC = ∠DBE, 连 接CD,AE. (1)、【自主探究】如图①,当点 E 落在 BC 边上,且点A,E,D在同一条直线上时,若∠ABC=∠DBE=50°,则△BCD≌ , ∠ADC的度数为;(2)、【类比探究】如图②,大小不同的两个含45°的直角三角尺 ABC 和 BDE 的直角顶点重合于点 B,连接AE,CD,当点 C,D,E在同一条直线上时(点D 在点 C,E之间),请判断线段 CD 和 AE 的位置关系和数量关系,并说明理由.23. 我们定义:如图1,在四边形ABCD中,如果 , , 对角线BD平分 , 我们称这种四边形为“分角对补四边形”.
(1)、【自主探究】如图①,当点 E 落在 BC 边上,且点A,E,D在同一条直线上时,若∠ABC=∠DBE=50°,则△BCD≌ , ∠ADC的度数为;(2)、【类比探究】如图②,大小不同的两个含45°的直角三角尺 ABC 和 BDE 的直角顶点重合于点 B,连接AE,CD,当点 C,D,E在同一条直线上时(点D 在点 C,E之间),请判断线段 CD 和 AE 的位置关系和数量关系,并说明理由.23. 我们定义:如图1,在四边形ABCD中,如果 , , 对角线BD平分 , 我们称这种四边形为“分角对补四边形”. (1)、特例感知:如图1,在“分角对补四边形”ABCD中,当时,根据教材中一个重要性质直接可得 , 这个性质是;(填序号)
(1)、特例感知:如图1,在“分角对补四边形”ABCD中,当时,根据教材中一个重要性质直接可得 , 这个性质是;(填序号)①垂线段最短:②垂直平分线的性质;③角平分线的性质;④三角形内角和定理
(2)、猜想论证:如图2,当为任意角时,猜想DA与DC的数量关系,并给予证明;(3)、探究应用:如图3,在等腰中, , BD平分 ,求证:.