2025年人教版数学九年级上册周测卷（第二十二章第2-3节）培优卷

试卷更新日期：2025-10-13 类型：同步测试

进入出卷网下载

一、选择题

1. 已知二次函数y=ax²+bx+c中自变量x和函数y的部分对应值如下表：
x
…
-3
-2
-1
0
1
…
y
…
-1
-4
-1
8
23
…
则方程 ax²+bx+c=0的一个解x=t的取值范围下列可能的是（）

A、-3<t<-2 B、-2<t<-1 C、-1<t<0 D、0< t <1

查看试题解析
2. 深高小学部饲养了两只萌萌的羊驼，建筑队在学校一边靠墙处，计划用15米长的铁栅栏围成三个相连的长方形羊驼草料仓库，仓库总面积为y平方米，为方便取物，在各个仓库之间留出了1米宽的缺口作通道，在平行于墙的一边留下一个1米宽的缺口作小门，若设 $A B = x$ 米，则y关于x的函数关系式为（）

A、 $y = x (18 - 4 x)$ B、 $y = x (18 - 2 x)$ C、 $y = x (12 - 4 x)$ D、 $y = x 12 - 2 x$

查看试题解析
3. 将进货价格为35元的商品按单价40元售出时，能卖出200个．已知该商品单价每上涨1元，其销售量就减少5个．设这种商品的售价上涨x元时，获得的利润为y元，则下列关系式正确的是（　　）

A、y＝（x﹣35）（200﹣5x） B、y＝（x+40）（200﹣10x） C、y＝（x+5）（200﹣5x） D、y＝（x+5）（200﹣10x）

查看试题解析
4. 二次函数 $y = a x^{2} + b x + c$ 的图象与x轴交于点 $(1, 0)$ ， $(- 3, 0)$ ，则关于x的方程 $a x^{2} + b x + c = 0$ 的解为（）

A、 $x_{1} = 1$ ， $x_{2} = 3$ B、 $x_{1} = - 1$ ， $x_{2} = - 3$ C、 $x_{1} = - 1$ ， $x_{2} = 3$ D、 $x_{1} = 1$ ， $x_{2} = - 3$

查看试题解析
5. 函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，则函数 $y = c x^{2} - b x + a$ 的图象与 $x$ 轴的交点分别是 ( )

A、 $(- 1,0), (\frac{1}{3}, 0)$ B、 $(- \frac{1}{3}, 0), (1,0)$ C、 $(- 1,0), (3,0)$ D、 $(- 3,0), (1,0)$

查看试题解析
6. 如图所示，某工厂的大门是抛物线形水泥建筑物，大门的地面宽度为 $8 m$ ，两侧距地面 $3 m$ 高处各有一壁灯，两壁灯间的水平距离为 $6 m$ ，则厂门的高度约为（）

A、 $\frac{30}{7}$ B、 $\frac{38}{7}$ C、 $\frac{48}{7}$ D、 $\frac{50}{7}$

查看试题解析
7. 童装专卖店销售一种童装，若这种童装每天获利y（元）与销售单价x（元）满足关系 $y = - x^{2} + 50 x - 500$ ，若要想获得最大利润，则销售单价x为（）

A、25元 B、20元 C、30元 D、40元

查看试题解析
8. 如图，一工厂车间大门由抛物线和矩形 $A B C D$ 的三边组成，门的最大高度是 $4 .9m$ ， $A B = 10 m$ ， $B C = 2.4 m$ ，若有一个高为 $4m$ ，宽为 $2m$ 的长方体形状的大型设备要安装在车间，如果不考虑其他因素，设备的右侧离开门边多少米，此设备运进车间时才不会碰到门的顶部 $?$ （）

A、 $1 .8m$ B、 $1 .9m$ C、 $2m$ D、 $2 .1m$

查看试题解析
9. 已知二次函数 $y = (x - a) (x - b) - 1 (a < b)$ ，且 $x_{1}$ ， $x_{2}$ $(x_{1} < x_{2})$ 是方程 $(x - a) (x - b) - 1 = 0$ 的两个根，则实数a，b， $x_{1}$ ， $x_{2}$ 的大小关系为（）

A、 $a < x_{1} < b < x_{2}$ B、 $a < x_{1} < x_{2} < b$ C、 $x_{1} < a < x_{2} < b$ D、 $x_{1} < a < b < x_{2}$

查看试题解析
10. 已知二次函数 $y = a x^{2} + b x + c (a < 0)$ 的图象与 $x$ 轴交于不同两点，与 $y$ 轴的交点在 $y$ 轴正半轴，它的对称轴为直线 $x = 1$ ，有以下结论： ① $a b c < 0$ ， ② $2 a + b = 0$ ， ③抛物线上有两点 $P (x_{1}, y_{1})$ 和 $Q (x_{2}, y_{2})$ ，若 $x_{1} < 1 < x_{2}$ ，且 $x_{1} + x_{2} > 2$ ，则 $y_{1} > y_{2}$ ， ④设 $x_{1}$ ， $x_{2}$ 是方程． $a x^{2} + b x + c = 0$ 的两根，若 $a m^{2} + b m + c = p$ 则 $p (m - x_{1}) (m - x_{2}) \leq 0$ ，其中正确的结论是（）

A、①②③ B、①② C、③④ D、①②③④

查看试题解析

二、填空题

11. 把一个足球垂直地面向上踢，t（秒）后该足球的高度h（米）适用公式h=20t﹣5t² ．则经过秒时球的高度为15米．

查看试题解析
12. 如图，抛物线 $y = a x^{2}$ 与直线 $y = b x + c$ 的两个交点坐标分别为 $A (- 3, 9)$ ， $B (1, 1)$ ，则关于x的方程 $a x^{2} - b x - c = 0$ 的解为．

查看试题解析
13. 将二次函数 $y = - x^{2} + 2 x + 3$ 的图象在x轴上方的部分沿x轴翻折后，所得新函数的图象如图所示．当直线 $y = x + b$ 与新函数的图象恰有3个公共点时，b的值为

查看试题解析
14. 玥玥看到一处喷水景观，喷出的水柱呈抛物线形状，她对此展开研究：发现水柱距地面的高度 $y (m)$ 与水柱距喷水头的水平距离 $x (m)$ 之间近似满足函数关系 $y = - \frac{1}{10} {(x - h)}^{2} + k$ 的图象，已知水柱在距喷水头 $P$ 水平距离 $5 m$ 处达到最高，最高点距离地面 $3.2 m$ ．身高 $1.6 m$ 的玥玥站在水柱正下方，且距喷水头 $P$ 水平距离 $8 m$ 的位置，她的头顶碰到水柱．（填“能”或“不能”）

查看试题解析
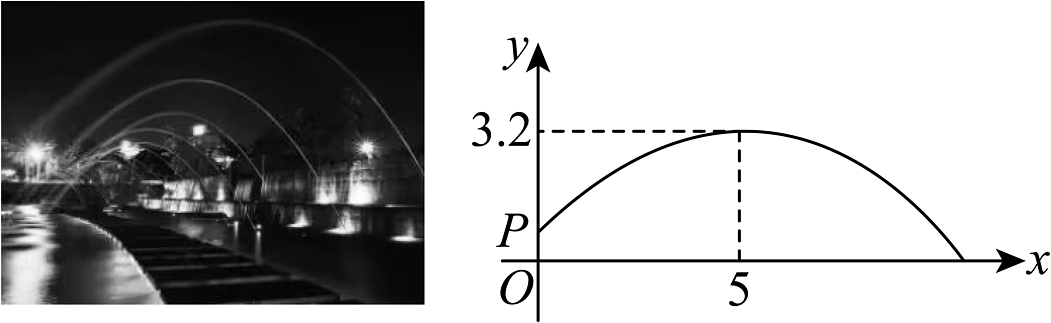15. 如图，已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图像，下列结论① $a b c > 0$ ；② $b^{2} > 4 a c$ ；③ $a (m^{2} - 1) + b (m - 1) < 0 (m \neq 1)$ ；④关于x的方程 $|a x^{2} + b x + c| = 1$ 有四个根，且这四个根的和为5；其中正确的结论有（请写出所有正确结论的序号）．

查看试题解析

三、解答题

16. 如图为二次函数 $y = - x^{2} - 2 x + 3$ 的图象，试观察图象回答下列问题：

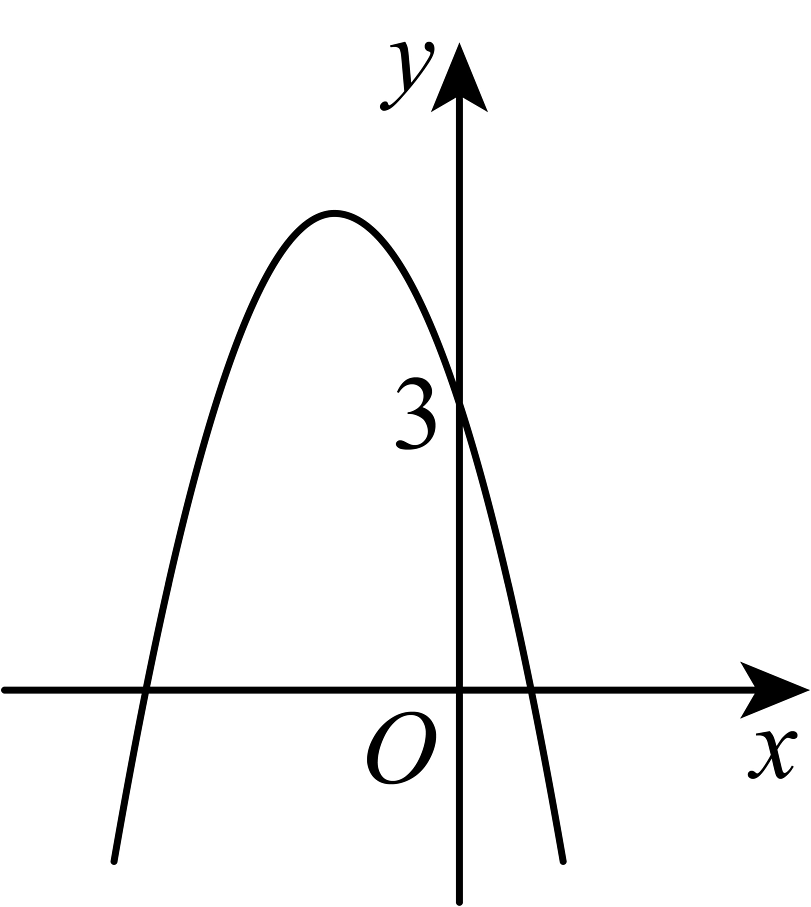(1)、写出方程 $- x^{2} - 2 x + 3 = 0$ 的解为 $x_{1} =$ ___________， $x_{2} =$ ___________；

(2)、当 $y > 0$ 时，直接写出 $x$ 的取值范围为___________；

(3)、当 $- 3 < x < 3$ 时，直接写出 $y$ 的取值范围是___________．

查看试题解析
17. 丁丁推铅球的出手高度为 $1.6 m$ ，在如图所示的直角坐标系中，铅球运动轨迹是抛物线 $y = - 0.1 (x - k)^{2} + 2.5$ ，求铅球的落点与丁丁的距离．

查看试题解析
18. 为了推进“绿美潮州”生态建设，潮州市某公司加快技术升级改造， $2023$ 年第一季度 $A$ 产品的生产成本是每件 $200$ 元，技术升级改造后， $A$ 产品的生产成本逐季度下降，第三季度 $A$ 产品的生产成本是每件 $128$ 元，若 $A$ 产品生产成本每个季度的平均下降率都相同．求该产品生产成本每个季度的平均下降率是多少．

查看试题解析
19. 已知二次函数 $y = 2 (x - 1) (x - m - 3)$ (m 为常数).

(1)、求证：不论 m 为何值，该函数的图象与 x 轴总有公共点；

(2)、当 m 取什么值时，该函数的图象与 y 轴的交点在 x 轴的上方？

查看试题解析
20. 已知二次函数 $y = x^{2} + b x + c$ （b，c为常数）的图象经过点 $A (- 2, 5)$ ，对称轴为直线 $x = - \frac{1}{2}$ ．

(1)、求二次函数的表达式；

(2)、若点 $B (1, 7)$ 向上平移2个单位长度，向左平移m（ $m > 0$ ）个单位长度后，恰好落在 $y = x^{2} + b x + c$ 的图象上，求m的值；

(3)、当 $- 2 \leq x \leq n$ 时，二次函数 $y = x^{2} + b x + c$ 的最大值与最小值的差为 $\frac{9}{4}$ ，求n的取值范围．

查看试题解析
21. 有这样一个问题：探究函数 $y = x^{2} - 4 |x| + 3$ 的图象与性质．
小丽根据学习函数的经验，对函数 $y = x^{2} - 4 |x| + 3$ 的图象与性质进行了探究．
下面是小丽的探究过程，请补充完整：

(1)、函数 $y = x^{2} - 4 |x| + 3$ 的自变量x的取值范围是 ________．

(2)、如图，在平面直角坐标系xOy中，画出了函数 $y = x^{2} - 4 |x| + 3$ 的部分图象，用描点法将这个函数的图象补充完整；

(3)、对于上面的函数 $y = x^{2} - 4 |x| + 3$ ，下列四个结论：
①函数图象关于y轴对称；
②函数既有最大值，也有最小值；
③当 $x \geq 2$ 时，y随x的增大而增大，当 $x \leq - 2$ 时，y随x的增大而减小；
④函数图象与x轴有2个公共点．
所有正确结论的序号是________．

(4)、结合函数图象，解决问题：
若关于x的方程 $x^{2} - 4 |x| + 3 = k$ 有4个不相等的实数根，则k的取值范围是________．

查看试题解析
22. 为了增加趣味性，万岁山旅游城把传统的抛绣球项目进行改良，他们定制了一种器械，类似中国古代一种投石器，为了解发射平台高度对绣球飞行轨迹的影响，我们可以设定不同的发射平台高度，并分别记录绣球在不同水平距离上的飞行高度. 分析不同发射平台高度下绣球的飞行轨迹. 通过比较不同高度下绣球的飞行高度和飞行距离，我们可以得出发射平台高度对绣球运动轨迹的具体影响. 从而有目的地调整发射高度，通过实验发现绣球运动轨迹是抛物线的一部分，并且在离发射点水平距离18米处达到距地面最大高度18米；在离发射点水平距离6米处，距地面高度10米.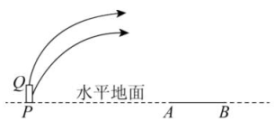
问题解决：

(1)、任务1：确定函数表达式. 设绣球离发射点水平距离为x，距地面高度为y. 求出y关于x的函数表达式；

(2)、任务2：探究飞行距离，当绣球从地面发出到落地（高度为0m）时，飞行的水平距离是多少；

(3)、任务3：如图，工作人员在水平地面上设置一个高度可以变化的发射平台PQ，当弹射口高度变化时，绣球被弹出后的飞行轨迹形状不变，可视为抛物线上下平移得到，点P、A、B在一条直线上，已知 $A P = 37 m$ ， $A B = 1 m$ ，游客小李站在线段AB（包括点A、B）上，为了确保他能抢到绣球，求发射台PQ的变化范围.

查看试题解析
23. 已知二次函数 $y_{1} = - x^{2} + b x + c (b, c$ 为常数 $)$ 图象的顶点横坐标比二次函数 $y_{2} = - x^{2} + 2 x + c$ 图象的顶点横坐标大 $1$ ．

(1)、求 $b$ 的值．

(2)、已知点 $A (x_{1}, m)$ 在二次函数 $y_{1} = - x^{2} + b x + c$ 的图象上，点 $B (x_{2}, n)$ 在二次函数 $y_{2} = - x^{2} + 2 x + c$ 的图象上．
$①$ 若 $x_{2} = 2 x_{1} + 1$ ，求 $n - m$ 的最大值．
$②$ 若 $x_{2} - x_{1} = t$ ，且 $x_{1} \geq 0$ 时，始终有 $n - m = 3 t$ ，求 $t$ 的值．

查看试题解析

x	…	-3	-2	-1	0	1	…
y	…	-1	-4	-1	8	23	…

2025年人教版数学九年级上册周测卷 （第二十二章 第2-3节）培优卷

一、选择题

二、填空题

三、解答题

2025年人教版数学九年级上册周测卷（第二十二章第2-3节）培优卷