第六章《一次函数》提升卷—鲁教版(五四制)数学七(上)单元测
试卷更新日期:2025-10-12 类型:单元试卷
一、选择题:本大题共10小题,每小题3分,在每小题给出的四个选项中,只有一个是正确的.每小题选对得3分,选错、不选或多选,均不得分.
-
1. 下列各关系中,符合正比例函数关系的是( ).A、正方形的周长p和它的一边长a B、距离s一定时,速度v和时间t C、圆的面积S和圆的半径r D、圆柱的体积V和底面半径r2. “儿子学成今日返,儿子已到父未到,父亲到后细端详,父子高兴把家还,”如图,用y轴表示父亲与儿子行进中离家的距离,用x轴表示父亲离家的时间,那么下列图象与上述诗的含义大致相吻合的是( )A、
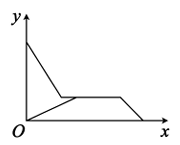 B、
B、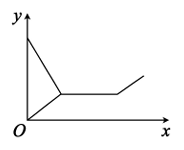 C、
C、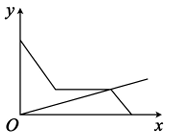 D、
D、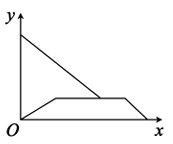 3. 某树苗原始高度为 , 如图是该树苗的高度与生长的月数的有关数据示意图,假设以后一段时间内,该树苗高度的变化与月数保持此关系,则它的高度(单位:)与生长月数之间的关系式为( )
3. 某树苗原始高度为 , 如图是该树苗的高度与生长的月数的有关数据示意图,假设以后一段时间内,该树苗高度的变化与月数保持此关系,则它的高度(单位:)与生长月数之间的关系式为( )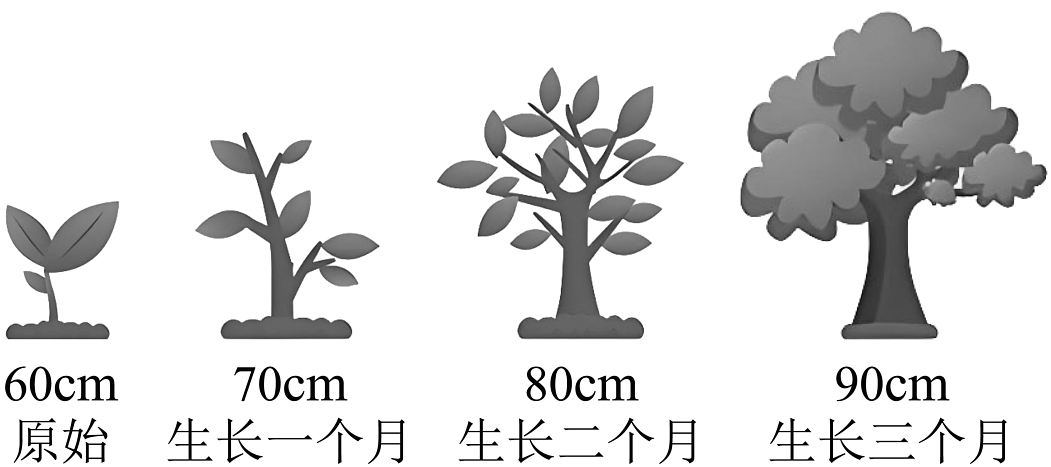 A、 B、 C、 D、4. 关于x的正比例函数与一次函数的大致图象不可能是( )A、
A、 B、 C、 D、4. 关于x的正比例函数与一次函数的大致图象不可能是( )A、 B、
B、 C、
C、 D、
D、 5. 在学习了用描点法画函数图象之后,小马同学对某个一次函数列表取对应值如下:
5. 在学习了用描点法画函数图象之后,小马同学对某个一次函数列表取对应值如下:x
…
-2
-1
0
1
2
…
y
…
-5
-3
-1
0
3
…
他在最后描点连线时发现有一个点明显不对,这个点是( ).
A、 B、 C、 D、6. 如图,在平面直角坐标系中,、两点在一次函数的图象上,其坐标分别为 , , 下列结论正确的是( ) A、 , B、 , C、 , D、7. 如图,在平面直角坐标系中有一个的正方形网格,其右下角格点(小正方形的顶点)的坐标为 , 左上角格点的坐标为 , 若分布在直线两侧的格点数相同,则的取值可以是( ).
A、 , B、 , C、 , D、7. 如图,在平面直角坐标系中有一个的正方形网格,其右下角格点(小正方形的顶点)的坐标为 , 左上角格点的坐标为 , 若分布在直线两侧的格点数相同,则的取值可以是( ). A、 B、 C、2 D、8. 关于函数 , 给出下列说法正确的是:( )
A、 B、 C、2 D、8. 关于函数 , 给出下列说法正确的是:( )①当时,该函数是一次函数;
②若点在该函数图象上,且 , 则;
③若该函数不经过第四象限,则;
④该函数恒过定点 .
A、①②④ B、①③④ C、②③④ D、①②③9. 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶时间为小时,两车之间距离为千米,图中的折线表示与之间的函数关系.若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇,则第二列快车比第一列快车晚出发( ) A、0.5小时 B、0.6小时 C、0.75小时 D、0.8小时10. 漏刻是我国古代的一种计时工具,据史书记载,西周时期就已经出现了漏刻,这是中国古代人民对函数思想的创造性应用。数学活动小组依据漏刻的原理制作了一个简单的漏刻计时工具模型,每2分钟记录一次箭尺读数,得到漏刻水位h(cm)与时间t(min)的实验数据如下表:
A、0.5小时 B、0.6小时 C、0.75小时 D、0.8小时10. 漏刻是我国古代的一种计时工具,据史书记载,西周时期就已经出现了漏刻,这是中国古代人民对函数思想的创造性应用。数学活动小组依据漏刻的原理制作了一个简单的漏刻计时工具模型,每2分钟记录一次箭尺读数,得到漏刻水位h(cm)与时间t(min)的实验数据如下表:数据记录
第1次
第2次
第3次
第4次
第5次
……
t(min)
0
2
4
6
8
……
h(cm)
2
2.8
3.6
4.2
5.2
……
下列说法错误的是( )
A、在实验开始时,漏刻水位是2cm B、第4次数据记录出现了错误,正确的漏刻水位应该是4.4cm C、第7次数据记录时,漏刻水位应为6.8cm D、当漏刻水位为10cm时,对应实验的时间是10min二、填空题:本大题共6小题,每小题3分,共18分.只要求填出最后结果.
-
11. 函数的自变量的取值范围是 .12. 已知是关于x的一次函数,则 .13. 如图,在中,点从点出发向点运动,在运动过程中,设表示线段的长,表示的面积,点到的距离为6,则与之间的关系式为: .
 14. 已知关于x,y的方程组的解为 , 则一次函数y=kx+3与y=2x+b的图象交点坐标为 .15. 如图,在平面直角坐标系中,直线:与直线:交于点 , 直线与轴交于点 , 直线:过点 , 点是横轴上任意一点,满足:是等腰三角形的点坐标是 .
14. 已知关于x,y的方程组的解为 , 则一次函数y=kx+3与y=2x+b的图象交点坐标为 .15. 如图,在平面直角坐标系中,直线:与直线:交于点 , 直线与轴交于点 , 直线:过点 , 点是横轴上任意一点,满足:是等腰三角形的点坐标是 .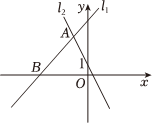 16. 如图,若正比例函数y=kx图象与四条直线x=﹣1,x=2,y=2,y=4相交围成的长方形ABCD有公共点,则k的取值范围是 .
16. 如图,若正比例函数y=kx图象与四条直线x=﹣1,x=2,y=2,y=4相交围成的长方形ABCD有公共点,则k的取值范围是 .
三、解答题:本大题共8小题,共72分.
-
17. 行驶中的汽车,在刹车后由于惯性的作用,还要继续向前滑行一段距离才能停止,这段距离称为“刹车距离”为了测定某种型号汽车的刹车性能车速不超过 , 对这种型号的汽车进行了测试,测得的数据如下表:
刹车时车速
刹车距离
(1)、当刹车时车速为时,刹车距离是;(2)、该种型号汽车的刹车距离用表示,刹车时车速用表示,根据上表反映的规律,直接写出与之间的关系式;(3)、该种车型的汽车在车速为的行驶过程中,司机至少和前面的汽车保持多远的距离,才能在紧急情况时急刹不会和前车追尾?18. 为提醒人们节约用水,及时修好漏水的水龙头,小明同学做了水龙头漏水实验,每隔10秒观察量筒中水的体积,记录的数据如表(漏出的水量精确到1毫升),已知用于接水的量筒最大容量为100毫升。时间t(秒)
10
20
30
40
50
60
70
量筒内水量v(毫升)
4
6
8
10
12
14
16
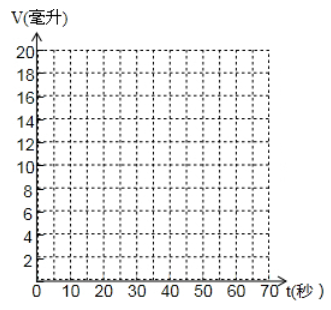 (1)、在图1的平面直角坐标系中,以(t;v)为坐标描出上表中数据对应的点;(2)、用光滑的曲线连接各点,并写出你猜测的ⅴ与t的函数关系式。(3)、解决问题:
(1)、在图1的平面直角坐标系中,以(t;v)为坐标描出上表中数据对应的点;(2)、用光滑的曲线连接各点,并写出你猜测的ⅴ与t的函数关系式。(3)、解决问题:①小明同学所用量筒开始实验前原有存水毫升;
②如果小明同学继续实验,当量筒中的水刚好盛满时所需时间是秒;
③按此漏水速度,半小时会漏水毫升。
19. 通过一次函数的学习,我们学会了列表、描点、连线的方法来画出函数图象并结合函数图象研究函数性质小明想应用这个方法来探究函数的性质下面是他的探究过程,请你补充完整: (1)、列表:
(1)、列表:直接填空: .
(2)、描点并画出该函数的图象.(3)、观察的图象,类比一次函数,请写出该函数的两条性质:;
.
(4)、在平面直角坐标系中,我们将横、纵坐标均为整数的点称为整点则该函数图象与直线围成的区域内不包括边界整点的个数为 .20. 如图,直线经过点和点 , 与x轴交于点C (1)、求k , m的值;(2)、求的面积;(3)、若点P在x轴上,当为等腰三角形时,直接写出此时点P的坐标21. 如图(1),在平面直角坐标系中,直线交坐标轴于A、B两点,过点作交于D , 交y轴于点E . 且 .
(1)、求k , m的值;(2)、求的面积;(3)、若点P在x轴上,当为等腰三角形时,直接写出此时点P的坐标21. 如图(1),在平面直角坐标系中,直线交坐标轴于A、B两点,过点作交于D , 交y轴于点E . 且 .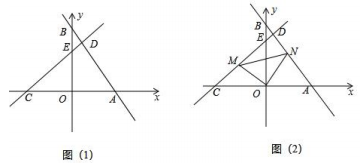 (1)、求B点坐标为;线段的长为;(2)、确定直线解析式,求出点D坐标;(3)、如图2,点M是线段上一动点(不与点C、E重合),交于点N , 连接 .
(1)、求B点坐标为;线段的长为;(2)、确定直线解析式,求出点D坐标;(3)、如图2,点M是线段上一动点(不与点C、E重合),交于点N , 连接 .①点M移动过程中,线段与数量关系是否不变,直接写出结论;
②当面积最小时,求点M的坐标和面积.
22. 图1是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上).现将甲槽的水匀速注入乙槽,甲、乙两个水槽中水的深度y(厘米)与注水时间x(分钟)之间的关系如图2所示. (1)、甲水槽中水的下降速度为 厘米/分钟,铁块高度为 厘米;(2)、求出注水第几分钟时,甲、乙水槽中水的深度相差1厘米?(3)、若甲槽底面积为56平方厘米,乙槽底面积为42平方厘米(壁厚不计),乙槽中铁块的体积多少立方厘米?23. 在平面直角坐标系中,直线为一、三象限角平分线,点关于轴的对称点称为的一次反射点,记作;关于直线的对称点称为点的二次反射点,记作 . 例如,点( , 5)的一次反射点为(2,5),二次反射点为(5,2).根据定义,回答下列问题:
(1)、甲水槽中水的下降速度为 厘米/分钟,铁块高度为 厘米;(2)、求出注水第几分钟时,甲、乙水槽中水的深度相差1厘米?(3)、若甲槽底面积为56平方厘米,乙槽底面积为42平方厘米(壁厚不计),乙槽中铁块的体积多少立方厘米?23. 在平面直角坐标系中,直线为一、三象限角平分线,点关于轴的对称点称为的一次反射点,记作;关于直线的对称点称为点的二次反射点,记作 . 例如,点( , 5)的一次反射点为(2,5),二次反射点为(5,2).根据定义,回答下列问题: (1)、点(3,4)的一次反射点为 , 二次反射点为;(2)、当点在第三象限时,点( , 1),N(3,),Q( , )中可以是点的二次反射点的是;(3)、若点A在第二象限,点 , 分别是点的一次、二次反射点, , 求射线与轴所夹锐角的度数;(4)、若点A在轴左侧,点 , 分别是点的一次、二次反射点,是等腰直角三角形,请直接写出点在平面直角坐标系中的位置.24. 综合与实践
(1)、点(3,4)的一次反射点为 , 二次反射点为;(2)、当点在第三象限时,点( , 1),N(3,),Q( , )中可以是点的二次反射点的是;(3)、若点A在第二象限,点 , 分别是点的一次、二次反射点, , 求射线与轴所夹锐角的度数;(4)、若点A在轴左侧,点 , 分别是点的一次、二次反射点,是等腰直角三角形,请直接写出点在平面直角坐标系中的位置.24. 综合与实践下表是两种“5G优惠套餐”计费方式.每月基本服务费固定收,通话时间不超时,上网流量不超量不再收费,通话时间超时(不足一分钟按一分钟计算)和上网超流量部分(不足1G按1G计算)加收超时通话费和超流量费.
套餐A
套餐B
服务项目
国内通话十上网流量
国内通话十上网流量
每月基本服务费
38元
58元
免费通话时间
100分钟
300分钟
超时通话每分钟收费
元
元
免费上网流量
8G
10G
套餐外流量
不足1G时按1G收费(5元/G),达到1G(即5元)时,再额外赠送1G免费流量,当免费流量用完后,仍按5元/G收费.
(1)、若小雨的妈妈某月通话时间为350分钟,上网流量为5G,则她的妈妈按套餐计费需付多少元,按套餐计费需付多少元;(2)、若小雨上网流量每月不超过8G,设通话时间为分钟 , 所需付出的费用为元,分别写出套餐、套餐中与之间的关系式;(3)、小雨通过几个月对账单发现,自己每月100分钟的通话时间绰绰有余,但上网流量波动比较大,设上网流量为(且为整数),那么小雨选择哪种套餐更优惠?