2025年人教版八年级上册周测卷 (第十四章 第1-2节)基础卷
试卷更新日期:2025-10-12 类型:复习试卷
一、选择题
-
1. 已知 , 若 , , , 则( )A、 B、 C、 D、无法确定2. 如图,用直尺和圆规作一个角等于已知角,能得出的依据是( )
 A、 B、 C、 D、3. 如图, , 若 , , 则( )
A、 B、 C、 D、3. 如图, , 若 , , 则( ) A、6 B、4 C、10 D、144. 如图,小筧家里有一块三角形玻璃碎了,他带着残缺的玻璃去玻璃店配一块与原来相同的,请问师傅配出相同玻璃的依据是( )
A、6 B、4 C、10 D、144. 如图,小筧家里有一块三角形玻璃碎了,他带着残缺的玻璃去玻璃店配一块与原来相同的,请问师傅配出相同玻璃的依据是( )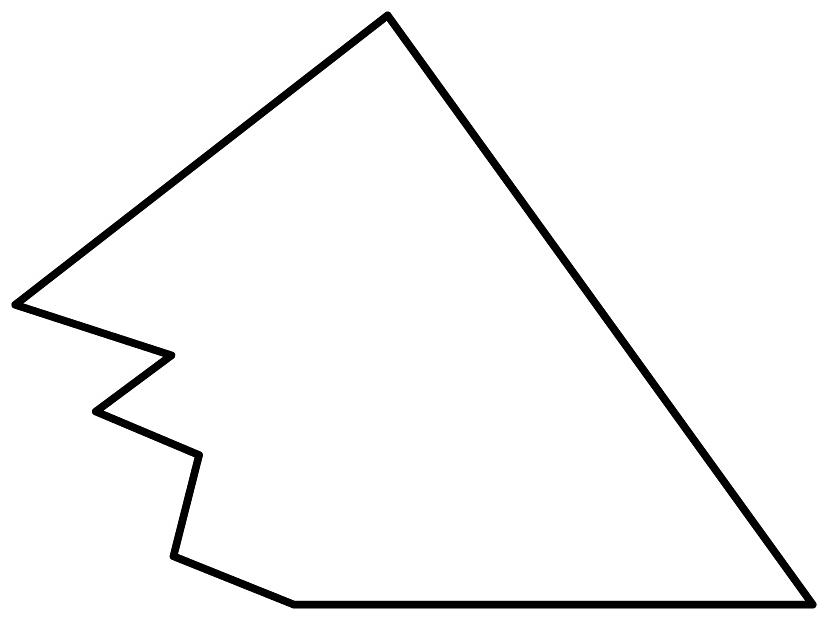 A、 B、 C、 D、5. 如图,用三角尺按如下方法画角平分线:在、上分别取点M、N,使 , 再分别过点M,N作、的垂线,交点为P,画射线 , 则平分 , 其作图原理是: , 这样就有 , 则这两个三角形全等的依据是( )
A、 B、 C、 D、5. 如图,用三角尺按如下方法画角平分线:在、上分别取点M、N,使 , 再分别过点M,N作、的垂线,交点为P,画射线 , 则平分 , 其作图原理是: , 这样就有 , 则这两个三角形全等的依据是( ) A、 B、 C、 D、6. 如图, , 若 , 则的长为( )
A、 B、 C、 D、6. 如图, , 若 , 则的长为( ) A、3 B、6 C、2 D、47. 如图,点B、D、E、C在同一直线上,△ABD≌△ACE,∠AEC=100°,则∠DAE=( )
A、3 B、6 C、2 D、47. 如图,点B、D、E、C在同一直线上,△ABD≌△ACE,∠AEC=100°,则∠DAE=( )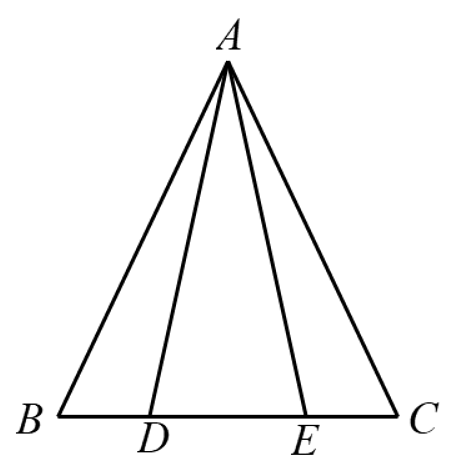 A、10° B、20° C、30° D、80°8. 如图,在的两边上截取 , . 连接 , 交于点 , 则下列结论正确的是
A、10° B、20° C、30° D、80°8. 如图,在的两边上截取 , . 连接 , 交于点 , 则下列结论正确的是①;②;③;④ .
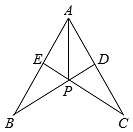 A、①②③④ B、①②③ C、②③④ D、①③④9. 如图,已知 , 平分 , 若 , , 则的度数是( )
A、①②③④ B、①②③ C、②③④ D、①③④9. 如图,已知 , 平分 , 若 , , 则的度数是( ) A、 B、 C、 D、10. 如图,、E是直线上不重合的两点,是的角平分线,于点A,若的周长为10,则的周长可能是( )
A、 B、 C、 D、10. 如图,、E是直线上不重合的两点,是的角平分线,于点A,若的周长为10,则的周长可能是( )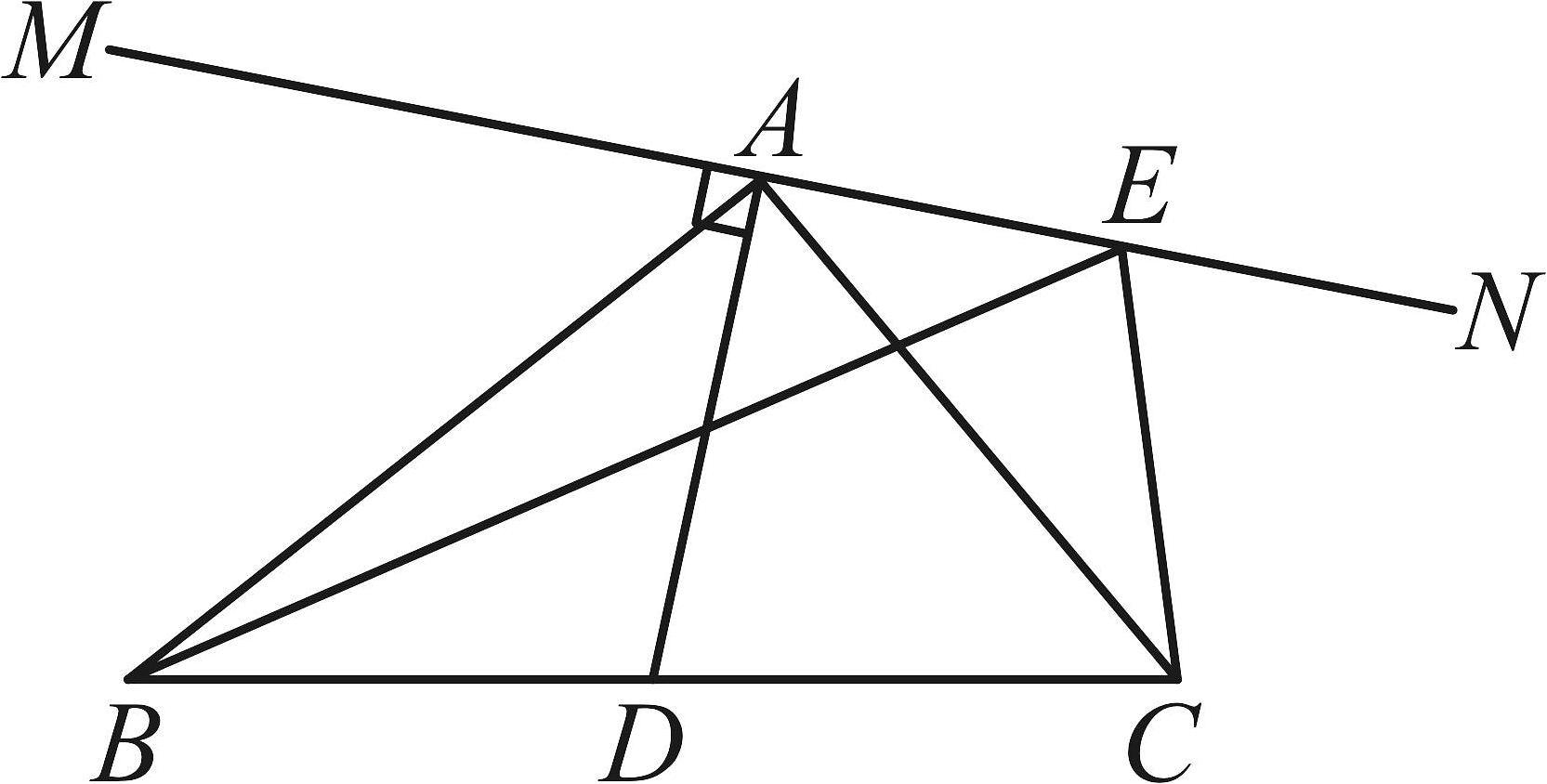 A、8 B、9 C、10 D、11
A、8 B、9 C、10 D、11二、填空题
-
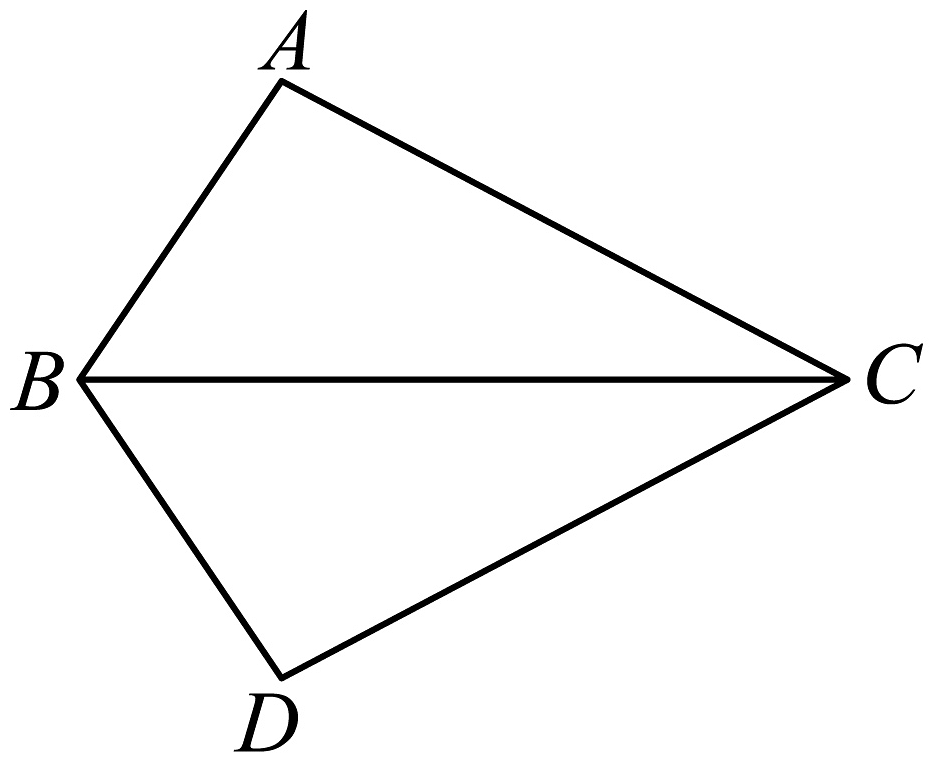
11. 如图,已知 , 那么 .
 12. 如图,已知 , , 请你只添加一个条件,使得 , 你添加的条件是 . (填序号)①;② .
12. 如图,已知 , , 请你只添加一个条件,使得 , 你添加的条件是 . (填序号)①;② .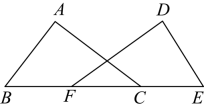 13. 为改善照明环境,小区物业在一号楼底部和二号楼顶部分别安装了照射灯(灯的高度忽略不计),如图,已知A处地面灯恰好照射到二号楼顶部灯B处,B灯恰好照射到一号楼顶部C处,且两盏灯的光线与地平面的夹角相等,若一号楼AC的高为44.8m,则二号楼BD的高为
13. 为改善照明环境,小区物业在一号楼底部和二号楼顶部分别安装了照射灯(灯的高度忽略不计),如图,已知A处地面灯恰好照射到二号楼顶部灯B处,B灯恰好照射到一号楼顶部C处,且两盏灯的光线与地平面的夹角相等,若一号楼AC的高为44.8m,则二号楼BD的高为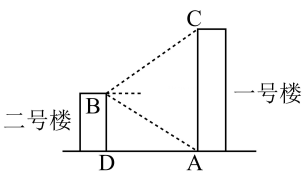 14. 如图,D在边上, , , 则的度数为 .
14. 如图,D在边上, , , 则的度数为 . 15. 如图,△ABC中,AD、BD、CD分别平分△ABC的外角∠CAE、内角∠ABC、外角∠ACF,AD∥BC.以下结论:①∠ABC=∠ACB;②∠ADC+∠ABD=90°;③BD平分∠ADC;④2∠BDC=∠BAC.其中正确的结论有 . (填序号)
15. 如图,△ABC中,AD、BD、CD分别平分△ABC的外角∠CAE、内角∠ABC、外角∠ACF,AD∥BC.以下结论:①∠ABC=∠ACB;②∠ADC+∠ABD=90°;③BD平分∠ADC;④2∠BDC=∠BAC.其中正确的结论有 . (填序号)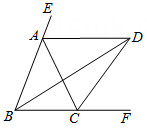
三、解答题
-
16. 如图,点B,F,C,E在同一条直线上, , , , , . 求线段的长和的度数.
 17. 如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A 和B. 连接并延长到点D,使 , 连接 并延长到点E,使 , 连接 , 那么量出的长就是A,B的距离.为什么?
17. 如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A 和B. 连接并延长到点D,使 , 连接 并延长到点E,使 , 连接 , 那么量出的长就是A,B的距离.为什么? 18. 沿着图中的虚线,用两种方法将下面的图形划分为两个全等的图形.
18. 沿着图中的虚线,用两种方法将下面的图形划分为两个全等的图形. 19. 如图,点分别在上, .
19. 如图,点分别在上, . (1)、求证:;(2)、若 , 求的度数.20. 【问题背景】等腰直角三角形是一种特殊的三角形;它的两条直角边长度相等,另外两个锐角相等,都为;在数学问题中,常常利用等腰直角三角形的特殊性质来求解角度、边长等问题.在工程设计中,等腰直角三角形的稳定性可以应用于一些结构的构建.例如某些特定的支撑架结构可能会利用等腰直角三角形的形状来保证稳定性.
(1)、求证:;(2)、若 , 求的度数.20. 【问题背景】等腰直角三角形是一种特殊的三角形;它的两条直角边长度相等,另外两个锐角相等,都为;在数学问题中,常常利用等腰直角三角形的特殊性质来求解角度、边长等问题.在工程设计中,等腰直角三角形的稳定性可以应用于一些结构的构建.例如某些特定的支撑架结构可能会利用等腰直角三角形的形状来保证稳定性.【问题解决】小明将一个等腰直角三角板的直角顶点放置在轴上;点、点分别是轴、轴上两个动点,直角边交轴于点 , 斜边交轴于点 .
 (1)、如图(1),已知点的横坐标为 , 直接写出点的坐标;(2)、如图(2),当等腰运动到使点恰为中点时,连接 ,
(1)、如图(1),已知点的横坐标为 , 直接写出点的坐标;(2)、如图(2),当等腰运动到使点恰为中点时,连接 ,求证: .
21. 如图,小明和小华家中间隔了一个办公楼,他们想要测量这个办公楼的高于于 . 小明在自家阳台处测得办公楼顶部的视线与水平线的夹角 , 小华在自家阳台处测得办公楼顶部的视线与水平线的夹角 . 已知三点共线,与互余,且 , 求办公楼的高度 .

