第五章《位置与坐标》提升卷—鲁教版(五四制)数学七(上)单元测
试卷更新日期:2025-10-12 类型:单元试卷
一、选择题:本大题共10小题,每小题3分,在每小题给出的四个选项中,只有一个是正确的.每小题选对得3分,选错、不选或多选,均不得分.
-
1. 有一张方格纸,每个小方格的边长是厘米,上面堆叠有棱长厘米的小正方体如图 , 小正方体的位置用表示,小正方体的位置用表示,那么小正方体的位置可以表示成( )
 A、 B、 C、 D、无正确选项2. 五子棋和象棋、围棋一样,深受同学们的喜爱,其规则:在正方形棋盘中,由黑方先行,轮流弈子,在任一方向上连成五子者为胜.如图是两个五子棋爱好者甲和乙的对弈图(甲执黑子先行,乙执白子后行).观察棋盘,若点M的位置记为(8,4),为了不让乙在短时间内获胜,甲必须将棋子落在( )
A、 B、 C、 D、无正确选项2. 五子棋和象棋、围棋一样,深受同学们的喜爱,其规则:在正方形棋盘中,由黑方先行,轮流弈子,在任一方向上连成五子者为胜.如图是两个五子棋爱好者甲和乙的对弈图(甲执黑子先行,乙执白子后行).观察棋盘,若点M的位置记为(8,4),为了不让乙在短时间内获胜,甲必须将棋子落在( ) A、(4,3)处 B、(3,5)处 C、(1,7)处或(5,3)处 D、(7,1)处3. 如图是一片枫叶标本,其形状呈“掌状五裂型”,裂片具有少数突出的齿.将其放在平面直角坐标系中,叶片“顶部”两点的坐标分别为 , 则叶杆“底部”点的坐标为( )
A、(4,3)处 B、(3,5)处 C、(1,7)处或(5,3)处 D、(7,1)处3. 如图是一片枫叶标本,其形状呈“掌状五裂型”,裂片具有少数突出的齿.将其放在平面直角坐标系中,叶片“顶部”两点的坐标分别为 , 则叶杆“底部”点的坐标为( ) A、 B、 C、 D、4. 年巴黎奥运会见证了中国体育代表团创造夏奥会境外参赛最佳战绩.如图所示是巴黎部分景点的平面示意图,每个小正方形的边长表示个单位长度,如果将凯旋门的位置记作 , 卢浮宫的位置记作 , 那么埃菲尔铁塔的位置是( )
A、 B、 C、 D、4. 年巴黎奥运会见证了中国体育代表团创造夏奥会境外参赛最佳战绩.如图所示是巴黎部分景点的平面示意图,每个小正方形的边长表示个单位长度,如果将凯旋门的位置记作 , 卢浮宫的位置记作 , 那么埃菲尔铁塔的位置是( )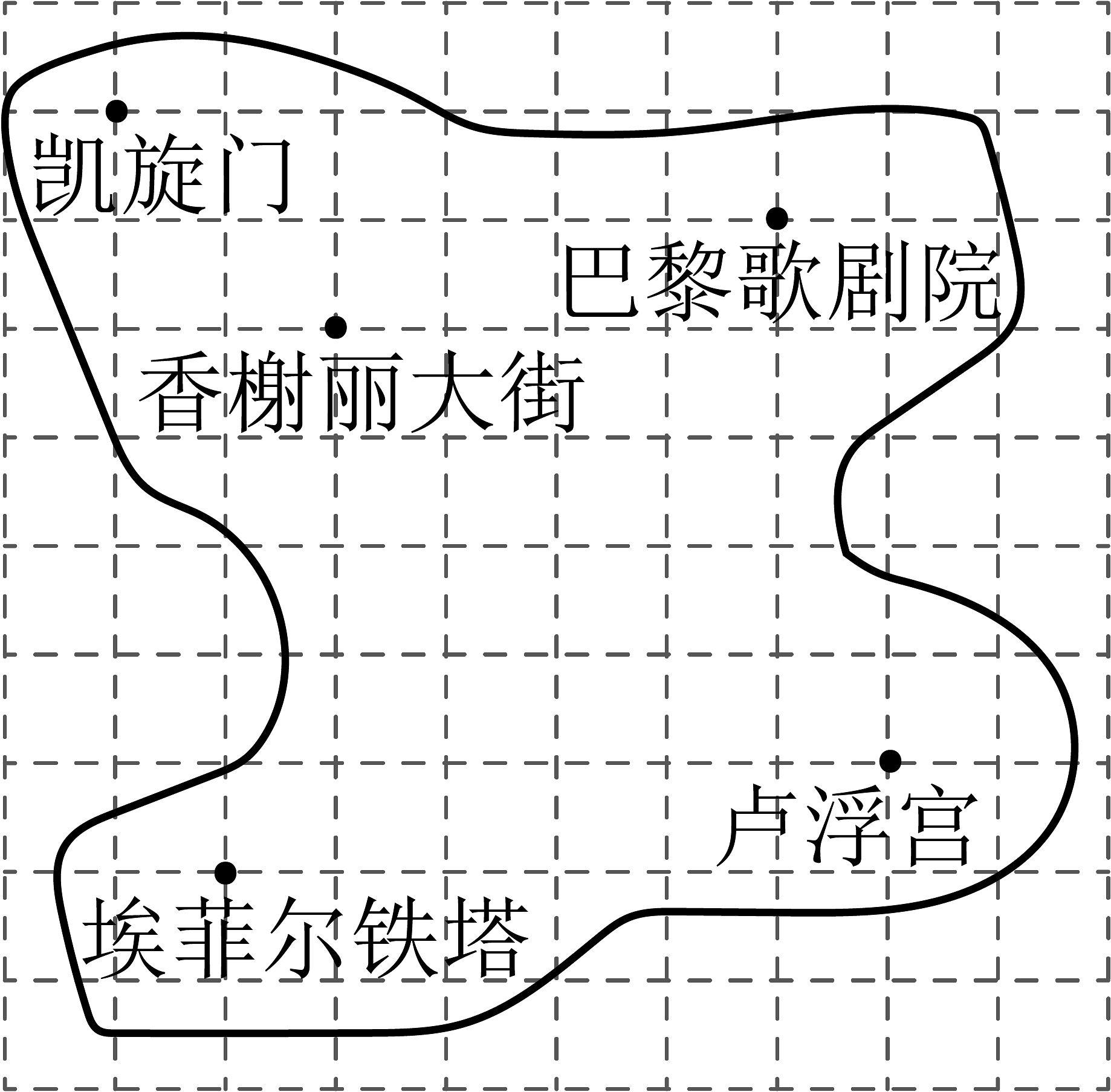 A、 B、 C、 D、5. 如图,一个粒子在第一象限内及x轴、y轴上运动,第一分钟,它从原点运动到点(1,0),第二分钟,它从点(1,0)运动到点(1,1),而后接着按图中箭头所示在与x轴、y轴平行的方向上来回运动,且每分钟移动1个单位长度,那么在第2 022分钟时,这个粒子所在位置的坐标是( )
A、 B、 C、 D、5. 如图,一个粒子在第一象限内及x轴、y轴上运动,第一分钟,它从原点运动到点(1,0),第二分钟,它从点(1,0)运动到点(1,1),而后接着按图中箭头所示在与x轴、y轴平行的方向上来回运动,且每分钟移动1个单位长度,那么在第2 022分钟时,这个粒子所在位置的坐标是( )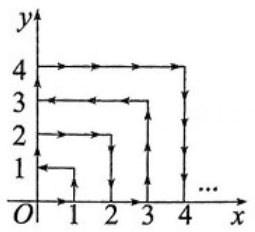 A、(44,4) B、(44,3) C、(44,2) D、(44,1)6. 在平面直角坐标系中,若点在第四象限,则点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 在平面直角坐标系中,第四象限内的点到轴的距离是3,到轴的距离是2,已知平行于轴且 , 则点的坐标是( )A、 B、 C、或 D、或8. 在平面直角坐标系中,已知点 A(3,-3),P是y 轴上一点,则使△AOP 为等腰三角形的点 P 共有( )个.A、2 B、3 C、4 D、59. 下列说法不正确的是( )A、点一定在第四象限 B、点到轴的距离为6 C、若中 , 则点在轴上 D、若 , 则点一定在第一,第三象限的角平分线上10. 如图,长方形纸片的边在轴上,且过原点,连结将纸片沿折叠,使点恰好落在边上的点处若 , 则点的纵坐标为( )
A、(44,4) B、(44,3) C、(44,2) D、(44,1)6. 在平面直角坐标系中,若点在第四象限,则点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 在平面直角坐标系中,第四象限内的点到轴的距离是3,到轴的距离是2,已知平行于轴且 , 则点的坐标是( )A、 B、 C、或 D、或8. 在平面直角坐标系中,已知点 A(3,-3),P是y 轴上一点,则使△AOP 为等腰三角形的点 P 共有( )个.A、2 B、3 C、4 D、59. 下列说法不正确的是( )A、点一定在第四象限 B、点到轴的距离为6 C、若中 , 则点在轴上 D、若 , 则点一定在第一,第三象限的角平分线上10. 如图,长方形纸片的边在轴上,且过原点,连结将纸片沿折叠,使点恰好落在边上的点处若 , 则点的纵坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本大题共6小题,每小题3分,共18分.只要求填出最后结果.
-
11. 已知直线 轴,点M的坐标为(1,2),并且线段 , 则点N的坐.标为.12. 如图,方格图中一个小正方形的对角线长10m,则点(0,0)东偏北45°方向30m处是点(3,3):点(4,2)南偏西45°方向20m处是点;
 13. 如图,在平面直角坐标系中,已知 , , 过点B作y轴的垂线l,P为直线l上一动点,连接 , , 则的最小值为 .
13. 如图,在平面直角坐标系中,已知 , , 过点B作y轴的垂线l,P为直线l上一动点,连接 , , 则的最小值为 .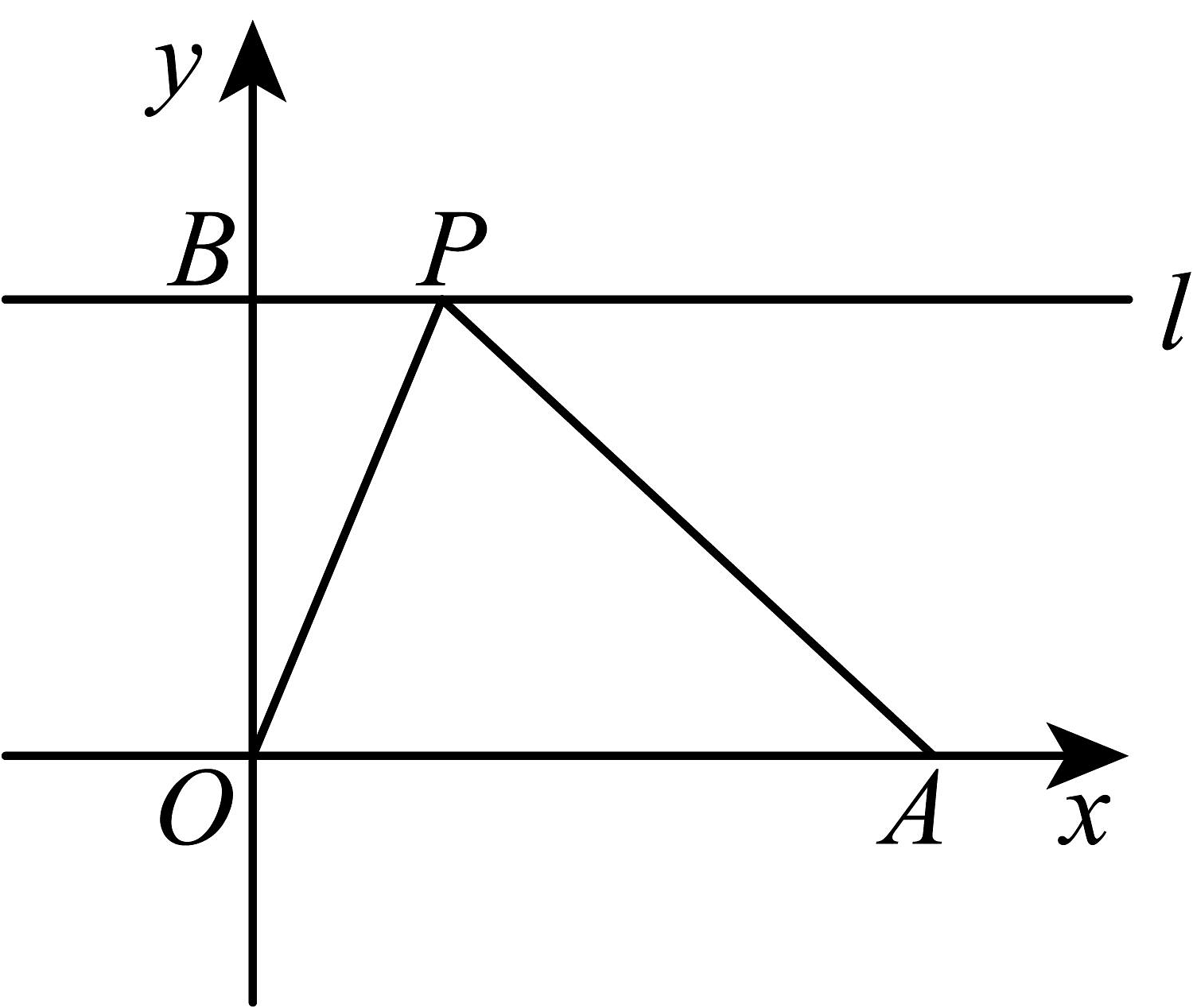 14. 如图①,某广场地面是用A,B,C三种类型的地砖平铺而成的.三种类型地砖的上表面图案如图②所示.现用有序数对表示每一块地砖的位置:第一行的第一块(A型)地砖记为(1,1),第二块( B型)地砖记为(2,1),……,若(m,n)位置恰好为A型地砖,则正整数m,n须满足的条件是
14. 如图①,某广场地面是用A,B,C三种类型的地砖平铺而成的.三种类型地砖的上表面图案如图②所示.现用有序数对表示每一块地砖的位置:第一行的第一块(A型)地砖记为(1,1),第二块( B型)地砖记为(2,1),……,若(m,n)位置恰好为A型地砖,则正整数m,n须满足的条件是 15. 在平面直角坐标系中,有一系列的点 , , , , , , 其中每一个点的横坐标是它前一个点的纵坐标的相反数与1的和,纵坐标是它前一个点的横坐标与2的和,即若点 , 则 , 若点 的坐标为 (2, 0),则点 的坐标为.16. 在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫作整点.已知点A(0,4),点B是x轴正半轴上的整点.记△AOB 内部(不包括边界)的整点个数为m,当m=3时,点B 的横坐标的所有可能值是;当点 B 的横坐标为4n(n为正整数)时,m=(用含 n 的代数式表示).
15. 在平面直角坐标系中,有一系列的点 , , , , , , 其中每一个点的横坐标是它前一个点的纵坐标的相反数与1的和,纵坐标是它前一个点的横坐标与2的和,即若点 , 则 , 若点 的坐标为 (2, 0),则点 的坐标为.16. 在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫作整点.已知点A(0,4),点B是x轴正半轴上的整点.记△AOB 内部(不包括边界)的整点个数为m,当m=3时,点B 的横坐标的所有可能值是;当点 B 的横坐标为4n(n为正整数)时,m=(用含 n 的代数式表示).
三、解答题:本大题共8小题,共72分.
-
17. 如图所示,点A表示3街与5大道的十字路口,点B表示5街与3大道的十字路口,如果用(3,5)→(4,5)→(5,5)→(5,4)→(5,3)表示由A到B的一条路径,那么你能用同样的方法写出由A到B的其他几条路径吗?请至少给出3种不同的路径.
 18. 如图1,将射线OX按逆时针方向旋转度,得到射线OY,如果点为射线OY上的一点,且 , 那么我们规定用表示点在平面内的位置,并记为 , .例如,图2中,如果 , 那么点在平面内的位置记为 , 根据图形,解答下面的问题.
18. 如图1,将射线OX按逆时针方向旋转度,得到射线OY,如果点为射线OY上的一点,且 , 那么我们规定用表示点在平面内的位置,并记为 , .例如,图2中,如果 , 那么点在平面内的位置记为 , 根据图形,解答下面的问题. (1)、如图3,如果点在平面内的位置记为 , 那么 , .(2)、如果点A,B在平面内的位置分别记为 , 试求A,B两点之间的距离并画出图形.19. 如图,在直角坐标系中,△ABC各顶点坐标分别为A(-3,3),B(-2,0),C(-1,1),△A'B'C'与△ABC 关于y轴对称,点A的对称点为A'。
(1)、如图3,如果点在平面内的位置记为 , 那么 , .(2)、如果点A,B在平面内的位置分别记为 , 试求A,B两点之间的距离并画出图形.19. 如图,在直角坐标系中,△ABC各顶点坐标分别为A(-3,3),B(-2,0),C(-1,1),△A'B'C'与△ABC 关于y轴对称,点A的对称点为A'。 (1)、作出ΔA'B'C';(2)、写出A'的坐标;(3)、若P为x轴上一动点,当CP+A'P最小时,直接写出点P的坐标。20. 在平面直角坐标中,已知点在第四象限.(1)、若已知的算术平方根是4,的立方根是 , c是的整数部分.试判断通过计算得到的点M是否满足题意,并说明理由;(2)、若 , 请结合画图判断点所在位置的区域,并说明理由.21. 在平面直角坐标系中,给出如下定义:点P到x轴、y轴的距离的较大值称为点P的“长距”,点Q到x轴、y轴的距离相等时,称点Q为“角平分线点”.(1)、点的“长距”为______;(2)、若点是“角平分线点”,求a的值;(3)、若点的长距为4,且点C在第二象限内,点D的坐标为 , 请判断点D是否为“角平分线点”,并说明理由.22. 如图,在平面直角坐标系中,点在轴的正半轴上,点的坐标为 , 线段轴.动点从点出发,沿方向运动;同时,动点从原点出发,沿轴向右运动,动点 , 的运动速度均为1个单位长度/秒.当点到达终点时,点也随之停止运动.连接 , 过的中点作垂直于的线段 , 点在右侧且 , 如图①.设运动时间为秒.
(1)、作出ΔA'B'C';(2)、写出A'的坐标;(3)、若P为x轴上一动点,当CP+A'P最小时,直接写出点P的坐标。20. 在平面直角坐标中,已知点在第四象限.(1)、若已知的算术平方根是4,的立方根是 , c是的整数部分.试判断通过计算得到的点M是否满足题意,并说明理由;(2)、若 , 请结合画图判断点所在位置的区域,并说明理由.21. 在平面直角坐标系中,给出如下定义:点P到x轴、y轴的距离的较大值称为点P的“长距”,点Q到x轴、y轴的距离相等时,称点Q为“角平分线点”.(1)、点的“长距”为______;(2)、若点是“角平分线点”,求a的值;(3)、若点的长距为4,且点C在第二象限内,点D的坐标为 , 请判断点D是否为“角平分线点”,并说明理由.22. 如图,在平面直角坐标系中,点在轴的正半轴上,点的坐标为 , 线段轴.动点从点出发,沿方向运动;同时,动点从原点出发,沿轴向右运动,动点 , 的运动速度均为1个单位长度/秒.当点到达终点时,点也随之停止运动.连接 , 过的中点作垂直于的线段 , 点在右侧且 , 如图①.设运动时间为秒. (1)、当时,点的坐标为___________;点的坐标为___________;(2)、当点落在轴上时,求的值;(3)、如图②,连接 , , 探究的面积是否为定值?若是,请求出该定值;若不是,请说明理由.23.
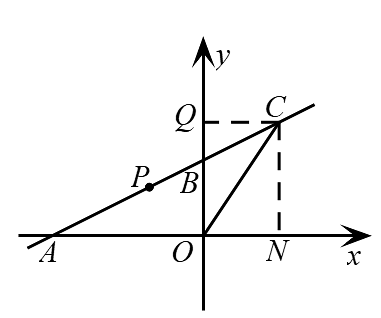
(1)、当时,点的坐标为___________;点的坐标为___________;(2)、当点落在轴上时,求的值;(3)、如图②,连接 , , 探究的面积是否为定值?若是,请求出该定值;若不是,请说明理由.23.如图,在平面直角坐标系中,直线与坐标轴交于 , , , 两点,点 , , , 在直线上.我们可以用面积法求点的坐标.
[问题探究]:
(1)请阅读并填空:一方面,过点作轴于点 , 我们可以由 , 的坐标,直接得出三角形 的面积为 平方单位;另一方面,过点作 轴于点 , 三角形 的面积 , 三角形的面积 平方单位.
三角形的面积三角形的面积三角形的面积,
可得关于的一元一次方程为
解这个方程,可得点的坐标为
[问题迁移]:
(2)请你仿照(1)中的方法,求点的纵坐标.[问题拓展]:
(3)若点 , 在直线上,且三角形的面积等于平方单位,请直接写出点的坐标.24. 我们学习了平移、旋转、轴对称等图形变换,这些图形变换不仅可以应用到精美的图案设计上,还可以解决生活实际问题. (1)、【图案设计】
(1)、【图案设计】如图1,在平面直角坐标系中, , , .
作出关于轴的对称图形 , 并标注出点 , , ;
(2)、【拓展应用】如图1,点是轴上一动点,并且满足的值最小,请在图中找出点的位置(保留作图痕迹),并直接写出的最小值为.
(3)、【实际应用】如图2,某地有一块三角形空地 , 已知 , 是内一点,连接后测得米,现当地政府欲在三角形空地中修一个三角形花坛 , 点 , 分别是 , 边上的任意一点(不与各边顶点重合),请问的周长最少约多少米?(保留整数)( , )