第四章《实数》提升卷—鲁教版（五四制）数学七（上）单元测

试卷更新日期：2025-10-12 类型：单元试卷

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，在每小题给出的四个选项中，只有一个是正确的.每小题选对得3分，选错、不选或多选，均不得分.

1. 在0， $\frac{2}{3}$ ， $- \sqrt{2}$ ， $\frac{π}{2}$ ， $\sqrt[3]{8}$ ， 0.101101110…(每两个“0”之间依次多一个“1”)中，无理数的个数是 ( )

A、2 B、3 C、4 D、5

查看试题解析
2. 有一个计算器，计算 $\sqrt{3}$ 时屏幕显示的结果为1.7320508，从左往右数只有九位（包括小数点），现在想知道第十位的数字是什么，可以在这个计算器中计算下面哪一个式子的值（）

A、 $10 \sqrt{3}$ B、 $10 (\sqrt{3} - 1)$ C、 $100 \sqrt{3}$ D、 $\sqrt{3} - 1$

查看试题解析
3. 若a，b是有理数，且a>0，b>0，则 ( )

A、a+b可以是无理数 B、a-b一定是负数 C、a÷b一定是有理数 D、 $\sqrt{a b}$ 一定是无理数

查看试题解析
4. 关于 $\sqrt[3]{6}$ ，下列说法不正确的是（）

A、它是一个无理数 B、它可以用数轴上的一个点来表示 C、它可以表示体积为6的正方体的棱长 D、若 $n < \sqrt[3]{6} < n + 1$ ，则 $n = 2$

查看试题解析
5. 按下图所示的运算程序，能使输出的结果为5的是（）

A、a=0，b=5 B、a=9，b=4 C、a=16，b=1 D、a=36，b= 1

查看试题解析
6. 若实数a，b满足 $a + b = 6$ ，我们就说a与b是关于6的“如意数”，则与 $3 - \sqrt{2}$ 是关于6的“如意数”是（）

A、 $3 + \sqrt{2}$ B、 $3 - \sqrt{2}$ C、 $9 - \sqrt{2}$ D、 $9 + \sqrt{2}$

查看试题解析
7. 下列说法不正确的是（）

A、0.04 的平方根是土0.2 B、-4是16的一个平方根 C、9的立方根是3 D、- $\sqrt[3]{- 27}$ =3

查看试题解析
8. 面积为8的正方形的边长为 $a$ ，则 $a$ 的大致范围是（）

A、1和2之间 B、2和3之间 C、3和4之间 D、大于4

查看试题解析
9. 设 $a = \sqrt{{(- \frac{1}{3})}^{2}}$ ， $b = {(- 2)}^{2}$ ， $c = \sqrt[3]{- 27}$ ， $d = - |- 2|$ ，则 $a, b, c, d$ 按由小到大顺序的排列为：（）

A、 $c < d < a < b$ B、 $d < c < a < b$ C、 $d < a < c < b$ D、 $c < a < d < b$

查看试题解析
10. 如图，把两个边长为2的小正方形分别沿对角线剪开，将四个直角三角形拼成一个大的正方形，则这个大正方形的边长为（）

A、 $\sqrt{2}$ B、4 C、 $\sqrt{8}$ D、8

查看试题解析

二、填空题：本大题共6小题，每小题3分，共18分.只要求填出最后结果.

11. 利用课本上的计算器进行计算，其按键顺序如下：，则显示结果为．

查看试题解析
12. 已知 $\sqrt{2} = 1.414$ ， $\sqrt{20} = 4.472$ ，那么 $\sqrt{200} =$ .

查看试题解析
13. 有一个数值转换器，原理如图所示，当输入的 $x = 256$ 时，输出的 $y$ 值是．

查看试题解析
14. 若点A在数轴上的位置如图所示，则点A在数轴上表示的无理数可能是．（只填一个）

查看试题解析
15. 物体自由下落的高度h（单位：米）与下落时间t（单位：秒）的关系是 $h = 4.9 t^{2}$ ．有一物体从 $122.5$ 米高的建筑物上自由落下，到达地面需要的时间为秒．

查看试题解析
16. 有下列说法：①无理数就是开方开不尽的数；②满足· $- \sqrt{2} < x < \sqrt{5}$ 的整数x有4个；③-3是 $\sqrt{81}$ 的一个平方根；④不带根号的数都是有理数；⑤不是有限小数的不是有理数；⑥对于任意实数a，都有 $\sqrt{a^{2}} = a .$ 其中正确的说法有.(填序号)

查看试题解析

三、解答题：本大题共8小题，共72分.

17. 判定下列各数，并把下列各数前面的序号写入相应的集合中：
① $- 12 %$ ② $|- \sqrt{9}|$ ③ $- \frac{π}{3}$ ④ $\sqrt[3]{16}$ ⑤0 ⑥ $- \frac{22}{7}$ ⑦ $- 2^{2}$
正实数集合{_____________________________________________…}；
无理数集合{_____________________________________________…}；
整数集合{_______________________________________________…}；
分数集合{_______________________________________________…}．

查看试题解析
18. 计算：

(1)、 $|- 2| + \sqrt[3]{- 27} - \sqrt{49} + {(- 1)}^{2}$ ；

(2)、 $\sqrt{{(- 2)}^{2}} - \sqrt[3]{8} + \sqrt[3]{- \frac{1}{27}}$ ．

查看试题解析
19. 在学习《实数》这一章时，我们利用“逐步逼近”的方法可以计算出 $\sqrt{2}$ 的近似值，得出 $1.4 < \sqrt{2} < 1.5 .$ 利用“逐步逼近”法，请回答下列问题：

(1)、若 $m < \sqrt{15} < n (m,$ n精确到0.1，且m，n是连续的一位小数)，则 $m =_{.}$ .

(2)、若a是 $\sqrt{15} + \sqrt{2}$ 的小数部分，b是 $\sqrt{15} - \sqrt{2}$ 的整数部分.
$① a =_{,} b =_{;}$
②求 ${(a - \sqrt{15} - \sqrt{2})}^{b}$ 的平方根.

查看试题解析
20. 教材上有这样一个合作学习活动：如图 $1$ ，依次连结 $2 \times 2$ 方格四条边的中点 $A$ ， $B$ ， $C$ ， $D$ ，得到一个阴影正方形，设每一小方格的边长为 $1$ ，得到阴影正方形面积为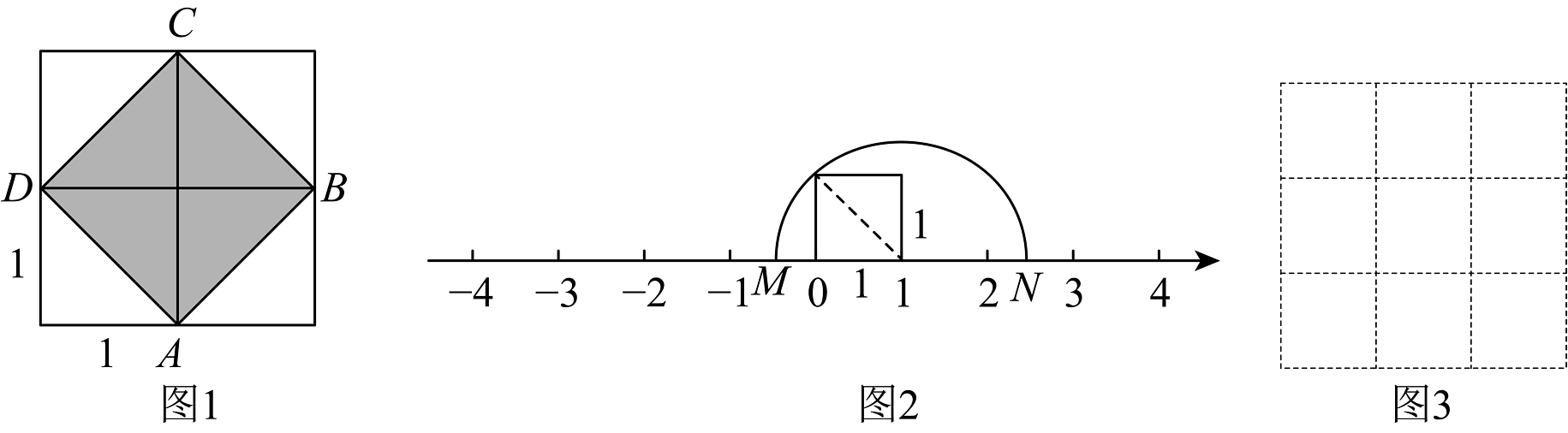 $2$ ：

(1)、发现图 $1$ 这个阴影正方形的边长就是小方格的对角线长，则小方格对角线长是_______，由此我们得到一种在数轴上找到无理数的方法；

(2)、如图 $2$ ，以 $1$ 个单位长度为边长画一个正方形，以数字 $1$ 所在的点为圆心，正方形的对角线为半径画弧，与数轴交于 $M$ ， $N$ 两点，则点 $M$ 表示的数为_______；

(3)、如图 $3$ ， $3 \times 3$ 网格是由 $9$ 个边长为 $1$ 的小方格组成，画出面积是 $5$ 的正方形，使它的顶点在网格的格点上．

查看试题解析
21. 天气晴朗时，一个人能看到大海的最远距离s（单位：千米）可用公式 $s^{2} = \frac{125}{8} ℎ$ 来估计，其中h（单位：米）是眼睛离海平面的高度．

(1)、如果小天站在岸边观察，当眼睛离海平面的高度是1.6米时，能看到多远？

(2)、若小天登上岸边的一个观望台A ，已知小天眼睛离观望台地面的高度是1.6米，他想看到距离岸边大约10千米处的一个货轮B ，则观望台至少离海平面高多少米才可以看得见？

查看试题解析
22. 阅读材料，完成下列任务：
【材料一】 $∵ 4 < 6 < 9$ ， $∴ \sqrt{4} < \sqrt{6} < \sqrt{9}$ ，即 $2 < \sqrt{6} < 3$ ， $∴ \sqrt{6}$ 的整数部分为 2，小数部分为 $\sqrt{6} - 2$ .
【材料二】若正方形面积为 105，则它的边长为 $\sqrt{105}$ . 我们可以按照以下方法求得 $\sqrt{105}$ 近似值：
$∵ 100 < 105 < 121$ ， $∴ \sqrt{100} < \sqrt{105} < \sqrt{121}$ ，即 $10 < \sqrt{105} < 11$ ，
$∴$ 设 $\sqrt{105} = 10 + x$ ，其中 $0 < x < 1$ ，
如图 1，画出边长为 $10 + x$ 的正方形，根据图中面积，得 $1 0^{2} + 2 \times 10 x + x^{2} = 105$ ，
$∵ x^{2}$ 较小，
$∴$ 忽略 $x^{2}$ ，得： $1 0^{2} + 2 \times 10 x \approx 105$ ，解得 $x \approx 0.25$ ， $∴ \sqrt{105} = 10 + x \approx 10.25$ .
【探究问题】

(1)、利用材料一中的方法， $\sqrt{31}$ 的整数部分是，小数部分是；

(2)、利用材料二中的方法，探究 $\sqrt{149}$ 的近似值（要求写出求解过程，结果精确到 0.01）；

(3)、【思维拓展】
a是 $\sqrt{17} - 1$ 的小数部分，b是 $6 - \sqrt{17}$ 的小数部分，则 $(a + b)^{2025}$ 的值是多少？

(4)、探究 $\sqrt{223}$ 的近似值，直接写出结果： $\sqrt{223} \approx$ （结果精确到 0.01）

查看试题解析
23. 魔方又叫鲁比克方块，与华容道、独立钻石棋一同被称为智力游戏界的三大不可思议、如图（1）是一个4阶魔方，由四层完全相同的64个小正方体组成，体积为 ${64cm}^{3}$ ．

(1)、求组成这个4阶魔方的小正方体的棱长．

(2)、若图（1）中的四边形 $A B C D$ 是一个正方形，求该正方形的面积及边长．

(3)、若把图（1）中正方形 $A B C D$ 放在数轴上，如图（2），使得点A与表示1的点重合，那么点D在数轴上表示的数为________，这个数的绝对值是．

查看试题解析

24. 跟华罗庚学猜数：

据说，我国著名数学家华罗庚在一次出国访问途中，看到飞机上邻座的乘客阅读的杂志上有一道智力题：一个数是59319，希望求它的立方根．华罗庚脱口而出：39．邻座的乘客十分惊奇，忙问计算的奥妙．

你知道华罗庚是怎样迅速准确地计算出来的吗？请按照下面的问题试一试：

①∵ $\sqrt[3]{1000} = 10$ ， $\sqrt[3]{1000000} = 100$ ，又∵ $1000 < 59319 < 1000000$ ，

∴ $10 < \sqrt[3]{59319} < 100$ ， ∴能确定59319的立方根是个两位数．

②59319的个位数是9，又∵ $9^{3} = 729$ ， ∴能确定59319的立方根的个位数是9．

③如果划去59319后面的三位319得到数59，而 $\sqrt[3]{27} < \sqrt[3]{59} < \sqrt[3]{64}$ ，则 $3 < \sqrt[3]{59} < 4$ ，可得 $30 < \sqrt[3]{59319} < 40$ ，由此能确定59319的立方根的十位数是3，因此59319的立方根是39．

(1)、现在换一个数46656，按这种方法求立方根，请完成下列填空：

①它的立方根是位数；②它的立方根的个位数字是；

③46656的立方根是；

(2)、求195112的立方根．（过程可按题目中的步骤写）

查看试题解析