第五章《一次函数》提升卷—苏科版(2024)数学八(上)单元测
试卷更新日期:2025-10-12 类型:单元试卷
一、选择题:本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一个是正确的.每小题选对得3分,选错、不选或多选,均不得分.
-
1. 函数y=kx与y=﹣kx+k的大致图象是( )A、
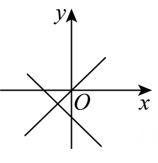 B、
B、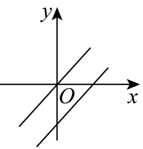 C、
C、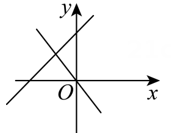 D、
D、 2. 对于一次函数 , 下列结论正确的是( )A、函数的图象不经过第四象限 B、函数的图象与轴的交点坐标是 C、函数的图象向下平移3个单位长度得的图象 D、若 , 两点在该函数图象上,且 , 则3. 已知直线y=x﹣2与y=mx﹣n相交于点M(3,b),则关于x , y的二元一次方程组的解为 ( )A、 B、 C、 D、4. 材料:甲开汽车,乙骑自行车从地沿一条笔直的公路匀速前往地,乙比甲先出发.设乙行驶的时间为 , 甲,乙两人之间的距离关于时间的函数图象如图所示.根据材料,获得正确的信息是( )
2. 对于一次函数 , 下列结论正确的是( )A、函数的图象不经过第四象限 B、函数的图象与轴的交点坐标是 C、函数的图象向下平移3个单位长度得的图象 D、若 , 两点在该函数图象上,且 , 则3. 已知直线y=x﹣2与y=mx﹣n相交于点M(3,b),则关于x , y的二元一次方程组的解为 ( )A、 B、 C、 D、4. 材料:甲开汽车,乙骑自行车从地沿一条笔直的公路匀速前往地,乙比甲先出发.设乙行驶的时间为 , 甲,乙两人之间的距离关于时间的函数图象如图所示.根据材料,获得正确的信息是( ) A、甲行驶的速度是 B、在甲出发后追上乙 C、 , 两地之间的距离为 D、甲比乙少行驶2小时5. 有一块长方形菜园 , 一边利用足够长的墙,另三边用长度为的篱笆围成,设长方形的长为 , 宽为 , 则下列函数图象能反映与关系的是
A、甲行驶的速度是 B、在甲出发后追上乙 C、 , 两地之间的距离为 D、甲比乙少行驶2小时5. 有一块长方形菜园 , 一边利用足够长的墙,另三边用长度为的篱笆围成,设长方形的长为 , 宽为 , 则下列函数图象能反映与关系的是 A、
A、 B、
B、 C、
C、 D、
D、 6. 如图①,在平面直角坐标系中,矩形 ABCD 在第一象限,且 BC∥x轴,直线y=2x+1沿x轴正方向平移,在平移过程中,直线被矩形 ABCD 截得的线段长为a,直线在x轴上平移的距离为b,a,b间的函数关系图象如图②所示,那么矩形ABCD 的面积为( ).
6. 如图①,在平面直角坐标系中,矩形 ABCD 在第一象限,且 BC∥x轴,直线y=2x+1沿x轴正方向平移,在平移过程中,直线被矩形 ABCD 截得的线段长为a,直线在x轴上平移的距离为b,a,b间的函数关系图象如图②所示,那么矩形ABCD 的面积为( ). A、 B、 C、8 D、107. 骑行山地自行车过程中,如果车座高度不合适,会使骑行者踩踏费力,甚至造成膝盖磨损。有一种雷蒙德测量方法:双腿站立,两脚(不穿鞋)间距15cm,测量禅部离地面的距离(单位:cm),得出的数据乘0.883就是相应的骑行时最合适的AC长度(由长度为48cm的立管AB和可调节的坐杆BC组成,如图所示)。设AC长度最合适时坐杆BC的长度为 , 则下列说法不正确的是( )
A、 B、 C、8 D、107. 骑行山地自行车过程中,如果车座高度不合适,会使骑行者踩踏费力,甚至造成膝盖磨损。有一种雷蒙德测量方法:双腿站立,两脚(不穿鞋)间距15cm,测量禅部离地面的距离(单位:cm),得出的数据乘0.883就是相应的骑行时最合适的AC长度(由长度为48cm的立管AB和可调节的坐杆BC组成,如图所示)。设AC长度最合适时坐杆BC的长度为 , 则下列说法不正确的是( ) A、若某人裆部离地面的距离为100cm,则他骑行最合适的
A、若某人裆部离地面的距离为100cm,则他骑行最合适的AC长是88.3cm
B、当x=100时,y=40.3 C、y与x的关系式为y=0.883x-48 D、若某人裆部离地面的距离为110cm,某山地车坐杆BC的最大调节长度为45cm,那么他适合骑该山地车8. “漏刻”是我国古代一种利用水流计时的工具(如图1),综合实践小组用甲、乙两个透明的竖直放置的容器和一根装有节流阀(控制水的流速)的软管,制作了类似“漏刻”的简易计时装置(如图2)。上午9:00,综合实践小组在甲容器里加满水,经过实验得到甲容器的水面高度h(cm)与流水时间t(min)的关系如图3所示,下列说法错误的是( ) A、甲容器的初始水面高度为30cm; B、14:00甲容器的水流光; C、甲容器的水面高度h与流水时间t的关系式为; D、11:00时甲容器的水面高度为12cm。
A、甲容器的初始水面高度为30cm; B、14:00甲容器的水流光; C、甲容器的水面高度h与流水时间t的关系式为; D、11:00时甲容器的水面高度为12cm。二、填空题:本大题共10小题,每小题3分,共30分.只要求填出最后结果.
-
9. 若y关于x的函数是一次函数,则m的值为 .10. 已知等腰三角形的周长为 , 设腰长为 , 底边为 , 试写出与的函数表达式 .11. 函数的自变量x的取值范围是 .12. 已知点 在一次函数 的图象上.当 时, ,则该函数图象不经过第象限。13. 已知一次函数(为常数,且),在的范围内,至少有一个的值使得 , 则的取值范围为 .14. 一个函数过点 , 且随增大而增大,请写出一个符合上述条件的函数表达式.15. 声音在空气中传播的速度(简称声速)是空气温度的一次函数,若当空气温度为时,声速为;当空气温度为时,声速为 , 则声速y与温度t的函数关系式为 .16. 如图,一次函数的图象与x轴交于点B,与正比例函数的图象交于点A,若点P是线段上的一个动点,则线段长的最小值为 .
 17. 在平面直角坐标系中,已知直线l:过点 , 且与坐标轴交于点 , 则当的面积为2,且直线与轴不平行时,直线的表达式为 .
17. 在平面直角坐标系中,已知直线l:过点 , 且与坐标轴交于点 , 则当的面积为2,且直线与轴不平行时,直线的表达式为 . 18. 如图1,11月10日晚,“深爱万物”—2023深圳人才嘉年华活动正式启动,千余架无人机在深圳人才公园上空上演“天空之舞”,为人才喝彩、向人才致敬.如图2的平面直角坐标系中,线段分别表示1号、2号无人机在队形变换中飞行高度 , 与飞行时间的函数关系,其中 , 线段与相交于点P , 轴于点B , 点A的横坐标为25.则在第秒时1号和2号无人机在同一高度.
18. 如图1,11月10日晚,“深爱万物”—2023深圳人才嘉年华活动正式启动,千余架无人机在深圳人才公园上空上演“天空之舞”,为人才喝彩、向人才致敬.如图2的平面直角坐标系中,线段分别表示1号、2号无人机在队形变换中飞行高度 , 与飞行时间的函数关系,其中 , 线段与相交于点P , 轴于点B , 点A的横坐标为25.则在第秒时1号和2号无人机在同一高度.
三、解答题:本大题10小题,共96分.
-
19. 设一次函数 , 为常数,的图象过 , 两点.(1)、求该函数表达式;(2)、若点在该函数图象上,求的值;(3)、设点在轴上,若 , 求点的坐标.20. 在平面直角坐标系中,给出如下新定义:对于任意一点P(x,y)和给定的正整数n,如果满足|x|+ny=n(y≥0),则把点P(x,y)称作“n-精致点”
 (1)、P(x,y)是“n-精致点”,当n=1,x=-时,y=.(2)、在第一象限内,当n=4时,
(1)、P(x,y)是“n-精致点”,当n=1,x=-时,y=.(2)、在第一象限内,当n=4时,①设“4-精致点”的横坐标为x,那么纵坐标可以用含x的代数式表示为 .
②如图直线1经过(5,0)和(0,-5)求出直线l所对应的函数表达式 , 并判断该直线在第一象限内是否存在“4-精致点”。如果有,请求出其“4-精致点的坐标,如果没有,请说明理由;
(3)、若直线y=2x+b上存在“4-精致点”请直接写出实数b的取值范围。21. 如图,一次函数的图象分别与x轴,y轴交于A、B两点,正比例函数的图象与交于点 . (1)、求m的值及的关系式;(2)、方程组的解为________;(3)、求的值.22. 如图,数学活动课上,为了测量学校旗杆的高度,小亮在地面平放一面镜子在镜子上做一个标记点C,小亮看着镜子来回移动,直至看到旗杆顶端点在镜子中的像与标记点C重合。经测量,小亮的眼睛离地面高度DE为1.6m,小亮与标记点C的距离CE为2m,标记点C与旗杆底部点B的距离BC为12m。
(1)、求m的值及的关系式;(2)、方程组的解为________;(3)、求的值.22. 如图,数学活动课上,为了测量学校旗杆的高度,小亮在地面平放一面镜子在镜子上做一个标记点C,小亮看着镜子来回移动,直至看到旗杆顶端点在镜子中的像与标记点C重合。经测量,小亮的眼睛离地面高度DE为1.6m,小亮与标记点C的距离CE为2m,标记点C与旗杆底部点B的距离BC为12m。 (1)、在图中建立适当的平面直角坐标系,并直接写出点C,D的坐标。(2)、在(1)的条件下,求直线AC的表达式及旗杆的高度。23. 工厂某车间需加工一批零件,甲组工人加工中因故障产检修机器一次,然后以原来的工作效率继续加工,由于时间紧任务重,乙组工人也加入共同加工零件。设甲组加工时间t(时),甲组加工买件的数量为y甲个。乙组加工数量为y乙个,其函数图象如图所示:
(1)、在图中建立适当的平面直角坐标系,并直接写出点C,D的坐标。(2)、在(1)的条件下,求直线AC的表达式及旗杆的高度。23. 工厂某车间需加工一批零件,甲组工人加工中因故障产检修机器一次,然后以原来的工作效率继续加工,由于时间紧任务重,乙组工人也加入共同加工零件。设甲组加工时间t(时),甲组加工买件的数量为y甲个。乙组加工数量为y乙个,其函数图象如图所示: (1)、求 乙与 之间的函数关系式,并写出 的取值范围;(2)、求 的值,并说明 的实际意义;(3)、甲组加工多长时间时,甲,乙两组加工夆件的总数为 480 个.24. 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发.设客车与甲地的距离为(千米),出租车与甲地的距离为(千米),两车行驶的时间为x(小时),、与x的函数关系图象如图所示:
(1)、求 乙与 之间的函数关系式,并写出 的取值范围;(2)、求 的值,并说明 的实际意义;(3)、甲组加工多长时间时,甲,乙两组加工夆件的总数为 480 个.24. 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发.设客车与甲地的距离为(千米),出租车与甲地的距离为(千米),两车行驶的时间为x(小时),、与x的函数关系图象如图所示: (1)、根据图象,直接写出、与x的函数表达式,并写出相应的自变量取值范围.(2)、运用(1)的结论,求当时两车之间的距离.(3)、若在出租车到达甲地之前,两车间的距离为S,求S与x的函数表达式.25. 已知一次函数 , 请回答下列问题:
(1)、根据图象,直接写出、与x的函数表达式,并写出相应的自变量取值范围.(2)、运用(1)的结论,求当时两车之间的距离.(3)、若在出租车到达甲地之前,两车间的距离为S,求S与x的函数表达式.25. 已知一次函数 , 请回答下列问题: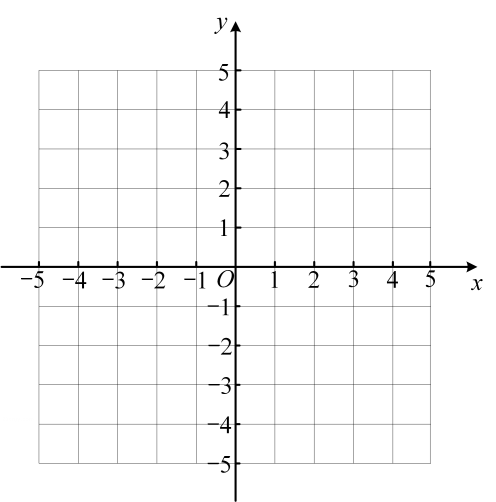 (1)、请用描点法画出它的图象:
(1)、请用描点法画出它的图象:解:列表:
x 0 m y 4 0 描点:以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点;
连线:把这两点连接起来,得到的图象;
表格中的值为 ;请在坐标系中画出的图象;
(2)、若一次函数的图象与一次函数图象关于轴对称,请画出一次函数的图象,并求出它的解析式;(3)、若平行于轴的直线分别交的图象,的图象于两点,已知的长为4,则点的横坐标是.26. 如图,将一块含角的直角三角板放置在直角坐标系中,其直角顶点O与原点重合,点A落在第一象限,点B的坐标为 , 与y轴交于点C. (1)、求点A的坐标.(2)、求的长.(3)、点P在x轴正半轴上,连结 . 当与的一个内角相等时,求所有满足条件的的长.27. 如图1,在同一平面直角坐标系中,直线:与直线:相交于点 , 与x轴交于点 , 直线与x轴交于点C.
(1)、求点A的坐标.(2)、求的长.(3)、点P在x轴正半轴上,连结 . 当与的一个内角相等时,求所有满足条件的的长.27. 如图1,在同一平面直角坐标系中,直线:与直线:相交于点 , 与x轴交于点 , 直线与x轴交于点C. (1)、填空: , , ;(2)、如图2,点D为线段上一动点,将沿直线翻折得到 , 线段交x轴于点F.
(1)、填空: , , ;(2)、如图2,点D为线段上一动点,将沿直线翻折得到 , 线段交x轴于点F.①求线段的长度;
②当点E落在y轴上时,求点E的坐标;
③若为直角三角形,请直接写出满足条件的点D的坐标.
28. 综合与实践生活中的数学:如何确定单肩包最佳背带长度
素材1
如图是一款单肩包,背带由双层部分、单层部分和调节扣构成.使用时可以通过调节扣加长或缩短单层部分的长度,使背带的总长度加长或缩短(总长度为单层部分与双层部分的长度和,其中调节扣的长度忽略不计).

素材2
对于该背包的背带长度进行测量,设双层的部分长度是 , 单层部分的长度是 , 得到如下数据:
双层部分长度
2
6
10
14
单层部分长度
116
108
100
92
70
素材3
单肩包的最佳背带总长度与身高比例为
素材4
小明爸爸准备购买此款背包.爸爸自然站立,将该背包的背带调节到最短提在手上,背带在背包的悬挂点离地面的高度为;已知爸爸的臂展和身高一样,且肩宽为 , 头顶到肩膀的垂直高度为总身高的 .
 (1)、【任务1】在平面直角坐标系中,以所测得数据中的为横坐标,以为纵坐标,描出所表示的点,并用光滑曲线连接,根据图象思考变量、是否满足一次函数关系.如果是,求出该函数的表达式,直接写出值并确定的取值范围.
(1)、【任务1】在平面直角坐标系中,以所测得数据中的为横坐标,以为纵坐标,描出所表示的点,并用光滑曲线连接,根据图象思考变量、是否满足一次函数关系.如果是,求出该函数的表达式,直接写出值并确定的取值范围. (2)、【任务2】设人身高为 , 当单肩包背带长度调整为最佳背带总长度时,求此时人身高与这款背包的背带双层部分的长度之间的函数表达式.(3)、当小明爸爸的单肩包背带长度调整为最佳背带总长度时.求此时双层部分的长度.
(2)、【任务2】设人身高为 , 当单肩包背带长度调整为最佳背带总长度时,求此时人身高与这款背包的背带双层部分的长度之间的函数表达式.(3)、当小明爸爸的单肩包背带长度调整为最佳背带总长度时.求此时双层部分的长度.