第四章《平面直角坐标系》提升卷—苏科版(2024)数学八(上)单元测
试卷更新日期:2025-10-12 类型:单元试卷
一、选择题:本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一个是正确的.每小题选对得3分,选错、不选或多选,均不得分.
-
1. 2024年10月30日,神舟19号在酒泉卫星发射中心成功发射。以下选项中,能够准确表示"酒泉卫星发射中心"地理位置的是( )A、北纬 , 东经 B、离北京市1500千米 C、在巴丹吉林沙漠深处 D、在中国甘肃2. 如图,在平面直角坐标系中,垂直轴,垂直轴,且 , , 则点的坐标为( )
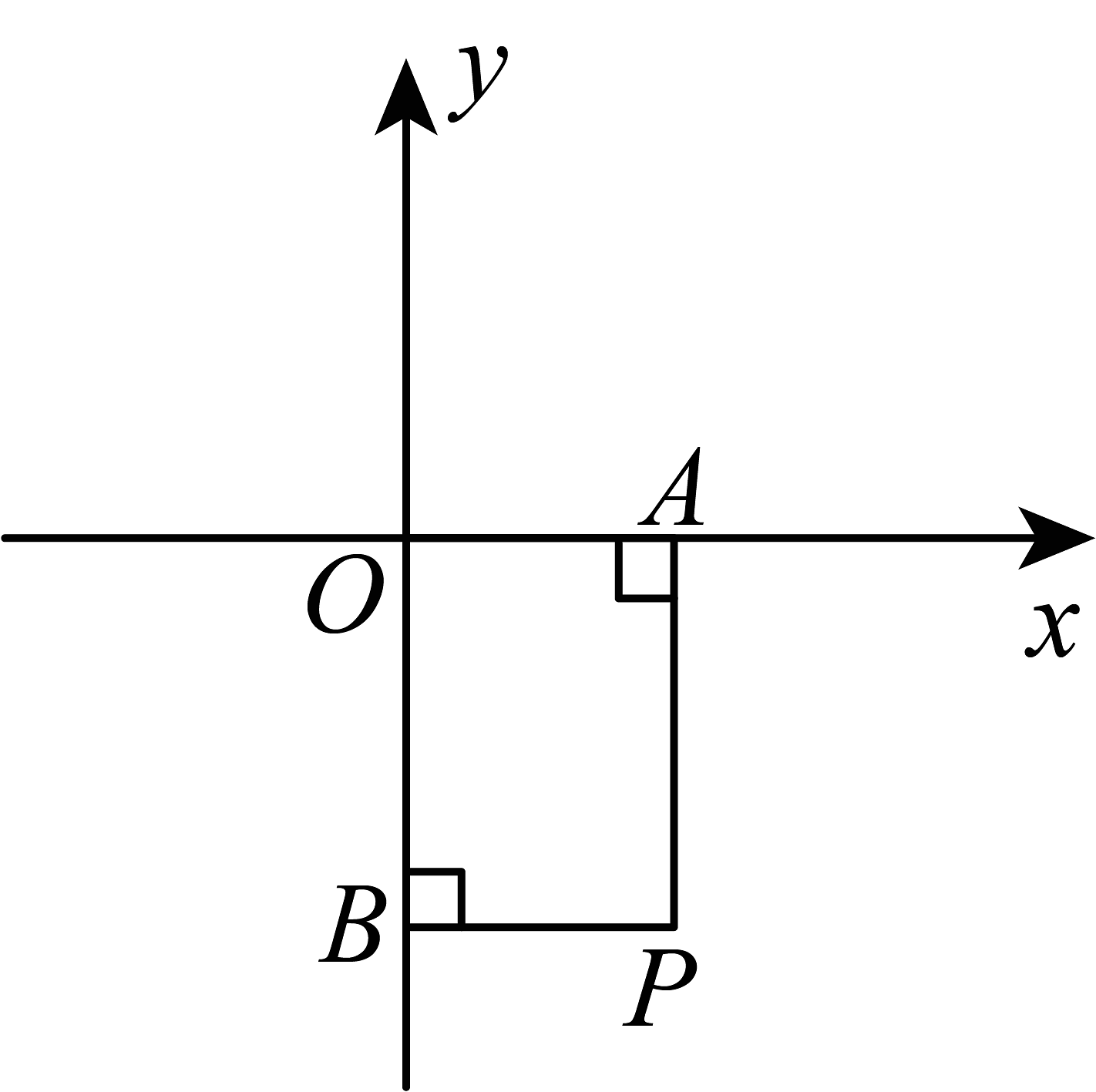 A、 B、 C、 D、3. 在平面直角坐标系中,点的坐标是 , 作点关于轴的对称点,得到点 , 再将点向下平移4个单位,得到点 , 则点的坐标是( )A、 B、 C、 D、4. 在平面直角坐标系中,已知点A(1,1),B(3,2),点C 在坐标轴上,若△ABC 是等腰三角形,则点C 的个数是( ).A、3 B、4 C、7 D、85. 如图,已知点 , A与关于y轴对称,连结 , 现将线段以点为中心顺时针旋转得 , 点 B的对应点的坐标为( )
A、 B、 C、 D、3. 在平面直角坐标系中,点的坐标是 , 作点关于轴的对称点,得到点 , 再将点向下平移4个单位,得到点 , 则点的坐标是( )A、 B、 C、 D、4. 在平面直角坐标系中,已知点A(1,1),B(3,2),点C 在坐标轴上,若△ABC 是等腰三角形,则点C 的个数是( ).A、3 B、4 C、7 D、85. 如图,已知点 , A与关于y轴对称,连结 , 现将线段以点为中心顺时针旋转得 , 点 B的对应点的坐标为( ) A、 B、 C、 D、6. 如图,在平面直角坐标系中,从点 , , 依此扩展下去,则的坐标为( )
A、 B、 C、 D、6. 如图,在平面直角坐标系中,从点 , , 依此扩展下去,则的坐标为( )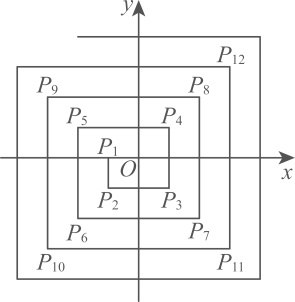 A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本大题共10小题,每小题3分,共30分.只要求填出最后结果.
-
7. 如图是嘉兴市部分景点位置示意图,若在正方形网格中建立适当的平面直角坐标系,使点A(烟雨楼)的坐标为 , 点B(子城)的坐标为 , 则点C(月河)的坐标为 .
 8. 在仪仗队列中,共有八列,每列8人,若战士甲站在第二列从前面数第3个,可以表示为 , 则战士乙站在第七列从前面数第2个,应表示为 .9. 在平面直角坐标系中,点A(3,a﹣b)与B(2a﹣b,﹣4)关于x轴对称,则= .10. 在直角坐标系中,点 , 点 , 的最小值为 , 最大值大于 , 则的取值范围 .11. 如图所示,点、分别是坐标轴上的点,且 , 轴,点在轴负半轴上, , 连接、相交于点 , 若四边形的面积为 , 长为1,则点的坐标为 .
8. 在仪仗队列中,共有八列,每列8人,若战士甲站在第二列从前面数第3个,可以表示为 , 则战士乙站在第七列从前面数第2个,应表示为 .9. 在平面直角坐标系中,点A(3,a﹣b)与B(2a﹣b,﹣4)关于x轴对称,则= .10. 在直角坐标系中,点 , 点 , 的最小值为 , 最大值大于 , 则的取值范围 .11. 如图所示,点、分别是坐标轴上的点,且 , 轴,点在轴负半轴上, , 连接、相交于点 , 若四边形的面积为 , 长为1,则点的坐标为 . 12. 如图,四盏灯笼的坐标分别是 , 要使四盏灯笼组成的图形关于轴对称,只需把灯笼向右平移个单位.
12. 如图,四盏灯笼的坐标分别是 , 要使四盏灯笼组成的图形关于轴对称,只需把灯笼向右平移个单位. 13. 如图,第一象限内有两点P(m-3,n),Q(m,n-2),将线段PQ平移使点P,Q分别落在两条坐标轴上,则点P平移后的对应点的坐标是.
13. 如图,第一象限内有两点P(m-3,n),Q(m,n-2),将线段PQ平移使点P,Q分别落在两条坐标轴上,则点P平移后的对应点的坐标是. 14. 如图,在平面直角坐标系中,点 , , 作 , 使与全等,则点C(不与点A重合)的坐标为 .
14. 如图,在平面直角坐标系中,点 , , 作 , 使与全等,则点C(不与点A重合)的坐标为 .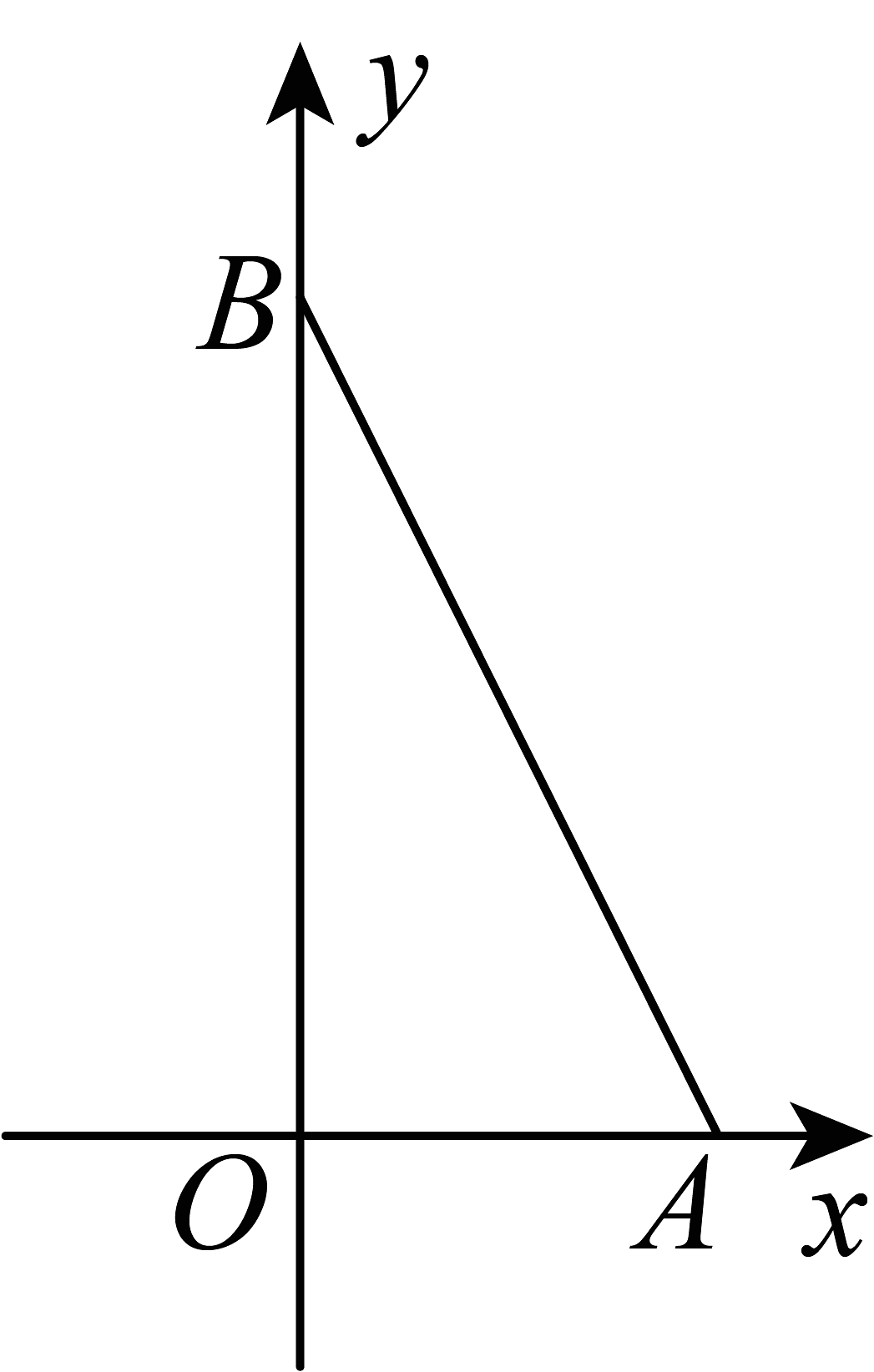 15. 如图,把平面内一条数轴x绕点O逆时针旋转角得到另一条数轴y , x轴和y轴构成一个平面斜坐标系.规定:已知点P是平面斜坐标系中任意一点,过点P作y轴的平行线交x轴于点A , 过点P作x轴的平行线交y轴于点B , 若点A在x轴上对应的实数为a , 点B在y轴上对应的实数为b , 则称有序实数对为点P的斜坐标.若点P的斜坐标为 , 点G的斜坐标为 , 连接 , 则线段的长度为 .
15. 如图,把平面内一条数轴x绕点O逆时针旋转角得到另一条数轴y , x轴和y轴构成一个平面斜坐标系.规定:已知点P是平面斜坐标系中任意一点,过点P作y轴的平行线交x轴于点A , 过点P作x轴的平行线交y轴于点B , 若点A在x轴上对应的实数为a , 点B在y轴上对应的实数为b , 则称有序实数对为点P的斜坐标.若点P的斜坐标为 , 点G的斜坐标为 , 连接 , 则线段的长度为 . 16. 如图六边形是正六边形,曲线…叫做正六边形的渐开线,满足 , , , …;点B、点A与点共线,点C、点B与点共线,点D、点C与点共线…,当点A坐标为 , 点B坐标为时,点的坐标是 .
16. 如图六边形是正六边形,曲线…叫做正六边形的渐开线,满足 , , , …;点B、点A与点共线,点C、点B与点共线,点D、点C与点共线…,当点A坐标为 , 点B坐标为时,点的坐标是 .
三、解答题:本大题10小题,共96分.
-
17. 如图,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3)将△ABC平移得到△A1B1C1 , 其中A的对应点是A1(2,1);
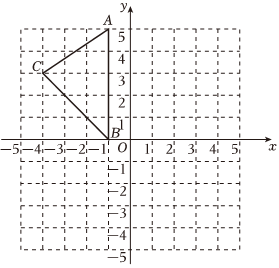 (1)、写出点B , C的对应点B1 , C1的坐标:B1 , C1;(2)、在图中画出△A1B1C1;(3)、设点P在x轴上,且△BCP的面积等于△ABC的面积,求出点P的坐标.18. 在平面直角坐标系中的位置如图所示.
(1)、写出点B , C的对应点B1 , C1的坐标:B1 , C1;(2)、在图中画出△A1B1C1;(3)、设点P在x轴上,且△BCP的面积等于△ABC的面积,求出点P的坐标.18. 在平面直角坐标系中的位置如图所示. (1)、请在图1中作关于x轴成轴对称的;(2)、在图2中将向右平移个单位,作出平移后的;则此三角形的面积为 ▲ .(3)、在轴上求作一点 , 使的值最小,点的坐标为 ▲ .19. 在一次“寻宝”游戏中,寻宝人已经找到了A(-2,3)和B(2,3)两个标志点,并且知道藏宝地点坐标为(-1,-1).请在下图中建立平面直角坐标系并确定宝藏的位置.
(1)、请在图1中作关于x轴成轴对称的;(2)、在图2中将向右平移个单位,作出平移后的;则此三角形的面积为 ▲ .(3)、在轴上求作一点 , 使的值最小,点的坐标为 ▲ .19. 在一次“寻宝”游戏中,寻宝人已经找到了A(-2,3)和B(2,3)两个标志点,并且知道藏宝地点坐标为(-1,-1).请在下图中建立平面直角坐标系并确定宝藏的位置. 20. 在直角坐标系中,有点A(3,0),B(0,4),若有一个直角三角形与Rt△ABO全等且它们只有一条公共直角边,请写出这些直角三角形各顶点的坐标(不要求写计算过程).(至少写出三个)
20. 在直角坐标系中,有点A(3,0),B(0,4),若有一个直角三角形与Rt△ABO全等且它们只有一条公共直角边,请写出这些直角三角形各顶点的坐标(不要求写计算过程).(至少写出三个) 21. 已知当m , n都是实数,且满足2m=8+n时,称p(m﹣1,)为“开心点”.例如点A(5,3)为“开心点”.
21. 已知当m , n都是实数,且满足2m=8+n时,称p(m﹣1,)为“开心点”.例如点A(5,3)为“开心点”.∵当A(5,3)时,m﹣1=5,=3,得m=6,n=4,∴2m=2×6=12,
8+n=8+4=12,∴2m=8+n . ∴A(5,3)是“开心点”.
(1)、判断点B(9,6)是否为“开心点”,并说明理由;(2)、若点M(a , 2a-3)是“开心点”,请判断点M在第几象限?并说明理由.22. 对于平面直角坐标系中的线段及点 , 给出如下定义:如果点满足 , 那么点就是线段的“关联点”.其中,当时,称为线段的“远关联点”;当时,称为线段的“近关联点”.
 (1)、如图1,当点坐标分别为和时,在 , , , 中,线段的“近关联点”有_______.(2)、如图2,点的坐标为 , 点在轴正半轴上, .
(1)、如图1,当点坐标分别为和时,在 , , , 中,线段的“近关联点”有_______.(2)、如图2,点的坐标为 , 点在轴正半轴上, .①如果点在轴上,且为线段的“关联点”,那么点的坐标为_______;
②如果点为线段的“远关联点”,那么点的纵坐标的取值范围是_______.
23. 在平面直角坐标系中,对于点P(x,y),我们把点叫作点P的前进点.已知点A1的前进点为A2 , 点A2的前进点为A3 , 点A3的前进点为A4……这样依次得到点A1 , A2 , A3 , A4 , …,Aₙ.(1)、若点A1的坐标为(3,1),写出点A2 , A3 , A4 , A5的坐标.(2)、从第(1)题的解答中,你发现了什么规律?按此规律,写出A2021的坐标.(3)、若点A1的坐标为(a,b),对于任意的正整数n,点A,均在x轴上方,则a,b应满足什么条件?24. 如图,在平面直角坐标系中,点O为坐标原点,的顶点 B在x轴的正半轴上,点A在y轴正半轴上,的面积为4,且 . (1)、求点 B 的坐标;(2)、过点A作的垂线,点C在直线的下方垂直y轴于点D,当时,求点C的坐标;(3)、在(2)条件下,连接 , 点E为中点,求长度.25. 综合与实践:(1)、问题背景:
(1)、求点 B 的坐标;(2)、过点A作的垂线,点C在直线的下方垂直y轴于点D,当时,求点C的坐标;(3)、在(2)条件下,连接 , 点E为中点,求长度.25. 综合与实践:(1)、问题背景:已知 , , , . 在平面直角坐标系中描出这几个点,并分别找到线段和中点、 , 然后写出它们的坐标,则 ▲ , ▲ .
 (2)、探究发现:
(2)、探究发现:结合上述计算结果,你能发现若线段的两个端点的坐标分别为 , , 则线段的中点坐标为 .
(3)、拓展应用:利用上述规律解决下列问题:已知三点 , , , 第四个点与点E、点F、点G中的一个点构成的线段的中点与另外两个端点构成的线段的中点重合,求点H的坐标.
26. “2024全球领导者大会”于10月在上海黄浦区举行.大会围绕能源与双碳、绿色金融、可持续发展、科技与公益等前沿议题,推动全球合作、发展与共赢.我们规定,在平面直角坐标系中,对于点作如下“可持续发展”变换:若 , 则作它关于x轴的对称点;若 , 则作它关于y轴的对称点.点作第一次“可持续发展”变换得到点 , 再将点作第二次“可持续发展”变换得到点 . 若与重合,我们称点为“可持续发展点”;若与不重合,我们称点为“合作共赢点”.(1)、将点作如上“可持续发展”变换,则点的坐标为_______,点的坐标为________,由此,点为“_______点”(填“可持续发展”或“合作共赢”);(2)、若点为第三象限中的一点,求证:必为“合作共赢点”,且;(3)、若点为第三象限中的一点,且 , , 若t为实数, , 当时,求出t的值和的坐标.