第三章《勾股定理》提升卷—苏科版(2024)数学八(上)单元测
试卷更新日期:2025-10-12 类型:单元试卷
一、选择题:本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一个是正确的.每小题选对得3分,选错、不选或多选,均不得分.
-
1. 如图,在中, , , 点A恰好落在数轴上表示的点上,以原点O为圆心,的长为半径画弧交数轴于点P,使点P落在点A的左侧,则点P所表示的数是( )
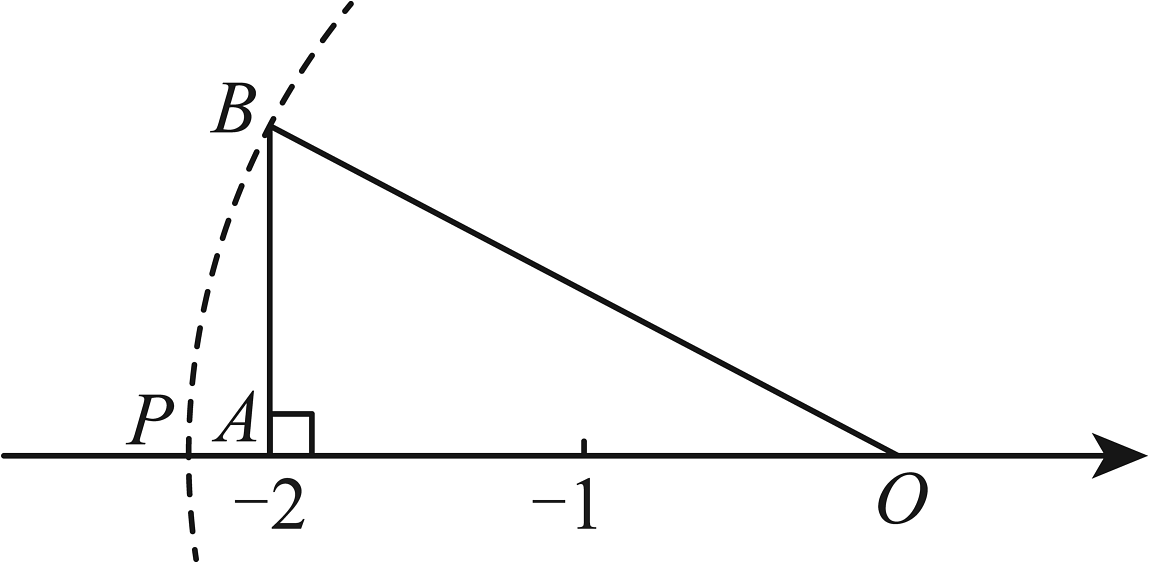 A、 B、 C、 D、2. 等腰三角形的周长为10cm,其中一边长为2cm,则该等腰三角形底边上的高为( )A、 B、 C、 D、 或3. “赵爽弦图”巧妙利用面积关系证明了勾股定理.如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼成的一个大正方形.设直角三角形的两条直角边长分别为m, . 若小正方形面积为5, , 则大正方形面积为( )
A、 B、 C、 D、2. 等腰三角形的周长为10cm,其中一边长为2cm,则该等腰三角形底边上的高为( )A、 B、 C、 D、 或3. “赵爽弦图”巧妙利用面积关系证明了勾股定理.如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼成的一个大正方形.设直角三角形的两条直角边长分别为m, . 若小正方形面积为5, , 则大正方形面积为( ) A、12 B、13 C、14 D、154. 如图,以的三边为直角边分别向外作等腰直角三角形.若 , 则图中阴影部分的面积为( )
A、12 B、13 C、14 D、154. 如图,以的三边为直角边分别向外作等腰直角三角形.若 , 则图中阴影部分的面积为( )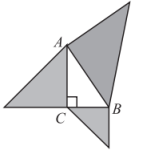 A、6 B、 C、 D、255. 下列各组中的三条线段,能构成直角三角形的是( )A、3,4,5 B、4,5,6 C、2, , 2 D、8,15,166. 已知△中,、、分别是、、的对边,下列条件中不能判断△是直角三角形的是( )A、 B、 C、 D、7. 九章算术中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?题意是:一根竹子原高1丈(1丈尺),中部有一处折断,竹稍触地面处离竹根4尺,试问折断处离地面多高?则折断处离地面的高度为( )
A、6 B、 C、 D、255. 下列各组中的三条线段,能构成直角三角形的是( )A、3,4,5 B、4,5,6 C、2, , 2 D、8,15,166. 已知△中,、、分别是、、的对边,下列条件中不能判断△是直角三角形的是( )A、 B、 C、 D、7. 九章算术中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?题意是:一根竹子原高1丈(1丈尺),中部有一处折断,竹稍触地面处离竹根4尺,试问折断处离地面多高?则折断处离地面的高度为( ) A、4.55尺 B、5.45尺 C、4.2尺 D、5.8尺8. 如图,有一只摆钟,摆锤看作一个点,当摆锤静止时,它离底座的垂直高度 , 当摆锤摆动到最高位置时,它离底座的垂直高度 , 此时摆锤与静止位置时的水平距离时,钟摆的长度是( )
A、4.55尺 B、5.45尺 C、4.2尺 D、5.8尺8. 如图,有一只摆钟,摆锤看作一个点,当摆锤静止时,它离底座的垂直高度 , 当摆锤摆动到最高位置时,它离底座的垂直高度 , 此时摆锤与静止位置时的水平距离时,钟摆的长度是( ) A、17 B、24 C、26 D、28
A、17 B、24 C、26 D、28二、填空题:本大题共10小题,每小题3分,共30分.只要求填出最后结果.
-
9. 已知中, , , , 且满足 . 则边上的高为 .10. 为了比较、 与 的大小,可以构造如图所示的图形进行推算,其中∠C=90°,BC=3,D 在BC 上且BD=AC=1,通过计算可得 (填“>”“<”或“=”).
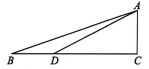 11. 如图,在Rt△ABC中,∠ABC=90°,AB=BC= , 将△ABC 绕点C 逆时针旋转60°,得到△MNC,连接 BM,则 BM 的长为.
11. 如图,在Rt△ABC中,∠ABC=90°,AB=BC= , 将△ABC 绕点C 逆时针旋转60°,得到△MNC,连接 BM,则 BM 的长为.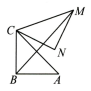 12. 如图,中, , , 则其内部五个小直角三角形的周长之和为 .
12. 如图,中, , , 则其内部五个小直角三角形的周长之和为 .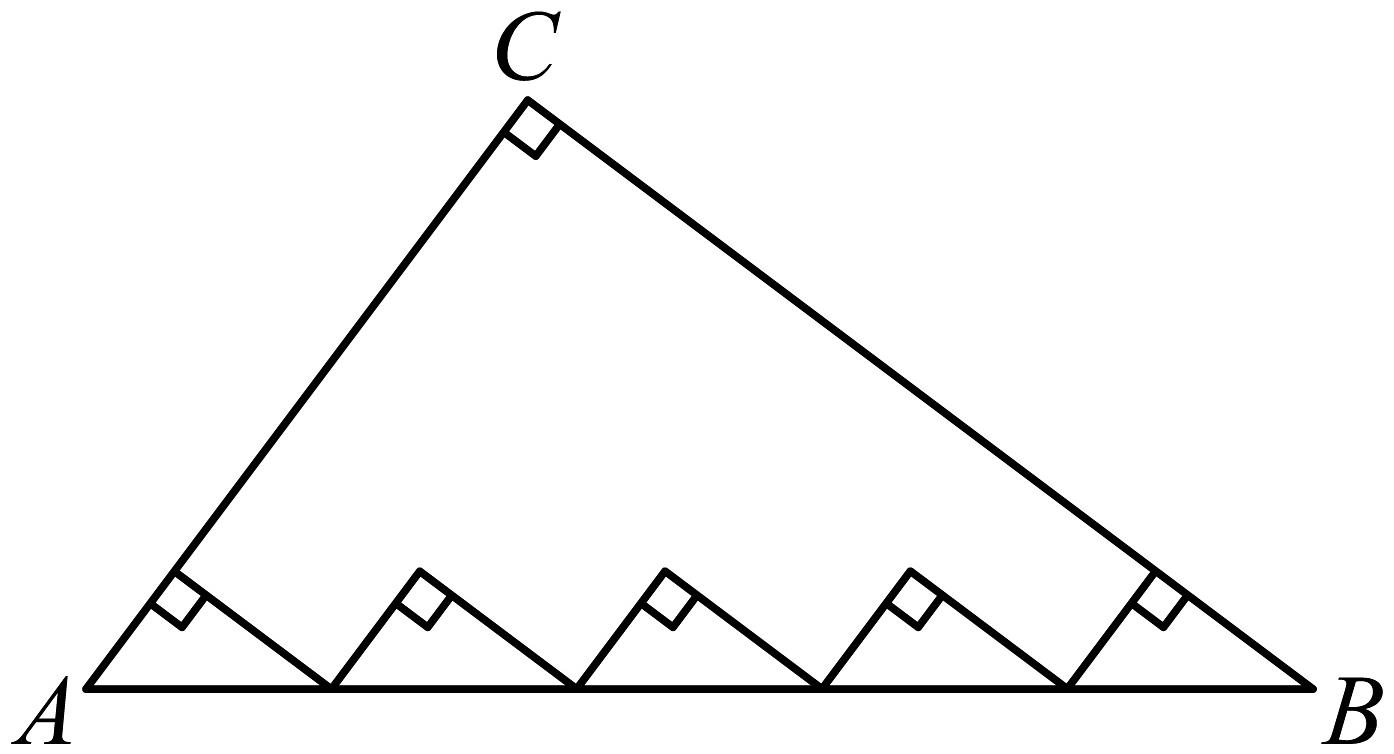 13. 如图是勾股树衍生图案,它由若干个正方形和直角三角形构成, , , , S4分别表示其对应正方形的面积,若已知上方左右两端的两个正方形的面积分别是64,9,则的值为
13. 如图是勾股树衍生图案,它由若干个正方形和直角三角形构成, , , , S4分别表示其对应正方形的面积,若已知上方左右两端的两个正方形的面积分别是64,9,则的值为 14. 临汾是帝尧之都,有着尧都之称.尧都华表柱身祥云腾龙,顶蹲冲天吼,底座浮雕长城和黄河壶口瀑布,是中华民族历史悠久、文化灿烂的标志.如图,在底面周长约为6米且带有层层回环不断的云朵石柱上,有一条雕龙从柱底沿立柱表面均匀地盘绕2圈到达柱顶正上方(从点A到点 , 为的中点),每根华表刻有雕龙的部分的柱身高约16米,则雕刻在石柱上的巨龙至少为 .
14. 临汾是帝尧之都,有着尧都之称.尧都华表柱身祥云腾龙,顶蹲冲天吼,底座浮雕长城和黄河壶口瀑布,是中华民族历史悠久、文化灿烂的标志.如图,在底面周长约为6米且带有层层回环不断的云朵石柱上,有一条雕龙从柱底沿立柱表面均匀地盘绕2圈到达柱顶正上方(从点A到点 , 为的中点),每根华表刻有雕龙的部分的柱身高约16米,则雕刻在石柱上的巨龙至少为 .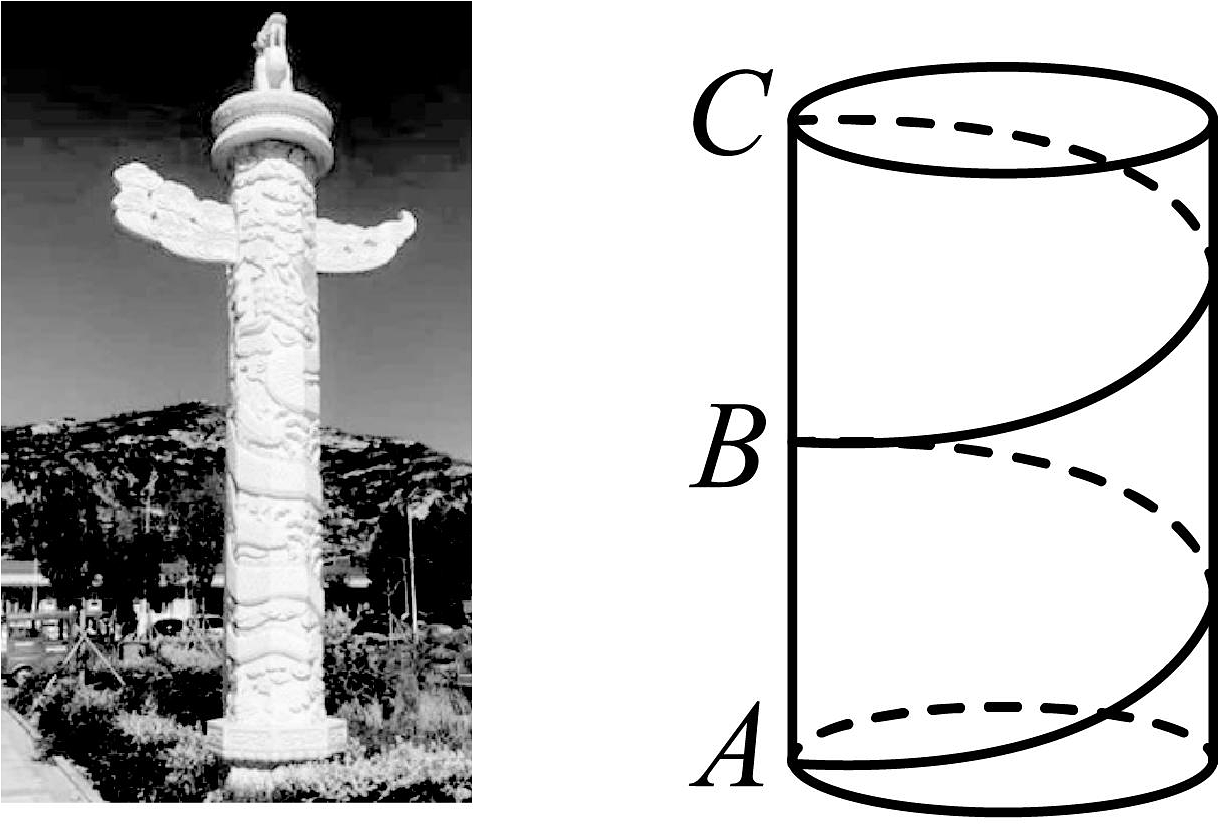 15. 等腰直角中, , 若点为边 , 上动点,且 , 则的最小值为 .
15. 等腰直角中, , 若点为边 , 上动点,且 , 则的最小值为 .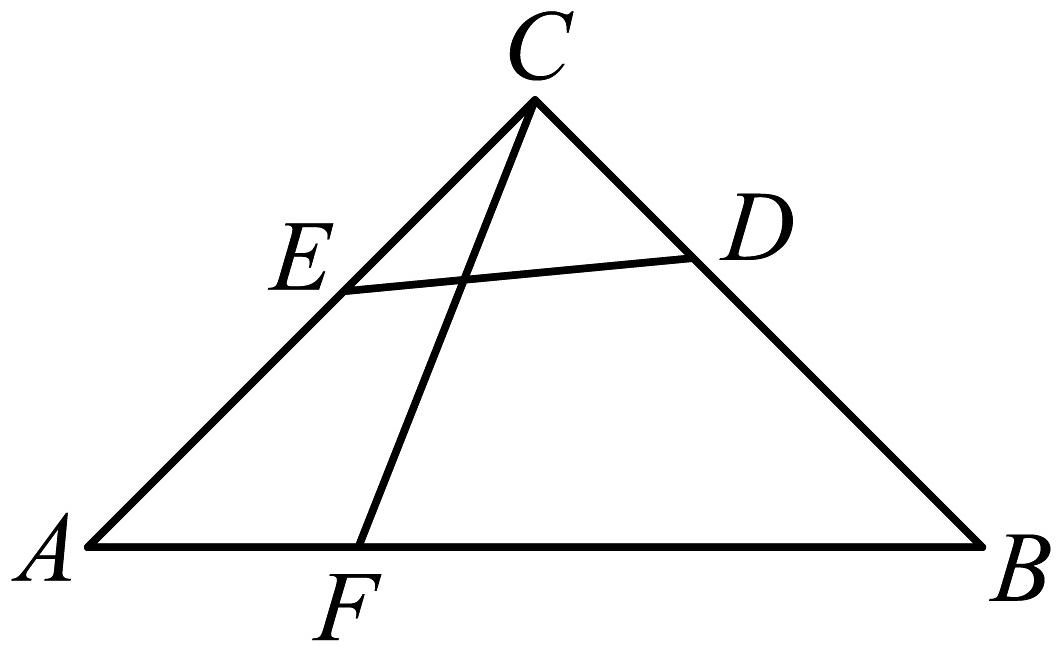 16. 如图,在中, , , , 点是内一点,则点到三个顶点的距离和的最小值是 .
16. 如图,在中, , , , 点是内一点,则点到三个顶点的距离和的最小值是 . 17. 如图,点P是在正内一点. , , , 将线段绕点A逆时针旋转得到线段 , 连接、 , 四边形的面积为 .
17. 如图,点P是在正内一点. , , , 将线段绕点A逆时针旋转得到线段 , 连接、 , 四边形的面积为 . 18. 科技改变生活,小莹计划购买一台圆形扫地机器人,有以下6种不同的尺寸可供选择,直径(单位:cm)分别是:34,34.5,37,39.5,40,42.如图是小莹家衣帽间的平面示意图,扫地机器人放置在该房间的角落(鞋柜、衣柜与地面均无缝隙),在没有障碍物阻挡的前提下,扫地机器人能从底座脱离后打扫全屋地面,小莹可选择的扫地机器人尺寸最多有种.
18. 科技改变生活,小莹计划购买一台圆形扫地机器人,有以下6种不同的尺寸可供选择,直径(单位:cm)分别是:34,34.5,37,39.5,40,42.如图是小莹家衣帽间的平面示意图,扫地机器人放置在该房间的角落(鞋柜、衣柜与地面均无缝隙),在没有障碍物阻挡的前提下,扫地机器人能从底座脱离后打扫全屋地面,小莹可选择的扫地机器人尺寸最多有种.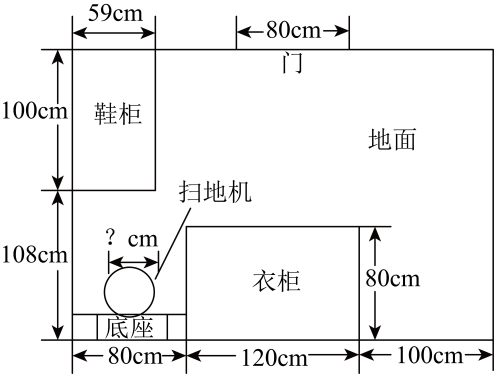
三、解答题:本大题10小题,共96分.
-
19. 图①、图②均是的正方形网格,每个小正方形的边长均为1,其顶点称为格点,的顶点均在格点上,只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.
 (1)、网格中的形状是______;(2)、在图①中确定一点 , 连接、 , 使与全等;(3)、在图②中的边上确定一点 , 连接 , 使与的面积比 .20. 阅读材料,解决问题:
(1)、网格中的形状是______;(2)、在图①中确定一点 , 连接、 , 使与全等;(3)、在图②中的边上确定一点 , 连接 , 使与的面积比 .20. 阅读材料,解决问题:我们可以在网格纸中通过构造三角形的方法来比较无理数的大小,例如在图1中,正方形网格纸中,每个小正方形的边长都是1,线段AB的长度为 , 线段BC的长度为 , 显然, .



 (1)、试比较与的大小,并说明理由;(2)、请在图2中尝试用构造图形的方法比较与的大小,在图3中尝试用构造图形的方法比较与的大小;(3)、请运用以上的构图思想,在图4中构图,并求出的最小值.21. 小明将要组织策划社区龙年春节联欢活动,活动需要准备一块会场背景板,形状如图所示.具体要求如下:在四边形中,连接 , , 米,米,米,米.
(1)、试比较与的大小,并说明理由;(2)、请在图2中尝试用构造图形的方法比较与的大小,在图3中尝试用构造图形的方法比较与的大小;(3)、请运用以上的构图思想,在图4中构图,并求出的最小值.21. 小明将要组织策划社区龙年春节联欢活动,活动需要准备一块会场背景板,形状如图所示.具体要求如下:在四边形中,连接 , , 米,米,米,米. (1)、求线段的长;(2)、若该背景板制作成本为10元/平方米,制作这样一块背景板需花费多少元?22. 探究:
(1)、求线段的长;(2)、若该背景板制作成本为10元/平方米,制作这样一块背景板需花费多少元?22. 探究: (1)、图(1)是由四个全等的直角三角形紧密拼接形成的飞镖状图形,若AB+AC=20,OC=5,求该飞镖状图形的面积.(2)、图(2)是由八个全等的直角三角形紧密拼接形成的大正方形ABCD,记图中正方形ABCD,正方形EFGH,正方形MNKT 的面积分别为 S1 , S2 , S3.若 求 的值.23. 数学兴趣小组利用所学数学知识来解决实际问题,实践报告如下:
(1)、图(1)是由四个全等的直角三角形紧密拼接形成的飞镖状图形,若AB+AC=20,OC=5,求该飞镖状图形的面积.(2)、图(2)是由八个全等的直角三角形紧密拼接形成的大正方形ABCD,记图中正方形ABCD,正方形EFGH,正方形MNKT 的面积分别为 S1 , S2 , S3.若 求 的值.23. 数学兴趣小组利用所学数学知识来解决实际问题,实践报告如下:活动课题 风筝离地面垂直高度探究
问题背景
风筝由我国古代劳动人民发明于东周春秋时期,距今已2000多年,相传墨翟以木头制成本鸟,研制三年而成,是人类最早的风筝起源.兴趣小组在放风筝时想测量风筝离地面的垂直高度.
测量数据抽象模型
小组成员测量了相关数据,并画出了如图所示的示意图,测得水平距离BC的长为15米,根据手中剩余线的长度计算出风筝线AB的长为17米,牵线放风筝的手到地面的距离为1.5米.
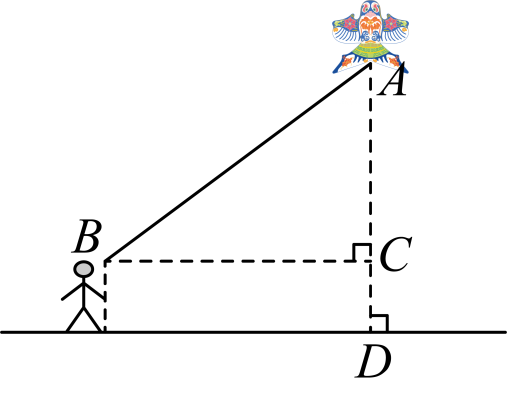
该报告还没有完成,请你帮助兴趣小组解决以下问题.
(1)、运用所学勾股定理相关知识,根据测量所得数据,计算出风筝离地面的垂直高度.(2)、如果想要风筝沿DA方向再上升12米,且BC长度不变,则应该再放出多少米线24. 数学家波利亚说过:“为了得到一个方程,我们必须把同一个量用两种不同的方法表示出来,即将一个量算两次,从而建立等量关系.”类似的,我们可以用两种不同的方法来表示同一个图形的面积,从而得到一个等式. (1)、如图 , 大正方形是由两个小正方形和两个形状大小完全相同的长方形拼成,请用两种不同的方法表示图中大正方形的面积.
(1)、如图 , 大正方形是由两个小正方形和两个形状大小完全相同的长方形拼成,请用两种不同的方法表示图中大正方形的面积.方法:;方法:;根据以上信息,可以得到的等式是;
(2)、如图 , 大正方形是由四个边长分别为的直角三角形(为斜边)和一个小正方形拼成,请用两种不同的方法分别表示小正方形的面积,并推导得到之间的数量关系;(3)、在()的条件下,若 , 求斜边的值.25. 某校八年级同学测量池塘两端A,B的距离,测量方案如下表:课题
测量池塘两端A,B的距离
测量工具
皮尺,标杆
测量方案示意图

测量步骤及数据
(1)利用标杆确定A,M,F在同一直线上,量得 , 然后找到了点N,且 , ;
(2)测得 , 再在的延长线方向确定点E,测得;
(3)在的延长线方向确定点D,使得;
(4)确定点C、点A和点E三点共线,测得;(5)测得 .
任务一
请你根据上述测量方案及数据,求出的长;
任务二
请你证明 .
26. 已知 , 点是平面内任意一点(不与点 , , 重合),若点与 , , 中的某两点的连线的夹角为直角,则称点为的一个“勾股点”.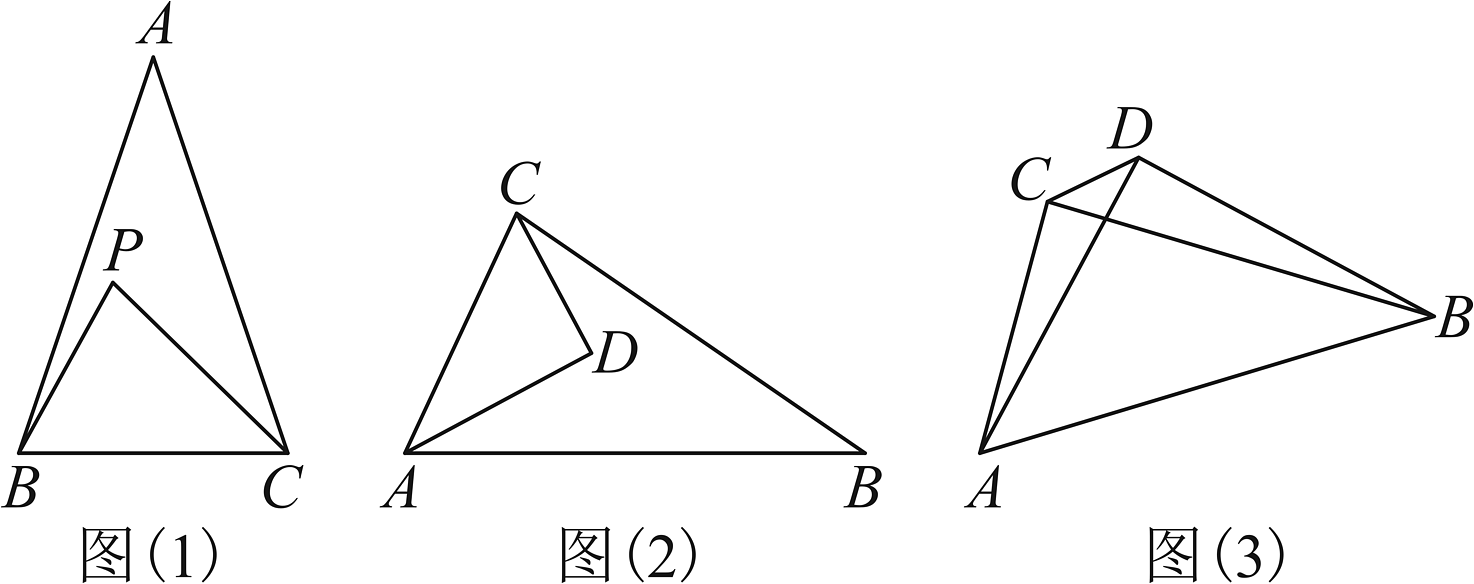 (1)、如图(1),若点是内一点, , , , 试说明点是的一个“勾股点”;(2)、如图(2),已知点是的一个“勾股点”, , 且 , 若 , , 求的长;(3)、如图(3),在中, , , 点为外一点, , , , 点能否是的“勾股点”,若能,求出的长;若不能,请说明理由.27. 勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.
(1)、如图(1),若点是内一点, , , , 试说明点是的一个“勾股点”;(2)、如图(2),已知点是的一个“勾股点”, , 且 , 若 , , 求的长;(3)、如图(3),在中, , , 点为外一点, , , , 点能否是的“勾股点”,若能,求出的长;若不能,请说明理由.27. 勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.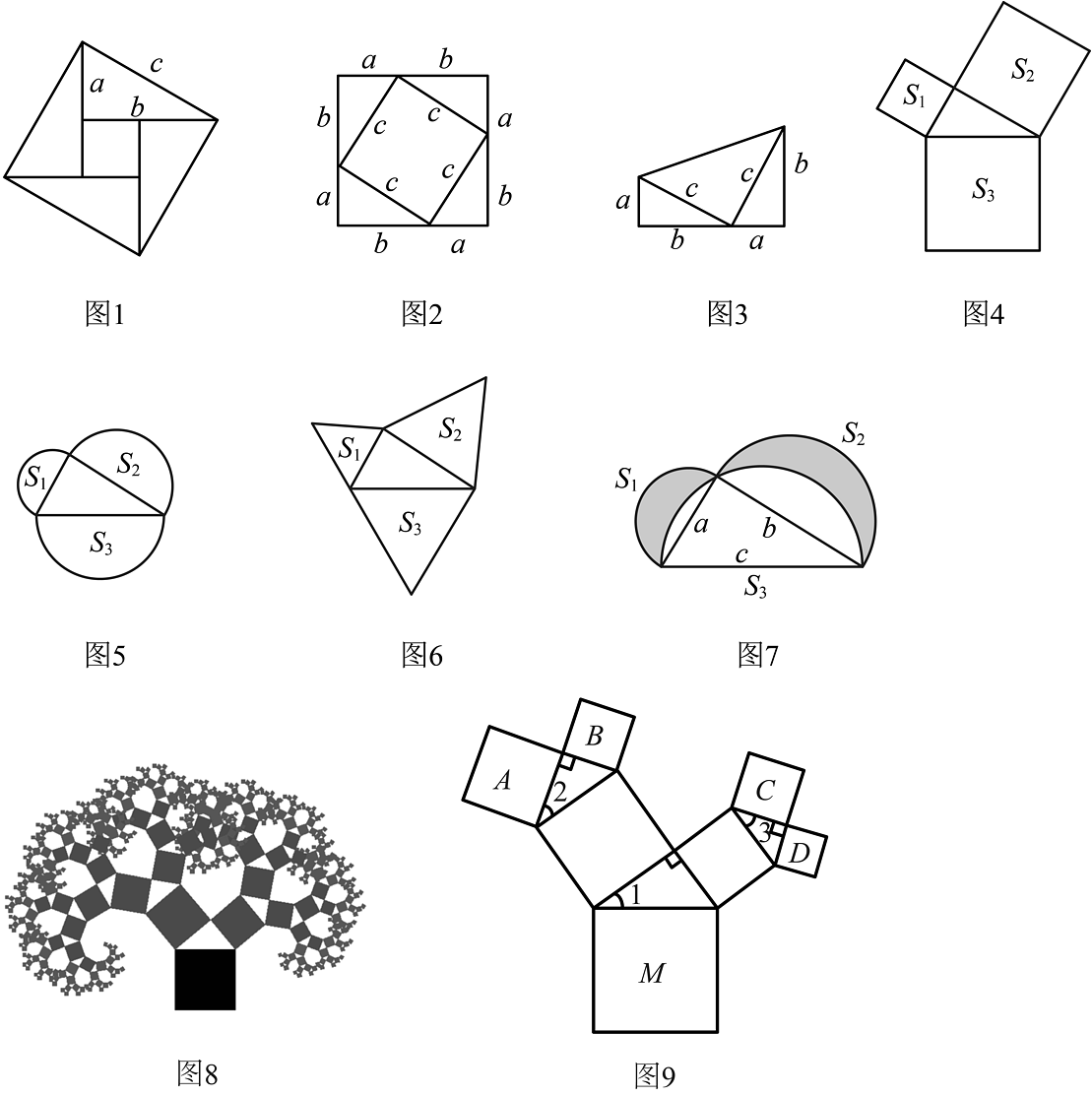 (1)、①如果用a,b和c分别表示直角三角形的两直角边和斜边,则______(用含有a,b和c的式子表示三者之间的等量关系);
(1)、①如果用a,b和c分别表示直角三角形的两直角边和斜边,则______(用含有a,b和c的式子表示三者之间的等量关系);②勾股定理的证明,人们已经找到了400多种方法,请从下列几种常见的证明方法中任选一种来证明该定理;(以下图形均满足证明勾股定理所需的条件)
(2)、①如图4、5、6,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足的有______个;②如图7所示,分别以直角三角形两直角边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为 , , 直角三角形面积为 , 请判断 , , 的关系并证明;
(3)、如果以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到如图8所示的“勾股树”.在如图9所示的“勾股树”的某部分图形中,设大正方形M的边长为定值m,四个小正方形A,B,C,D的边长分别为a,b,c,d,已知 , 则当变化时,回答下列问题:(结果可用含m的式子表示)则:①______.
②b与c的关系为______,a与d的关系为______.