人教版七（上）数学第五单元质量检测培优卷

试卷更新日期：2025-10-10 类型：单元试卷

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的。

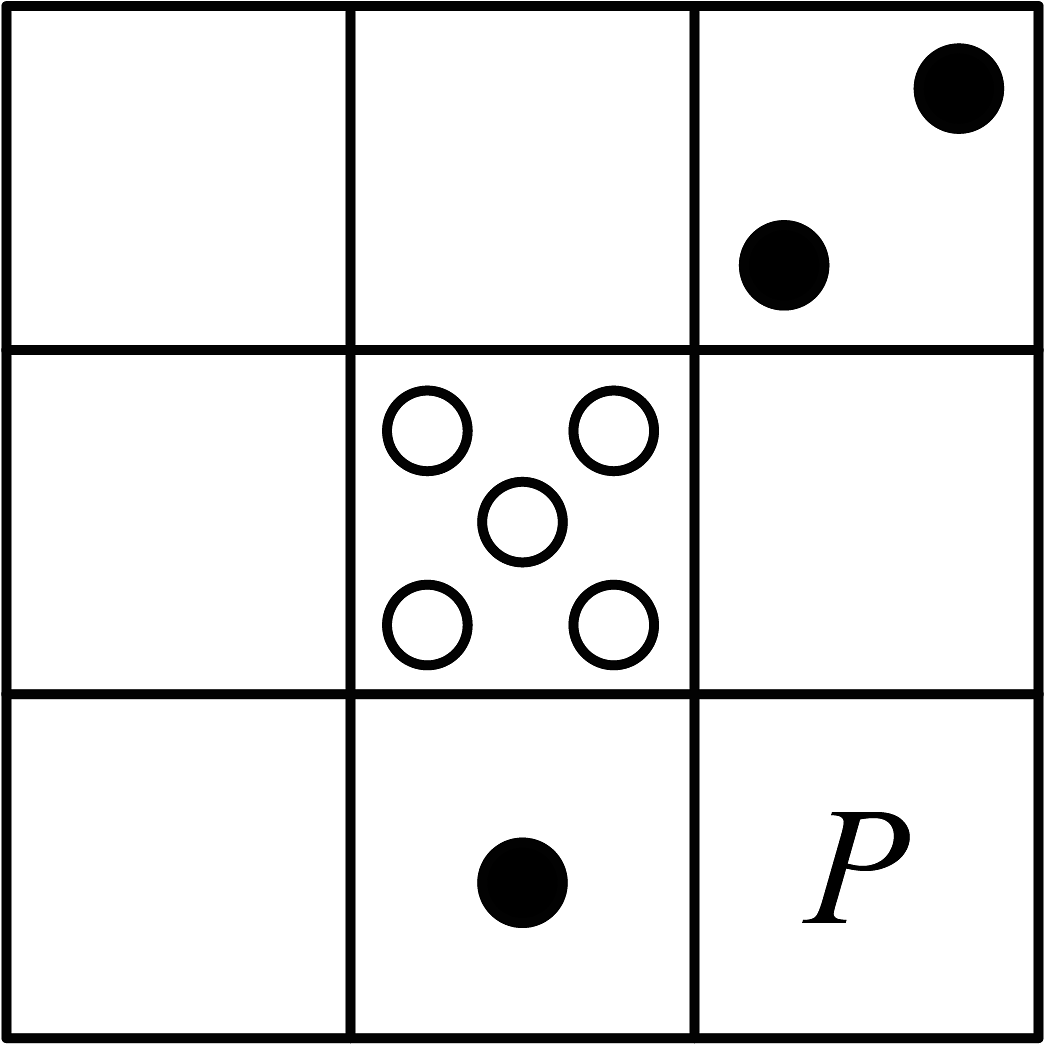
1. 我国古代的“河图”是由 $3 \times 3$ 的方格构成的，每个方格内均有．数目（个数为1～9）不同的点图，用实心点“●”表示正数，空心点“○”表示负数．每一行、每一列以及每一条对角线上的三个点图的点数之和均相等．如图，给出了“河图”的部分点图，请你推算出P处所对应的点图是（）

A、 B、 C、 D、

查看试题解析
2. 《周髀算经》是我国现存最早的数理天文著作.书中记载这样一道题：“今有女子不善织，日减功迟.初日织五尺，末日织一尺，今三十日织讫.问织几何?”其大意是现有一个不擅长织布的女子，织布的速度越来越慢，并且每天减少的数量相同，第一天织了五尺布，最后一天仅织了一尺布，30天完工.问：一共织了多少布?由题意，得该女子一共织布( )

A、45尺 B、88尺 C、90尺 D、98尺

查看试题解析
3. 长方形 $R_{1}, R_{2}$ 和正方形 $S_{1}, S_{2}, S_{3}$ 3按如图方式摆放成一个长为3322、宽为2020的长方形，则 S₂的边长为( ).

A、651 B、655 C、656 D、662 E、666

查看试题解析
4. 现有m辆客车、n个人．若每辆客车乘40人，则还有10人不能上车：若每辆客车乘43人，则只有1人不能上车据此列出下列四个等式：① $40 m + 10 = 43 m - 1$ ；② $\frac{n + 10}{40} = \frac{n + 1}{43}$ ；③ $\frac{n - 10}{40} = \frac{n - 1}{43}$ ；④ $40 m + 10 = 43 m + 1$ ．其中正确的是( )

A、①② B、②④ C、②③ D、③④

查看试题解析
5. 已知关于x的方程 $x - \frac{4 - a x}{6} = \frac{x + 4}{3} - 1$ 的解是正整数，则符合条件的所有整数a的积为( )

A、-12 B、-4 C、12 D、36

查看试题解析
6. 我国古代数学名著《算法统宗》中，有一道“群羊逐草”的问题，大意是：牧童甲在草原上放羊，乙牵着一只羊来，并问甲：“你的羊群有100只吗？”甲答：“如果在这群羊里加上同样的一群，再加上半群，四分之一群，再加上你的一只，就是100只。”问牧童甲赶着多少只羊？若设牧童甲赶着x只羊，则下列方程中，正确的是（）

A、 $x + \frac{1}{2} x + \frac{1}{4} x = 100 + 1$ B、 $x + \frac{1}{2} x + \frac{1}{4} x = 100 - 1$ C、 $x + x + \frac{1}{2} x + \frac{1}{4} x = 100 + 1$ D、 $x + x + \frac{1}{2} x + \frac{1}{4} x = 100 - 1$

查看试题解析
7. “幻方”最早源于我国，古人称之为纵横图．在图中，各行、各列及各条对角线上的三个数字之和均相等，对于下列两个结论的判断正确的是（）
结论Ⅰ：a的值为 $- 5$ ；结论Ⅱ： $a > b$

A、Ⅰ和Ⅱ都对 B、Ⅰ和Ⅱ都不对 C、Ⅰ不对Ⅱ对 D、Ⅰ对Ⅱ不对

查看试题解析
8. 阅读：关于x方程ax=b在不同的条件下解的情况如下：（1）当a≠0时，有唯一解x= $\frac{b}{a}$ ；（2）当a=0，b=0时有无数解；（3）当a=0，b≠0时无解．请你根据以上知识作答：已知关于x的方程 $\frac{x}{3}$ a= $\frac{x}{2}$ ﹣ $\frac{1}{6}$ （x﹣6）无解，则a的值是（）

A、1 B、﹣1 C、±1 D、a≠1

查看试题解析
9. “幻方”最早记载于春秋时期的《大戴礼记》中，如图1所示，每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等，现-1，2，-2，-4，5，-5，6，8 填入如图2所示的 “幻方” 中，部分数据已填入，则图中 $a + b + c - d$ 的值为（　　）

A、4 B、5 C、6 D、7

查看试题解析

10. 参加医疗保险，住院治疗的病人享受分段报销，保险公司制定的报销细则如下表．某人住院治疗后得到保险公司报销金额是1100元，那么此人住院的医疗费是（）

住院医疗费（元）	报销率（％）
不超过500元的部分	0
超过500 $\sim$ 1000元的部分	60
超过1000 $\sim$ 3000元的部分	80
……

A、1000元 B、1250元 C、1500元 D、2000元

查看试题解析

二、填空题：本大题共5小题，每小题3分，共15分.

11. 若关于x的一元一次方程 $\frac{1}{2018}$ x+2018＝2x+m的解为x＝2018，则关于y的一元一次方程 $\frac{1}{2018}$ y+2018+ $\frac{1}{2018}$ ＝2y+m+2的解为．

查看试题解析
12. 方程 $\frac{1}{9} {\frac{1}{7} [\frac{1}{5} (\frac{x + 2}{3} + 4) + 6\} = 1$ 的解是.

查看试题解析
13. 关于x的一元一次方程 $\frac{2021 - x}{2020} + \frac{2022 - x}{2021} = \frac{2023 - x}{2022} + \frac{2024 - x}{2023}$ 的解是。

查看试题解析
14. 按下面的程序计算：

如果输入 $x$ 的值是正整数，输出结果是 $214$ ，那么满足条件的 $x$ 的值可以是．

查看试题解析
15. 规定：对于确定位置的三个数a，b，c，计算 $a - b ， \frac{a - c}{2} ， \frac{b - c}{3}$ ，将这三个数的最小值称为a，b，c的“白马数”．例如，对于1，-2，3 ，因为 $1 - (- 2) = 3 ， \frac{1 - 3}{2} = - 1 ， \frac{- 2 - 3}{3} = - \frac{5}{3}$ ．所以1，-2 ，3的“白马数”为 $- \frac{5}{3}$ ．调整-1，6，x这三个数的位置，得到不同的“白马数”，若其中的一个“白马数”为2，则x＝．

查看试题解析

三、解答题：本大题共8小题，共75分.

16. 解下列方程：

(1)、 $\frac{x - 1}{3} - \frac{x + 2}{6} = \frac{4 - x}{2}$

(2)、 $\frac{0.4 + 0.9}{0.5} \frac{0.03 + 0.02 x}{0.03} = \frac{x - 5}{2}$

(3)、278（x﹣3）﹣463（6﹣2x）﹣888（7﹣21x）＝0

(4)、 $\frac{1}{2} {\frac{1}{2} [\frac{1}{2} (\frac{1}{2} x - 3) - 3] - 3} - 3 = 0$

查看试题解析
17. 观察下面有规律排列的三行数：

(1)、第一行数中，第7个数是______，第8个数是______

(2)、观察第二行、第三行数与第一行数的关系，解决下列问题：
①第二行数中，第7个数是______，第三行数中，第7个数是______；
②取每行数的第2022个数，计算这三个数的和是______；
③如图，在第二行、第三行数中，用两个长方形组成“阶梯形”方框，框住4个数，左右移动“阶梯形”方框，是否存在框住的4个数的和为 $- 5118$ ，若存在，求这四个数中最左边的数，若不存在，请说明理由．

查看试题解析
18. 元旦期间，七(1)班的小明、丽丽等同学随家长一同到某公园游玩.票价说明及小明与他爸爸的对话如图所示，试根据图中的信息解答下列问题：

(1)、他们一共去了几个成人，几个学生?

(2)、请你帮助小明算一算，用哪种方式购票更省钱?并说明理由.

(3)、买完票后，小明发现七(2)班的张小涛等8名同学和他们的12名家长也来买票，请你为他们设计出最省钱的购票方案，并求出此时的购票费用.

查看试题解析
19. 如图，在数轴上，点 $A$ 表示 $- 10$ ，点 $B$ 表示11，点 $C$ 表示18．动点 $P$ 从点 $A$ 出发，沿数轴正方向以每秒4个单位的速度匀速运动；同时，动点 $Q$ 从点 $C$ 出发沿数轴负方向以每秒2个单位的速度匀速运动．设运动时间为 $t$ 秒．

(1)、当 $t$ 为何值时， $P$ 、 $Q$ 两点相遇？相遇点 $M$ 所对应的数是多少？

(2)、在点 $Q$ 出发后到达点 $B$ 之前，求 $t$ 为何值时，点 $P$ 到点 $O$ 的距离与点 $Q$ 到点 $B$ 的距离相等；

(3)、在点 $P$ 向右运动的过程中， $N$ 是 $A P$ 的中点，在点 $P$ 到达点 $C$ 之前，求 $2 C N - P C$ 的值．

查看试题解析

20. 平价商场经销的甲、乙两种商品，甲种商品每件售价

90

元，利润率为

50 %

；乙种商品每件进价

50

元，售价

80

元：

(1)、甲种商品每件进价为元，每件乙种商品利润率为；

(2)、若该商场同时购进甲、乙两种商品共

50

件，恰好总进价为

2800

元，求购进乙种商品多少件？

(3)、在“元旦”期间，该商场只对甲乙两种商品进行如下的优惠促销活动：

打折前一次性购物总金额	优惠措施
少于等于 $400$ 元	不优惠
超过 $400$ 元，但不超过 $600$ 元	按售价打九折
超过 $600$ 元	其中 $600$ 元部分八折优惠，超过 $600$ 元的部分打六折优惠

按上述优惠条件，若小华一次性购买乙种商品实际付款 $504$ 元，求小华在该商场购买乙种商品多少件？

查看试题解析

21. 某加工厂利用图1所示的长方形和正方形铁片(长方形的宽与正方形的边长相等)，焊接成如图2所示的A型铁盒与B型铁盒，两种铁盒均无盖。

(1)、现在要做a个A型铁盒和b个B型铁盒，共需要张长方形铁片，张正方形铁片。

(2)、现有m张正方形铁片，n张长方形铁片，若这些铁片全部用完时，所制作的A，B型两种铁盒的数量恰好相等，m，n应满足怎样的数量关系?

(3)、现有正方形铁片50张，长方形铁片100张，若这些铁片恰好用完，则可制作A，B型两种铁盒各多少个?

查看试题解析

22.

活动目标：计算水费与用水量
素材1	为增强公民节水意识，合理利用水资源，采用“阶梯计价”.
素材2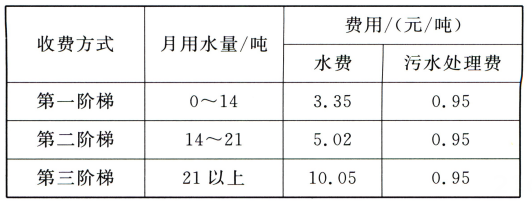
素材3	某用户 2023年2月份用水15 吨，则各种费用如下：
问题解决
⑴任务1	确定污水处理费	已知某用户2023年12月份所缴水费中，自来水费为66.98元，求该用户12月份需缴污水处理费多少元?
⑵任务2	确定水费	某用户 2023年11月用水a 吨，则应缴水费多少元?
⑶任务3	确定用水量	如果该用户2023年5，6月份共用水42吨(6月份用水量超过5月份用水量)，共缴水费209.01元，则该用户5，6月份各用水多少吨?

查看试题解析

23. 阅读下面一段文字．
【问题】我们知道整数和分数统称为有理数，那么无限循环小数 $0 . \dot{3}$ 是有理数吗？
【探求】步骤①：设 $x = 0 . \dot{3}$ ，
步骤②： $10 x = 10 \times 0 . \dot{3}$ ，
步骤③： $10 x = 3 . \dot{3}$ ，
步骤④：10x＝3＋x ，解得 $x = \frac{3}{9}$ ，即 $0 . \dot{3} = \frac{3}{9}$ ，从而可知 $0 . \dot{3}$ 是有理数．
根据对这段文字的理解，请你回答下列问题：

(1)、步骤①到步骤②的依据是；

(2)、依照上述探求过程，请尝试把 $0 . \dot{3} \dot{7}$ 化为分数形式．
步骤①：设 $y = 0 . \dot{3} \dot{7}$ ，
步骤②： $100 y = 100 \times 0 . \dot{3} \dot{7}$ ，
步骤③：；
步骤④：解得y＝；

(3)、请你将 $0 . \dot{4} \dot{5}$ 化为分数形式．

(4)、思考 $0 . \dot{9} 5 \dot{9}$ 可以化为分数形式吗？若能，请直接写出答案，不能，则说明理由．

查看试题解析