人教版七（上）数学第五单元质量检测提升卷

试卷更新日期：2025-10-10 类型：单元试卷

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 下列式子中，方程的个数是（）
$① 3 \times 3 + 1 = 5 \times 2$ ； $② {(y - 2)}^{2} \geq 0$ ； $③ 3 x + 1 = 5 y$ ； $④ 7 x - 1 = \frac{1}{2} x + 4$ ； $⑤ x + y + z$ ；

A、2 B、3 C、4 D、5

查看试题解析
2. 以下等式变形：①若 $\frac{x}{y} = 1 ，$ 则 $\frac{y}{x} = 1 ；$ ②若 ax+b= ay+b，则x=y；③若 $\frac{x}{a} + 1 = \frac{y}{a} + 1 ，$ 则x=y；④若x=y，则 $\frac{x}{a^{2} + 1} = \frac{y}{a^{2} + 1} .$ 其中正确的有( )

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 若方程 $5 x - 6 = - 3 x + 10$ 和 $3 x - 2 m = 10$ 的解相同，则 $m$ 的值为（）

A、 $- 2$ B、2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
4. 使得关于x 的方程 $x - \frac{4 - a x}{6} = \frac{x + 4}{3} - 1$ 的解是正整数的所有整数a的积为( )

A、12 B、-12 C、6 D、-6

查看试题解析
5. 某同学在解关于x的方程5a-x=13时，误将-x看成了+x，得到方程的解为x=-2，则a的值为( )

A、3 B、 $\frac{11}{5}$ C、4 D、1

查看试题解析
6. 新定义：a⊕b=3a-b。若x⊕(2⊕3)=1，则x等于 ( )

A、3 B、8 C、 $\frac{4}{3}$ D、 $\frac{1}{6}$

查看试题解析
7. 下列解一元一次方程的过程中，正确的是( )

A、方程x-2(3-x)=1去括号，得x-6+2x=1 B、方程3x+2=2x-2移项，得3x-2x=-2+2 C、方程 $\frac{2 x + 1}{3} - 1 = x$ 去分母，得2x+1-1=3x D、方程 $\frac{0.1 x - 2}{0.2} - \frac{0.2 x + 0.1}{0.5} = 1$ 分母化为整数，得 $\frac{x - 2}{2} - \frac{2 x + 1}{5} = 1$

查看试题解析
8. 在《算法统宗》中有这样一个问题：牧童分杏各争竟，不知人数不知杏。三人五个多十枚，四人八枚两个剩。问：有几个牧童?题目大意：牧童们要分一堆杏，不知道人数也不知道有多少个杏。若3人一组，每组5个杏，则多10个杏；若4人一组，每组8个，则多2个杏。有多少个牧童?设有x个牧童，则可列方程为（）

A、 $\frac{5 x - 10}{3} = \frac{8 x - 2}{4}$ B、15x+10=32x+2 C、 $\frac{x}{5} \times 3 - 10 = \frac{x}{8} \times 4 - 2$ D、 $\frac{x}{3} \times 5 + 10 = \frac{x}{4} \times 8 + 2$

查看试题解析
9. 如果 $a 、 b$ 是定值，且关于x的方程 $\frac{2 k x + a}{3} = 2 + \frac{x + b k}{6}$ ，无论k为何值时，它的解总是 $x = 1$ 那么 $2 a + b$ 的值是（）

A、15 B、16 C、17 D、18

查看试题解析
10. 若关于x的一元一次方程 $\frac{1}{2024} x + 3 = 2 x + b$ 的解为x=-3，则关于y的一元一次方程 $\frac{1}{2024} \cdot$ $(y + 1) + 3 = 2 (y + 1) + b$ 的解为( )

A、y=1 B、y=-2 C、y=-3 D、y=-4

查看试题解析

二、填空题：本大题共5小题，每小题3分，共15分.

11. 已知关于x的方程9x-3=kx+14有整数解，那么满足条件的所有整数k=.

查看试题解析
12. 将等式5(x+1)=3(x+1)的两边同时除以(x+1)，得到一个错误的结论5=3，错误的原因是.

查看试题解析
13. 某商店一款无线耳机按进价提高30%后标价，再优惠15 元销售，能获毛利润 75 元，则销售这款耳机的毛利率是.（毛利率= $\frac{售价 - 进价}{售价}$ ）

查看试题解析
14. 对于两个不相等的有理数a，b，我们规定符号 min{a，b}表示a，b两数中较小的数，例如min{2，-3}=-3。按照这个规定，方程min{x，-x}=-3x-12的解为。

查看试题解析
15. 由于换季，商场准备对某商品打折出售，如果按原售价的七折出售，将亏损40元，而按原售价的八五折出售，将盈利20元，则该商品的进货价为元．

查看试题解析

三、解答题：本大题共8小题，共75分.

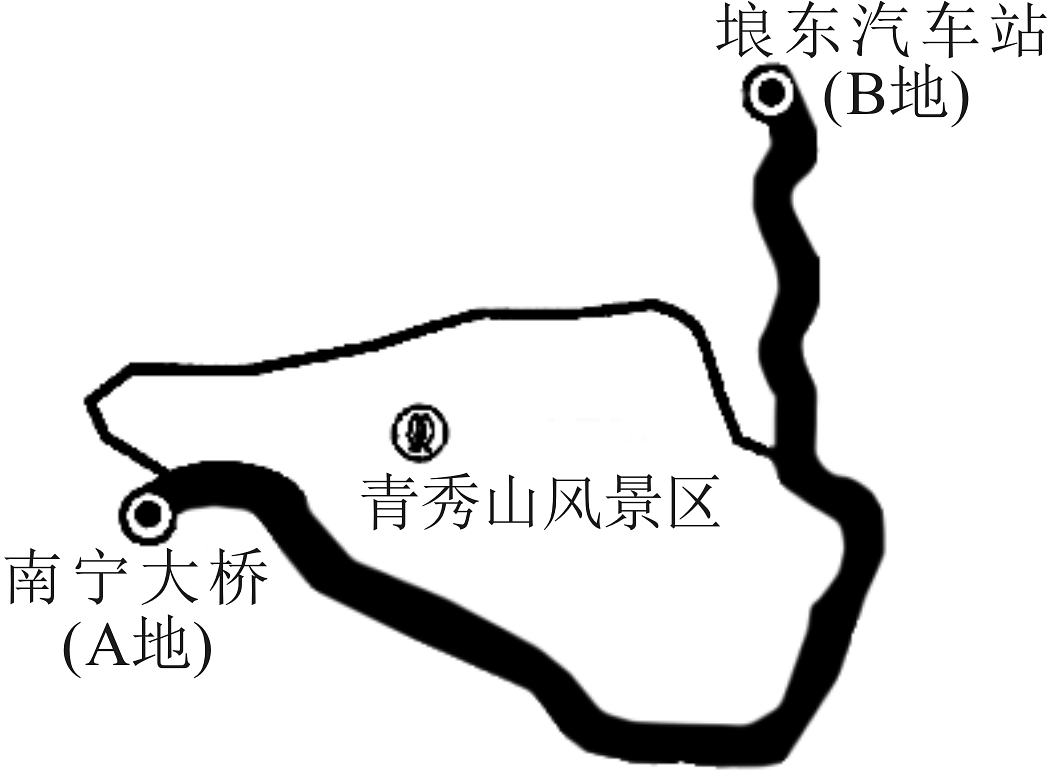
16. 解下列方程：

(1)、2(x+3)=5x；

(2)、 4x+3(2x-3)=12-(x+4)；

(3)、 $6 (\frac{1}{2} x - 4) + 2 x = 7 - (\frac{1}{3} x - 1);$

(4)、2-3(x+1)=1-2(1+0.5x).

查看试题解析
17. 南宁青环路起止于南宁大桥（A地）和埌东汽车站（B地），共约 $10 km$ ．周末，军军和壮壮两人相约去青环路骑行，军军从A地向B地骑行，平均速度是 $12 km / h$ ．军军出发 $20 \min$ 后，壮壮从B地向A地骑行，平均速度是 $15 km / h$ ．设军军骑行的时间为 $t h$ ．

(1)、用含 $t$ 的代数式分别表示两人骑行的路程；

(2)、当军军，壮壮相遇时，求 $t$ 的值；

(3)、两人相遇后，军军继续以原速度向B地骑行，壮壮休息 $2 \min$ 后掉头按原速度返回B地．在壮壮返回途中能否追上军军？请说明理由．

查看试题解析
18. 在“节能减排，做环保小卫士”的活动中，小明对两种照明灯的使用情况进行了调查，得出如下表所示的数据.已知这两种灯的照明效果一样，小明家所在地的电价是每度0.5元.(注：用电度数=功率(kW)×时间(h)，费用=灯的售价+电费)

功率/kW
使用寿命/h
价格/(元/盏)
白炽灯
0.1
2 000
3
节能灯
0.02
4 000
35

(1)、在白炽灯的使用寿命内，设照明时间为 xh，则一盏白炽灯的费用为元，一盏节能灯的费用为元.(用含x的式子表示)

(2)、在白炽灯的使用寿命内，当照明时间为多少时，使用这两种灯的费用相等?

(3)、如果计划照明4000 h，那么购买哪一种灯更省钱?请你通过计算说明理由.

查看试题解析
19. 2024 年，盲盒风潮依旧不减，各款盲盒层出不穷，让人眼花缭乱．镇海区某工厂共有 800名工人，负责生产 $A, B$ 两种盲盒。

(1)、若该工厂生产盲盒 $A$ 的人数比生产盲盒 $B$ 的人数的 3 倍少 200 人，请求出生产盲盒 $B$ 的工人人数；

(2)、为了促销，工厂按商家要求生产盲盒大礼包，该大礼包由 3 个盲盒 $A$ 和 4 个盲盒 $B$ 组成．已知每个工人平均每天可以生产 10 个盲盒 $A$ 或 20 个盲盒 $B$ ，且每天只能生产其中的一种盲盒．该工厂应该安排多少名工人生产盲盒 $A$ ，多少名工人生产盲盒 $B$ 才能使每天生产的盲盒正好配套？

查看试题解析

20. 平价商场经销的甲、乙两种商品，甲种商品每件售价60元，利润率为50％；乙种商品每件进价50元，售价80元

(1)、甲种商品每件进价为________元，每件乙种商品利润率为________；

(2)、若该商场同时购进甲、乙两种商品共50件，恰好总进价为2100元，求购进甲种商品多少件？

(3)、在“元旦”期间，该商场只对甲乙两种商品进行如下的优惠促销活动：

打折前一次性购物总金额	优惠措施
少于等于450元	不优惠
超过450元，但不超过600元	按售价打九折
超过600元	其中600元部分八点二折优惠，超过600元的部分打三折优惠

按上述优惠条件，若小华一次性购买乙种商品实际付款504元，求小华在该商场购买乙种商品多少件？

查看试题解析

21. 我们规定一种运算 $|\begin{matrix} a & b \\ c & d \end{matrix}| = a d - b c$ ，如 $|\begin{matrix} 3 & 4 \\ 5 & 6 \end{matrix}| = 3 \times 6 - 4 \times 5 = - 2$ ，按照这种运算规定，解答下列各题：

(1)、计算 $|\begin{matrix} - 5 & - 2 \\ 7 & 8 \end{matrix}| =$ ；

(2)、若 $|\begin{matrix} 2 x & 5 x \\ 3 & 4 \end{matrix}| - |\begin{matrix} 2 & 9 \\ - 3 x & - x \end{matrix}| = 8$ ，求x的值．

查看试题解析
22. 【背景知识】数轴是初中数学的一个重要工具，利用数轴可以将数与形完美地结合．研究数轴我们发现了许多重要的规律：若数轴上点 $A$ 、点 $B$ 表示的数分别为 $a$ 、 $b$ ，则 $A$ ， $B$ 两点之间的距离 $A B = |a - b|$ ，线段 $A B$ 的中点表示的数为 $\frac{a + b}{2}$ ．
【问题情境】如图，数轴上点 $A$ 表示的数为 $6$ ，点 $B$ 表示的数为 $- 4$ ，点 $P$ 从点 $A$ 出发，以每秒 $3$ 个单位长度的速度沿数轴向左匀速运动，同时点 $Q$ 从点 $B$ 出发，以每秒 $1$ 个单位长度的速度向右匀速运动．设运动时间为 $t$ 秒 $(t > 0)$ ．

(1)、【综合运用】
填空： $A$ 、 $B$ 两点间的距离 $A B =$ __________，线段 $A B$ 的中点 $C$ 表示的数为__________；

(2)、求当 $t$ 为何值时， $P Q = 2$ ；

(3)、若点 $M$ 为 $P A$ 的中点，点 $N$ 为 $P B$ 的中点，点 $P$ 在运动过程中，线段 $M N$ 的长度是否发生变化？若变化，请说明理由；若不变，请直接写出线段 $M N$ 的长．

查看试题解析
23. 【阅读材料】
我们知道“在数轴上表示的两个数，右边的数总比左边的数大”，利用此规律，我们可以求数轴上两个点之间的距离，具体方法是：用右边的数减去左边的数的差就是表示这两个数的两点之间的距离，若点M表示的数 $x_{1}$ ，点N表示的数是 $x_{2}$ ，点M在点N的右边（即 $x_{1} > x_{2}$ ），则点M，N之间的距离为 $x_{1} - x_{2}$ ，即 $M N = x_{1} - x_{2}$ ．例如：若点C表示的数是 $- 5$ ，点D表示的数是 $- 9$ ，则线段 $C D = - 5 - (- 9) = 4$ ．
【理解应用】
（1）已知在数轴上，点E表示的数是 $- 2024$ ，点F表示的数是 $2024$ ，求线段 $E F$ 的长；
【拓展应用】
如图，数轴上有三个点，点A表示的数是 $- 2$ ，点B表示的数是3，点P表示的数是x．
（2）当A，B，P三个点中，其中一个点是另外两个点所连线段的中点时，则 $x =$ __________；
（3）数轴上是否存在一点Q，使点Q到点A，点B的距离和为21？若存在，求出点Q表示的数；若不存在，请说明理由．

查看试题解析

	功率/kW	使用寿命/h	价格/(元/盏)
白炽灯	0.1	2 000	3
节能灯	0.02	4 000	35