北师大版数学九(上)第一章 特殊平行四边形 单元测试培优卷
试卷更新日期:2025-10-07 类型:单元试卷
一、选择题(每题5分,共50分)
-
1. 如图,将长方形绕其顶点B顺时针转到如图所示的位置,则旋转角可以为( )
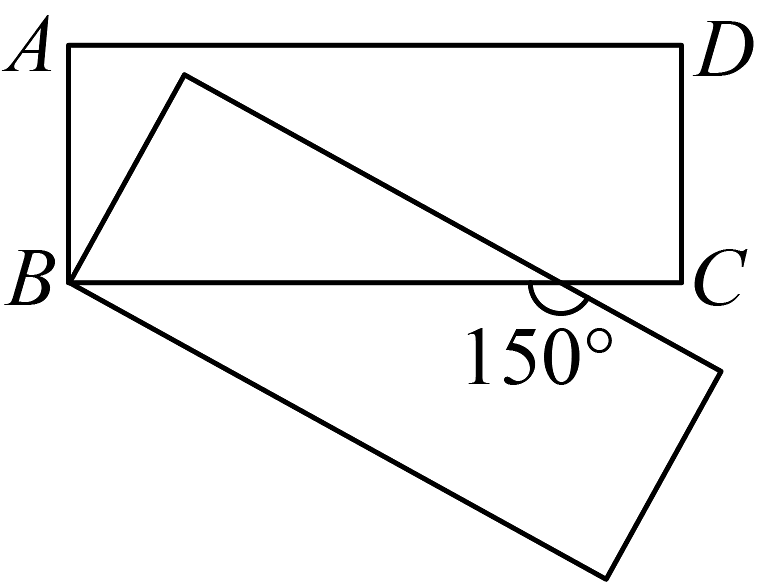 A、 B、 C、 D、2. 如图,已知四边形ABCD是平行四边形,下列说法正确的是( )
A、 B、 C、 D、2. 如图,已知四边形ABCD是平行四边形,下列说法正确的是( ) A、若 , 则是菱形 B、若 , 则是矩形 C、若 , 则是正方形 D、若 , 则是正方形3. 如图,在菱形中,分别是上的点,且与相交于点O.若 , 则的度数为( )
A、若 , 则是菱形 B、若 , 则是矩形 C、若 , 则是正方形 D、若 , 则是正方形3. 如图,在菱形中,分别是上的点,且与相交于点O.若 , 则的度数为( ) A、 B、 C、 D、4. 如图,将边长为的正方形折叠,使点落在边的中点处,点落在处,折痕为 , 则线段的长是( )
A、 B、 C、 D、4. 如图,将边长为的正方形折叠,使点落在边的中点处,点落在处,折痕为 , 则线段的长是( ) A、 B、 C、 D、5. 如图,由四个全等的直角三角形和小正方形拼成正方形 , 连接交于 . 若 , , 则的长为( )
A、 B、 C、 D、5. 如图,由四个全等的直角三角形和小正方形拼成正方形 , 连接交于 . 若 , , 则的长为( ) A、 B、 C、 D、6. 如图, , E为的中点,与相交于点F, , 则的度数是( )
A、 B、 C、 D、6. 如图, , E为的中点,与相交于点F, , 则的度数是( ) A、56° B、62° C、63° D、72°7. 如图,矩形的对角线和相交于点 , 平分交于点 , 如果 , 那么的度数为( )
A、56° B、62° C、63° D、72°7. 如图,矩形的对角线和相交于点 , 平分交于点 , 如果 , 那么的度数为( ) A、 B、 C、 D、8. 如图,在矩形中,点的坐标为 , 则的长是( )
A、 B、 C、 D、8. 如图,在矩形中,点的坐标为 , 则的长是( )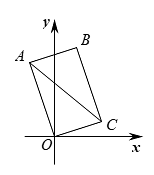 A、 B、 C、 D、9. 正方形 中,点 是 的中点,点 是 上异于点 的点, ,则 的值是( )
A、 B、 C、 D、9. 正方形 中,点 是 的中点,点 是 上异于点 的点, ,则 的值是( ) A、1 B、 C、 D、10. 如图,已知正方形的边长为4,P是对角线上一点,于点E,于点F,连接 . 给出下列结论:①;②四边形的周长为8:③一定是等腰三角形;④;⑤的最小值为;⑥ . 其中正确结论的序号为( )
A、1 B、 C、 D、10. 如图,已知正方形的边长为4,P是对角线上一点,于点E,于点F,连接 . 给出下列结论:①;②四边形的周长为8:③一定是等腰三角形;④;⑤的最小值为;⑥ . 其中正确结论的序号为( ) A、①②④⑤⑥ B、②③④⑤ C、①②④⑤ D、②④⑤⑥
A、①②④⑤⑥ B、②③④⑤ C、①②④⑤ D、②④⑤⑥二、填空题(每题5分,共25分)
-
11. 如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=10,BC=16,则EF的长为.
 12. 如图,在菱形纸片 中, 为 中点,折叠菱形纸片 ,使点 落在 所在的直线上,得到经过点 的折痕 . 则 的大小为度.
12. 如图,在菱形纸片 中, 为 中点,折叠菱形纸片 ,使点 落在 所在的直线上,得到经过点 的折痕 . 则 的大小为度. 13. 如图,四边形是菱形,对角线与相交于点 , , , 于点 , 则的长为 .
13. 如图,四边形是菱形,对角线与相交于点 , , , 于点 , 则的长为 . 14. 如图,菱形中, , , , 点P为对角线上的一个动点,则的最小值为 .
14. 如图,菱形中, , , , 点P为对角线上的一个动点,则的最小值为 .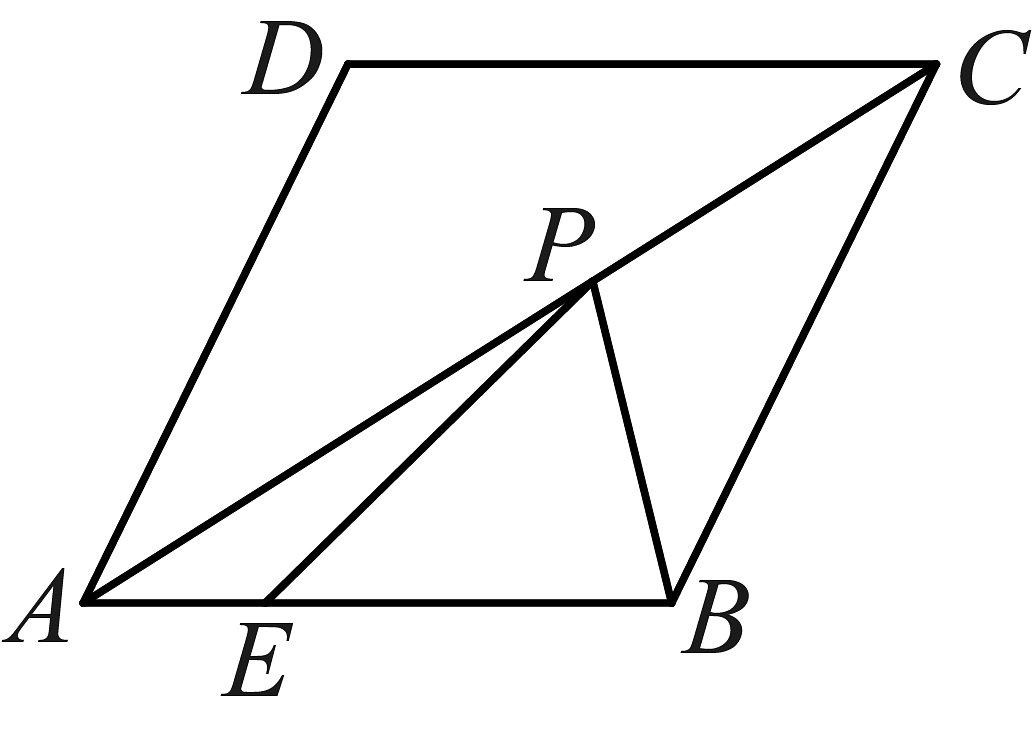 15. 如图,在矩形纸片中, , 为边的中点,点在边上,连接 , 将沿翻折,点的对应点为 , 连接 . 若 , 则 .
15. 如图,在矩形纸片中, , 为边的中点,点在边上,连接 , 将沿翻折,点的对应点为 , 连接 . 若 , 则 .
三、解答题(共8题,共75分)
-
16. 如图,在矩形中(),对角线相交于点O,延长到点E,使得 , 连接 , 点F是的中点,连接 .
 (1)、求证:四边形是菱形;(2)、若矩形的周长为20, , 求四边形的面积.17. 如图,在正方形中,点 , 分别在 , 上, , 垂足为 .
(1)、求证:四边形是菱形;(2)、若矩形的周长为20, , 求四边形的面积.17. 如图,在正方形中,点 , 分别在 , 上, , 垂足为 . (1)、求证:;(2)、若正方形的边长是8, , 点是的中点,求的长.18. 如图,在四边形中, , 分别是边上的点,连接交于点 , . 添加下列条件之一使四边形成为菱形:①;② .
(1)、求证:;(2)、若正方形的边长是8, , 点是的中点,求的长.18. 如图,在四边形中, , 分别是边上的点,连接交于点 , . 添加下列条件之一使四边形成为菱形:①;② . (1)、你添加的条件是______(填序号),并证明.(2)、在(1)的条件下,连接 , 若 , 求菱形的面积.19. 在中,于点D,点E是边的中点,过A作交的延长线于点F,连接 .
(1)、你添加的条件是______(填序号),并证明.(2)、在(1)的条件下,连接 , 若 , 求菱形的面积.19. 在中,于点D,点E是边的中点,过A作交的延长线于点F,连接 . (1)、如图1,求证:四边形是矩形.(2)、如图2,当时,取中点G,连接 , 在不添加任何辅助线的情况下,请直接写出图中所有面积为矩形面积一半的平行四边形.20. 如图,在两个等腰直角和中, , 点M为中点,点N为中点.
(1)、如图1,求证:四边形是矩形.(2)、如图2,当时,取中点G,连接 , 在不添加任何辅助线的情况下,请直接写出图中所有面积为矩形面积一半的平行四边形.20. 如图,在两个等腰直角和中, , 点M为中点,点N为中点. (1)、观察猜想:
(1)、观察猜想:如图1,点E在上,线段与的数量关系是______,位置关系是______;
(2)、探究证明:把绕直角顶点C旋转到图2的位置,(1)中的结论还成立吗?说明理由;
(3)、拓展延伸:把绕点C在平面内自由旋转,若 , , 当A、D、E三点处于同一条直线上时,请直接写出AM的长.
21. 阅读以下材料,并按要求完成相应的任务:从正方形的一个顶点引出夹角为的两条射线,并连接它们与该顶点的两对边的交点构成的基本平面几何模型称为半角模型.半角模型可证出多个几何结论,例如:
如图1,在正方形中,以为顶点的 , 、与、边分别交于、两点.易证得: .
大致证明思路:如图2,将绕点顺时针旋转 , 得到 , 由可得、、三点共线, , 进而可证明 , 故 .
任务:

如图3,在四边形中, , , , 以为顶点的 , 、与、边分别交于、两点.请参照阅读材料中的解题方法,你认为结论是否依然成立,若成立,请写出证明过程;若不成立,请说明理由.
22. (1)、【阅读发现】
(1)、【阅读发现】如图1,在正方形ABCD的外侧作等边三角形.ABE和等边三角形ADF,连结ED与FC相交于点M,则图中△ADE≌△DFC,可知DE=FC,并可求得∠DMC=°.
(2)、【拓展应用】如图2,在矩形ABCD(AB>BC)的外侧作等边三角形ABE和等边三角形ADF,连结ED与FC相交于点M.
求证:DE=FC.
(3)、若∠ADE=20°,求∠DMC的度数.23. 【模型建立】
(1)如图1,已知和 , , , , . 用等式写出线段 , , 的数量关系,并说明理由.
【模型应用】
(2)如图2,在正方形中,点E,F分别在对角线和边上, , . 用等式写出线段 , , 的数量关系,并说明理由.
【模型迁移】
(3)如图3,在正方形中,点E在对角线上,点F在边的延长线上, , . 用等式写出线段 , , 的数量关系,并说明理由.