北师大版数学九(上)第一章 特殊平行四边形单元测试基础卷
试卷更新日期:2025-10-07 类型:单元试卷
一、选择题(每题5分,共50分)
-
1. 下列说法正确的是( )A、菱形的四个内角都是直角 B、矩形的对角线互相垂直 C、正方形的每一条对角线平分一组对角 D、平行四边形是轴对称图形2. 如图,在矩形中,对角线与相交于点 , 则下列结论一定正确的是( )
 A、 B、 C、 D、3. 已知四边形是平行四边形,与相交于点O,下列结论正确的有( )
A、 B、 C、 D、3. 已知四边形是平行四边形,与相交于点O,下列结论正确的有( )①当时,它是菱形;②时,它是菱形;③当时,它是矩形;④当时,它是正方形.
A、4个 B、3个 C、2个 D、1个4. 如图,在一个对边平行的纸条上有两点A , B及线段AB的中点O , 以下操作和判断不正确的是( )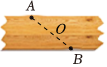 A、过点O作任意直线(除直线AB)交纸条两边于点C , D , 得到平行四边形ACBD B、过点O作AB的垂线l交纸条两边于点C , D , 得到菱形ACBD C、分别过点A , B作对边的垂线,交对边于点C , D , 得到矩形ACBD D、在点A , B所在边的对边分别取C , D两点,使得AC=BD , 得到平行四边形ACBD5. 如图,直线 , 矩形的顶点A在直线b上,若 , 则的度数为( )
A、过点O作任意直线(除直线AB)交纸条两边于点C , D , 得到平行四边形ACBD B、过点O作AB的垂线l交纸条两边于点C , D , 得到菱形ACBD C、分别过点A , B作对边的垂线,交对边于点C , D , 得到矩形ACBD D、在点A , B所在边的对边分别取C , D两点,使得AC=BD , 得到平行四边形ACBD5. 如图,直线 , 矩形的顶点A在直线b上,若 , 则的度数为( ) A、 B、 C、 D、6. 如图,在矩形中,对角线 , 相交于点O,若 , 则的长为( )
A、 B、 C、 D、6. 如图,在矩形中,对角线 , 相交于点O,若 , 则的长为( ) A、3 B、4 C、5 D、67. 如图,四边形是正方形,延长到点E,使 , 连结交于点F,则等于( )度.
A、3 B、4 C、5 D、67. 如图,四边形是正方形,延长到点E,使 , 连结交于点F,则等于( )度.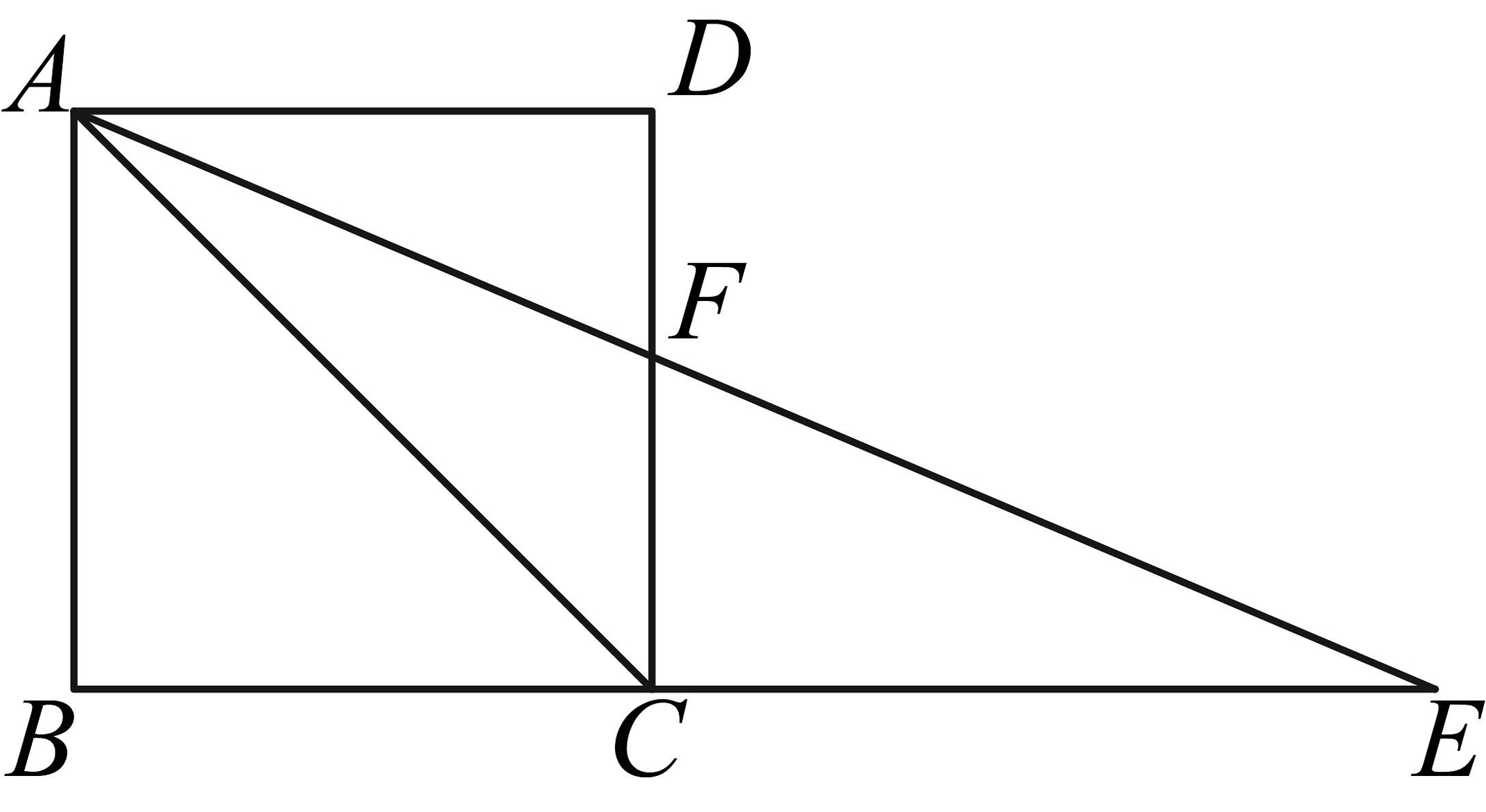 A、112.5 B、125 C、135 D、1508. 如图,在正方形中, , E,F分别为边的中点,连接 , 点G,H分别为的中点,连接 , 则的长为( )
A、112.5 B、125 C、135 D、1508. 如图,在正方形中, , E,F分别为边的中点,连接 , 点G,H分别为的中点,连接 , 则的长为( ) A、 B、1 C、 D、29. 如图,正方形 ABCD 中,已知 , 对角线 AC 与 BD 交于点 O,点 E 为射线 OB 上的一个动点(不与点 B 重合),点 M 为线段 ED 的中点. 现将线段 OM 绕点 M 顺时针旋转 得到线段 MF,连结 AE, EF, AF, OF. 在点 E 的运动过程中,当 时,则线段 BE 的长为( )
A、 B、1 C、 D、29. 如图,正方形 ABCD 中,已知 , 对角线 AC 与 BD 交于点 O,点 E 为射线 OB 上的一个动点(不与点 B 重合),点 M 为线段 ED 的中点. 现将线段 OM 绕点 M 顺时针旋转 得到线段 MF,连结 AE, EF, AF, OF. 在点 E 的运动过程中,当 时,则线段 BE 的长为( ) A、 B、 C、 或 D、 或
A、 B、 C、 或 D、 或二、填空题(每题5分,共25分)
-
10. 如图,在平面直角坐标系中,点A的坐标为 , 点C的坐标为 . 以为边作矩形 , 若将矩形绕点O顺时针旋转 , 得到矩形 , 则点的坐标为 .
 11. 如图,在菱形中,点O为对角线的交点,且在内, , , 则菱形两对边的距离 .
11. 如图,在菱形中,点O为对角线的交点,且在内, , , 则菱形两对边的距离 . 12. 如图,点在正方形内部,且是等边三角形,连接、 , 则 .
12. 如图,点在正方形内部,且是等边三角形,连接、 , 则 . 13. 如图,菱形中, , 面积为60,对角线AC与BD相交于点O,过点A作 , 交边于点E,连接 , 则 .
13. 如图,菱形中, , 面积为60,对角线AC与BD相交于点O,过点A作 , 交边于点E,连接 , 则 .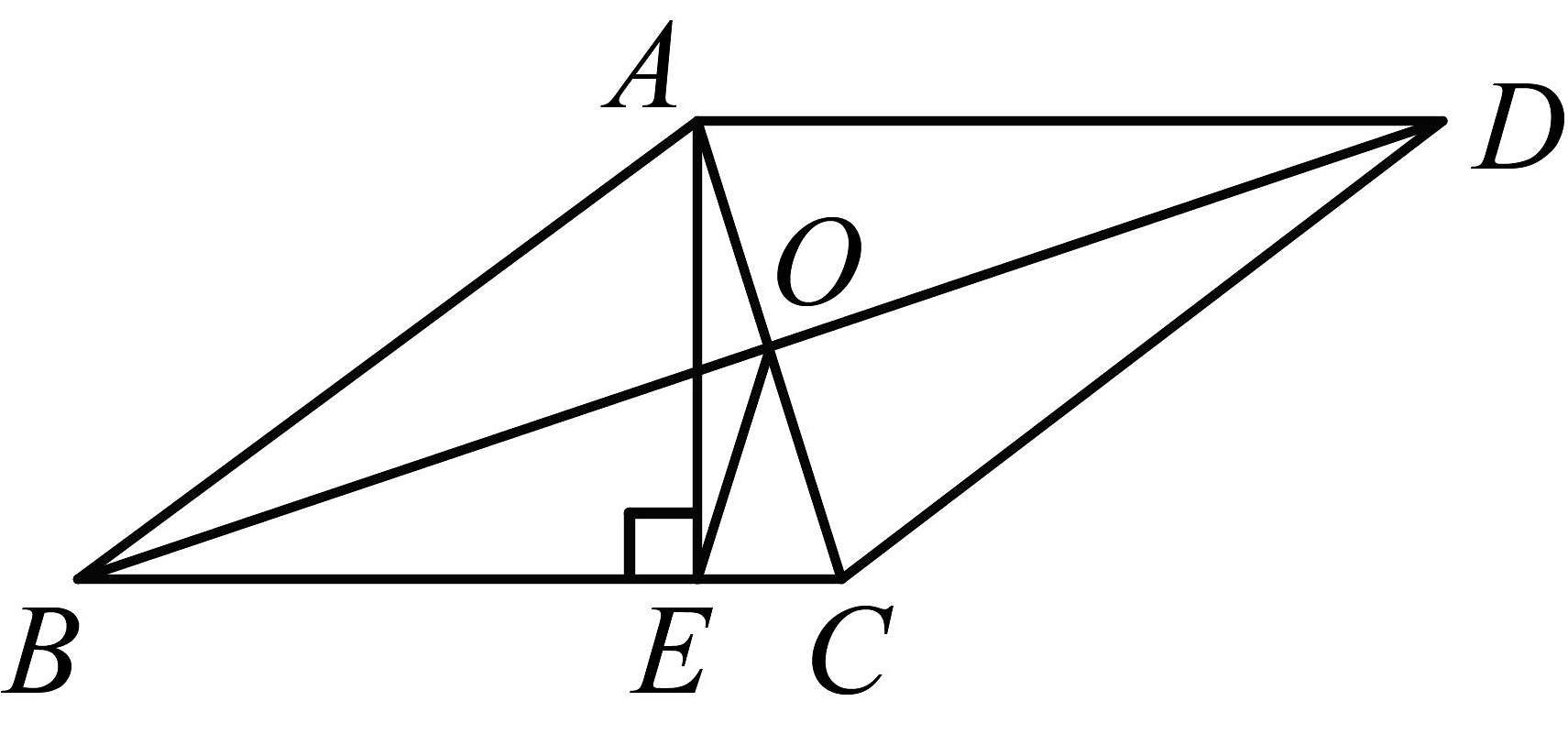 14. 如图,矩形中,点E在边上,将矩形沿直线折叠,点A恰好落在边的点F处.若 , , 则的长是 .
14. 如图,矩形中,点E在边上,将矩形沿直线折叠,点A恰好落在边的点F处.若 , , 则的长是 .
三、解答题(共8题,共75分)
-
15. 如图,的对角线AC、BD相交于点O , , OE与AB交于点F .
 (1)、在不添加新的点和线的前提下,增加一个条件: ▲ , 使得四边形AOBE是矩形,并说明理由;(2)、若 , 求的面积.16. 如图所示,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF , 连接EF , BF , EF与对角线AC交于点O , 且BE=BF , ∠BEF=2∠BAC .
(1)、在不添加新的点和线的前提下,增加一个条件: ▲ , 使得四边形AOBE是矩形,并说明理由;(2)、若 , 求的面积.16. 如图所示,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF , 连接EF , BF , EF与对角线AC交于点O , 且BE=BF , ∠BEF=2∠BAC . (1)、求证:OE=OF;(2)、若BC=2
(1)、求证:OE=OF;(2)、若BC=2 , 求AB的长. 17. 如图,在中, , E为CA延长线上一点,D为AB上一点,F为外一点且连接DF,BF.
, 求AB的长. 17. 如图,在中, , E为CA延长线上一点,D为AB上一点,F为外一点且连接DF,BF.
(1)当的度数是多少时,四边形ADFE为菱形,请说明理由:
(2)当AB= 时,四边形ACBF为正方形(请直接写出)
18. 已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,BE⊥AC于E,CF⊥BD于F,请你判断BE与CF的大小关系,并说明你的理由. 19. 如图,方格纸中每个小正方形的边长均为1,我们把每个小正方形的顶点叫做格点. 如:线段AB的两个端点都在格点上.
19. 如图,方格纸中每个小正方形的边长均为1,我们把每个小正方形的顶点叫做格点. 如:线段AB的两个端点都在格点上.(1)在图1中画一个以AB为边的平行四边形ABCD,点C、D在格点上,且平行四边形ABCD的面积为15;
(2)在图2中画一个以AB为边的菱形ABEF(不是正方形),点E、F在格点上,则菱形ABEF的对角线AE=________,BF=________;
(3)在图3中画一个以AB为边的矩形ABMN(不是正方形),点M、N在格点上,则矩形ABMN的长宽比=______.
 20. 已知:如图,点E是正方形的边上一点, , , 逆时针旋转后能够与重合..
20. 已知:如图,点E是正方形的边上一点, , , 逆时针旋转后能够与重合.. (1)、旋转中心是_________,旋转角为_________度;(2)、请你判断的形状,并说明理由.21. 如图,在直角坐标系中,是等腰直角三角形,斜边在x轴上,且点B的坐标是 , 直线经过点A,且分别与x轴、y轴交于D、C两点,以为边在第一象限内作正方形 .
(1)、旋转中心是_________,旋转角为_________度;(2)、请你判断的形状,并说明理由.21. 如图,在直角坐标系中,是等腰直角三角形,斜边在x轴上,且点B的坐标是 , 直线经过点A,且分别与x轴、y轴交于D、C两点,以为边在第一象限内作正方形 . (1)、求点A的坐标和k的值;(2)、求直线所对应的函数关系式.22. 【阅读理解】
(1)、求点A的坐标和k的值;(2)、求直线所对应的函数关系式.22. 【阅读理解】半角模型是指有公共顶点,锐角等于较大角的一半,且组成这个较大角的两边相等.通过旋转或截长补短,将角的倍分关系转化为角的相等关系,并进一步构成全等三角形,用以解决线段关系、角度、面积等问题,
【初步探究】
如图1,在正方形中,点分别在边上,连接 . 若 , 将绕点顺时针旋转 , 点与点重合,得到 . 易证: .
(1)根据以上信息,填空:
①_______°;
②线段之间满足的数量关系为_______;
【迁移探究】
(2)如图2,在正方形中,若点在射线上,点在射线上, , 猜想线段之间的数量关系,请证明你的结论;
【拓展探索】
(3)如图3,已知正方形的边长为 , 连接分别交于点 , 若点恰好为线段的三等分点,且 , 求线段的长.
