4.3《 一次函数的图象》（4）—北师版数学八年级上册课堂分层训练
试卷更新日期：2025-10-06 类型：同步测试
一、基础夯实
-
1. 甲、乙两个草莓采摘园为吸引顾客，在草莓销售价格相同的基础上分别推出优惠方案，甲园：顾客进园需购买门票，采摘的草莓按六折优惠．乙园：顾客进园免门票，采摘草莓超过一定数量后，超过的部分打折销售．活动期间，某顾客的草莓采摘量为x千克，若在甲园采摘需总费用y1元，若在乙园采摘需总费用y2元．y1 ， y2与x之间的函数图象如图所示，则下列说法中错误的是（ ）
A、甲园的门票费用是60元 B、草莓优惠前的销售价格是40元/千克 C、乙园超过5千克后，超过的部分价格优惠是打五折 D、若顾客采摘15千克草莓，那么到甲园比到乙园采摘更实惠2. 甲、乙两辆摩托车分别从A、B两地出发相向而行，图中 、 分别表示两辆摩托车与A地的距离s（千米）与行驶时间t（小时）之间的函数关系，则下列说法：
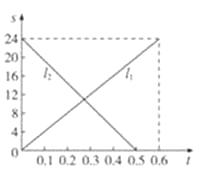
①A、B两地相距24千米；
②甲车比乙车行完全程多用了0.1小时；
③甲车的速度比乙车慢8千米／时；
④两车出发后，经过 小时，两车相遇．
其中正确的有（ ）
A、1个 B、2个 C、3个 D、4个3. 在一次800米的长跑比赛中，甲、乙两人所跑的路程s(米)与各自所用的时间t(秒)之间的函数图象分别为图中的线段 OA 和折线O-B-C-D，则下列说法正确的是( )
A、甲的速度随着时间的增大而增大 B、乙的平均速度比甲的平均速度大 C、在起跑后第180秒时，两人相遇 D、在起跑后第50秒时，乙在甲的前面4. 甲、乙两位同学骑自行车，从各自家出发上学，他们离乙家的距离y(km)与出发时间x(min)之间的函数关系如图所示，则乙比甲早到分钟．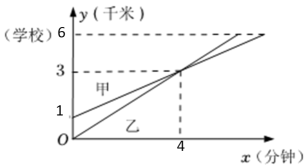
5. 甲、乙二人从学校出发去科技馆，甲步行一段时间后，乙骑自行车沿相同路线行进，两人均匀速前行，他们的路程差s（米）与甲出发时间t（分）之间的函数关系如图所示．下列说法：①乙先到达青少年宫；②乙的速度是甲速度的2.5倍；③b＝480；④a＝24．其中正确的是（填序号）.
6. 生物活动小组的同学们观察某植物的生长情况，得到该植物的高度y(cm)与观察时间x(天)的关系，画出如图所示的函数图象(CD∥x 轴)，则该植物最高长到 cm.
7. 某水果店销售某种水果，销售额y（元）与一次销售量与之间的函数关系如图所示．若王叔叔从该水果店一次性购买该种水果，需要付款元．
8. 已知A，B两地相距80km，甲、乙两人沿同一条公路从A地出发到B地，甲骑摩托车，乙骑自行车。图中DE，OC分别表示甲、乙离开A地的路程s(km)与乙离开A地的时间t(h)的函数关系的图象，根据图象填空。
(1)、乙先出发，甲后出发，相差h。(2)、大约在乙出发后h两人相遇，相遇地点离开A地km。(3)、甲到达B地时，乙在离A地约km处。(4)、甲的速度为 ， 乙的速度为。(5)、乙离开A地的路程s(km)关于时间t(h)的函数表达式为。(6)、甲离开A地的路程s(km)关于时间t(h)的函数表达式为。9. 一慢车和一快车沿相同路线从A地到相距120千米的B地，所行地路程与时间的函数图象如图所示．试根据图象，回答下列问题：
(1)、慢车比快车早出发小时，快车比慢车少用小时到达B地；(2)、快车用了多少时间追上慢车；此时距离A地多少千米？(3)、慢车行驶多少小时两车相距10km.10. 某长途汽车客运站规定，乘客可以免费携带一定质量的行李，但超过该质量则须交纳行李费，已知行李费y（元）是行李质量x（千克）的一次函数现在刘明带了60千克的行李，交了行李费5元，王华带了90千克的行李，交了行李费10元.(1)、求y与x之间的函数关系式；(2)、旅客可以免费携带多少千克的行李？二、能力提升
-
11. 快车从甲地匀速开往乙地，慢车从乙地出发沿同一条公路匀速前往甲地.慢车先出发1小时，快车再出发.设慢车行驶的时间为小时，两车之间的距离为千米，与的函数关系如图所示.下列结论：①快车出发4.4小时后两车相遇；②慢车的速度是100千米／小时；③线段AB所在直线的函数表达式为 ， 正确的有（ ）
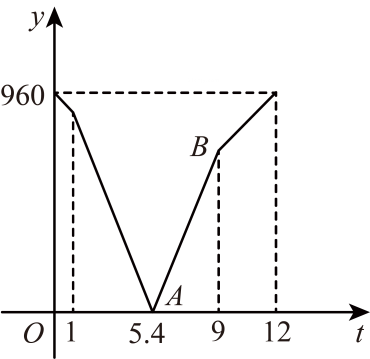A、①② B、②③ C、①②③ D、①③12. 甲、乙两人沿同一跑道从A处跑到B处。乙比甲先出发2分钟，甲的速度为每分钟150米。若两人之间的路程y（米）与甲出发的时间x（分钟）的关系如图所示，则A、B两地的路程为（ ）
A、1800米 B、2000米 C、2400米 D、2500米13. 第一次“龟兔赛跑”，兔子因为在途中睡觉而输掉比赛，很不服气，决定与乌龟再比一次，并且骄傲地说，这次我一定不睡觉，让乌龟先跑一段距离我再去追都可以赢.结果兔子又一次输掉了比赛.下列函数图象可以体现这次比赛过程的是( ).A、
B、
C、
D、
14. “漏刻”是我国古代一种利用水流计时的工具（如图1），综合实践小组用甲、乙两个透明的竖直放置的容器和一根装有节流阀（控制水的流速）的软管，制作了类似“漏刻”的简易计时装置（如图2）。上午9：00，综合实践小组在甲容器里加满水，经过实验得到甲容器的水面高度h（cm）与流水时间t（min）的关系如图3所示，下列说法错误的是（ ）
A、甲容器的初始水面高度为30cm； B、14：00甲容器的水流光； C、甲容器的水面高度h与流水时间t的关系式为； D、11：00时甲容器的水面高度为12cm。15. 在某公用电话亭打电话时，需付电话费y（元）与通话时间 x（分钟）之间的函数关系用图象表示如图．则小明打了6分钟需付费元．
16. 已知A，B两地相距 ， 甲、乙两人沿同一条公路从A地出发到B地（先到达B地者在终点等待），甲骑摩托车，乙骑自行车．图中分别表示甲、乙离开A地的路程s（）与时间t（h）的函数关系的图象（如图），则当两人之间的路程超过时，时间t的取值范围是 ．
17. 如图1，11月10日晚，“深爱万物”—2023深圳人才嘉年华活动正式启动，千余架无人机在深圳人才公园上空上演“天空之舞”，为人才喝彩、向人才致敬．如图2的平面直角坐标系中，线段分别表示1号、2号无人机在队形变换中飞行高度 ， 与飞行时间的函数关系，其中 ， 线段与相交于点P，轴于点B，点A的横坐标为25．则在第秒时1号和2号无人机在同一高度．
18. 已知甲、乙两个仓库分别有物资800 吨和1200 吨，现要把这些物资全部运往A，B 两地，A 地需要物资1300 吨，B地需要物资700吨，从甲、乙两仓库把物资运往A，B两地的运费单价如下表：A地(元/吨)
B地(元/吨)
甲仓库
12
15
乙仓库
10
18
(1)、设甲仓库运往A 地 x吨物资，直接写出总运费y(元)关于x(吨)的函数表达式(不需要写出自变量的取值范围)；(2)、当甲仓库运往A 地多少吨物资时，总运费最少?总运费最少是多少?(3)、若甲仓库运往 A 地的运费下降了 a 元/吨后(2≤a≤6且a为常数)，最少的总运费为23 100元，求a 的值.19. 某公司每月生产A，B两种型号的口罩共20万只，且所有口罩当月全部售出。两种型号口罩的成本、售价如下表。口罩型号
每只成本/元
每只售价/元
A
1
1.5
B
3
6
(1)、设该公司每月生产A型口罩x万只，月毛利润为y万元，试写出y关于x的函数表达式。(2)、该公司计划5月投入口罩生产的成本不超过28万元，且B型口罩每只售价降低2元，问：应该怎样安排A，B两种型号口罩的产量，使得当月销售毛利润最大?并求出最大毛利润。20. 汽车出发前油箱内有油50L，行驶一段时间在加油站加油若干升.汽车出发后，油箱中的剩余油量y(单位：L)与行驶时间t(单位：h)之间的关系如图所示.
(1)、汽车行驶h在加油站加油L.(2)、求加油前油箱中剩余油量y与行驶时间t之间的关系式.(3)、如果加油前、加油后汽车都以70km/h的速度匀速行驶，加油站距离目的地210km，那么要到达目的地，油箱中的油是否够用?请说明理由.三、综合拓展
-
21. 一辆客车从甲地开往乙地，一辆出租车从乙地开往甲地，两车同时出发．设客车与甲地的距离为（千米），出租车与甲地的距离为（千米），两车行驶的时间为x（小时），、与x的函数关系图象如图所示：
(1)、根据图象，直接写出、与x的函数表达式，并写出相应的自变量取值范围．(2)、运用（1）的结论，求当时两车之间的距离．(3)、若在出租车到达甲地之前，两车间的距离为S，求S与x的函数表达式．22. 某医药研究所开发了一种新药，在实验药效时发现，如果按规定剂量服用，每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示，那么当按规定剂量服药后，根据图象回答下列问题：
(1)、当时，求关于的函数关系式．(2)、当时，求关于的函数关系式．(3)、如果每毫升血液中含药量为微克或微克以上时治疗疾病最有效，求这个有效时间的范围．