4.3《 一次函数的图象》（3）—北师版数学八年级上册课堂分层训练
试卷更新日期：2025-10-06 类型：同步测试
一、基础夯实
-
1. 某公司市场营销部的个人月收入与其每月的销售量成一次函数关系，其图像如图所示，由图中给出的信息可知，营销人员没有销售时的收入是( )
A、310元 B、300元 C、290元 D、280元2. 如图，一次函数与的图象相交于点A，则点A的坐标为（ ）
A、 B、 C、 D、3. 直线y＝﹣3x与y＝﹣3x＋15的位置关系是（ ）A、重合 B、平行 C、相交 D、无法判断4. 同一温度的华氏度数（℉）与摄氏度数（℃）之间的函数关系是 ， 如果某一温度的摄氏度数是5℃，那么它的华氏度数是℉．5. 在弹性限度内，弹簧的长度y cm与所挂物体的质量x kg之间是一次函数关系，其图象如图所示，则弹簧本身的长度为 ．
6. 元旦期间，胡老师开车从扬州到相距150千米的老家探亲，如果油箱里剩余油量 y（升）与行驶里程 x（千米）之间是一次函数关系，其图象如图所示，那么胡老师到达老家时，油箱里剩余油量是升．
7. 如图，把一些相同规格的碗整齐地叠放在水平桌面上，这摞碗的高度随着碗的数量变化而变化的情况如表格所示：碗的数量（只） 1 2 3 4 5 ······ 高度（cm） 4 5.2 6.4 7.6 8.8 ······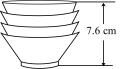 
(1)、上述两个变量之间的关系中，哪个是自变量？哪个是因变量？(2)、用h（cm）表示这摞碗的高度，用（只）表示这摞碗的数量，请用含有的代数式表示h；(3)、若这摞碗的高度为11.2cm，求这摞碗的数量.8. 甲、乙两辆汽车分别从A、B两地同时出发，沿同一条公路相向而行，乙车车发2h后休息，与甲车相遇后，继续行驶，设甲、乙两车与B地的路程分别为y甲（km），y乙（km），甲车行驶的时间为x（h），y甲 ， y乙与x之间的函数图象如图所示，结合图象解答下列问题：
(1)、求：y甲与x的函数关系式，并写出自变量x的取值范围；(2)、乙车休息了h；(3)、当两车相距80km时，直接写出x的值．二、能力提升
-
9. 如图，小明骑自行车从甲地到乙地，折线表示小明途中行程s(km)与所花时间t(h)之间的函数关系.出发后5小时，小明离甲地千米.
10. 一家游泳馆的游泳收费标准为30元/次，若购买会员年卡，可享受如下优惠：会员年卡类型
办卡费用（元）
每次游泳收费（元）
A 类
50
25
B 类
200
20
C 类
400
15
例如，购买A类会员年卡，一年内游泳20次，消费50+25×20=550元，若一年内在该游泳馆游泳的次数介于45～55次之间，则最省钱的方式为（ ）
A、购买A类会员年卡 B、购买B类会员年卡 C、购买C类会员年卡 D、不购买会员年卡11. 某快递公司每天上午8：00~9：00为集中揽件和派件时段，甲仓库用来揽收快件，乙仓库用来派发快件，该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示，那么当两仓库快递件数相同时，此刻的时间为( )
A、8：10 B、8：15 C、8：20 D、8：2512. 如图，购买一种苹果所付款金额y（元）与购买量x（千克）之间的函数图象由线段和射线组成，则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省（ ）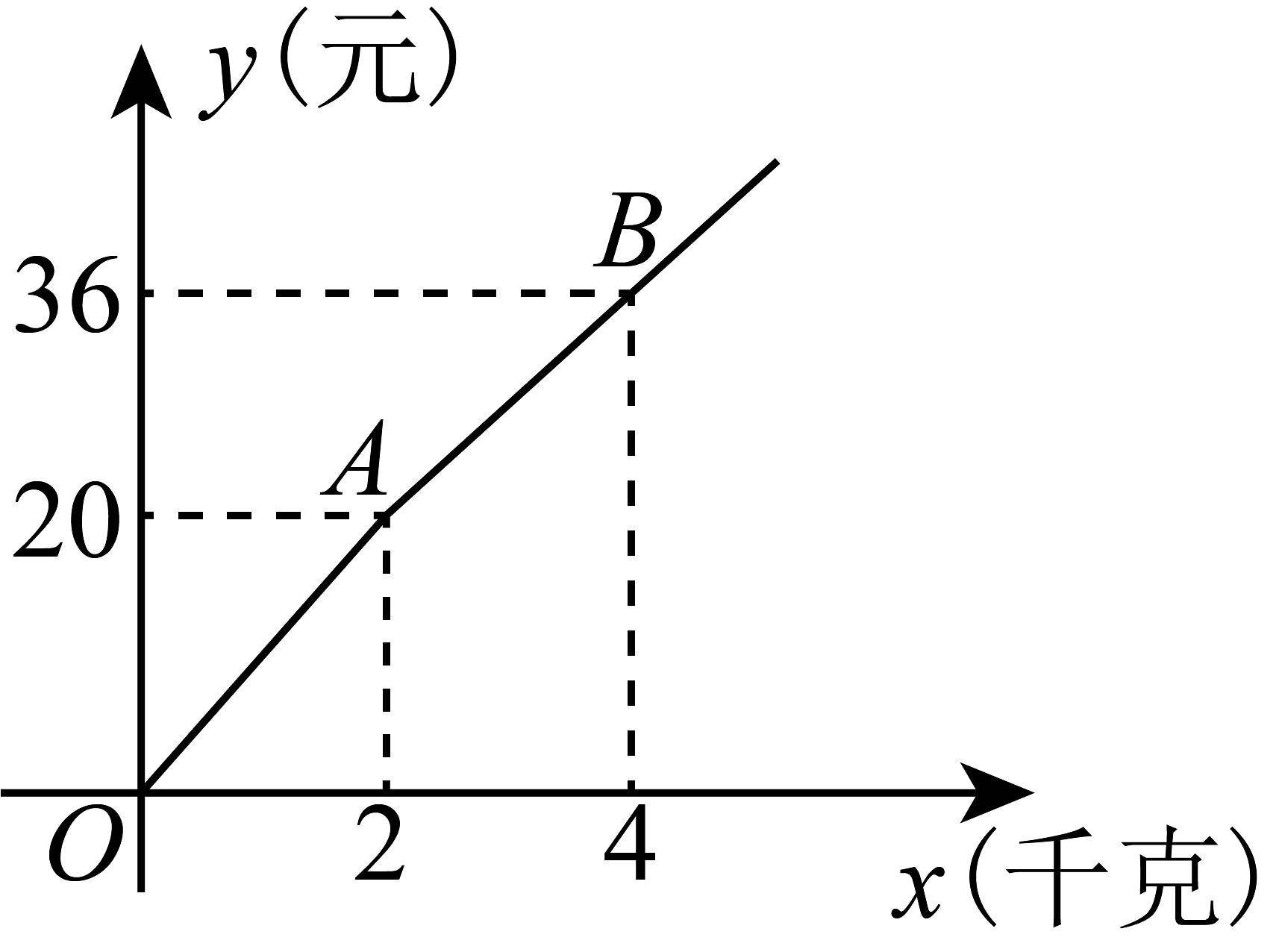
A、4元 B、3元 C、2元 D、1元13. 如图所示，反映了天利公司某种产品的销售收入与销售量的关系，反映了该种产品的销售成本与销售量的关系．根据图象提供信息，下列说法正确的是（ ）
A、当销售量为2吨时，销售成本是2000元 B、销售成本是5000元时，该公司的该产品盈利 C、当销售量为5吨时，该公司的该产品盈利1000元 D、的函数表达式为14. 如图所示，购买一种苹果，所付款金额y（元）与购买量x（千克）之间的函数图象由线段OA和射线AB组成，则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省 元．
15. 科学家研究发现，声音在空气中传播的速度y(米/秒)与气温x(℃)有关，它们之间的关系如下表所示：气温/℃
…
0
5
10
15
20
…
速度/(米/秒)
…
331
334
337
340
343
…
(1)、气温每上升5℃，声音在空气中传播的速度就增加米/秒．(2)、直接写出y与x的关系式：.(3)、当声音在空气中传播的速度为403米/秒时，气温x=℃．16. 某医药研究所开发了一种新药，在实验药效时发现，如果成人按规定剂量服用，每毫升血液中含药量y（微克）随时间x（时）的变化情况如图所示，那么当成人按规定剂量服药后，根据图象回答下列问题：
(1)、服药后小时，血液中含药量最高，达每毫升微克，接着逐步衰减．(2)、服药后5小时，血液中含药量为每毫升微克．(3)、当x≤2时，y关于x的函数表达式是(4)、当2≤x≤8时，y关于x的函数表达式是 ．(5)、如果每毫升血液中含药量为3微克或3微克以上时治疗疾病最有效，那么这个有效时间范围是时．17. 某超市最近销售蓝莓，根据以往的销售经验，每天的售价与销售量之间有如下关系：每千克售价（元）
60
59
58
57
56
……
30
每天销售量（千克）
50
55
60
65
70
……
200
(1)、表格中的自变量是 ， 因变量是 ．(2)、设当售价从每千克60元下降了x元时，每天销售量为y千克，直接写出y与x之间的关系式；(3)、如果周六的销售量是170千克，那这天的售价是每千克多少元？(4)、如果蓝莓的成本价是30元/千克，某天的售价定为40元/千克，当天的销售利润是多少？18. 工厂某车间需加工一批零件，甲组工人加工中因故障产检修机器一次，然后以原来的工作效率继续加工，由于时间紧任务重，乙组工人也加入共同加工零件。设甲组加工时间t（时），甲组加工买件的数量为y甲个。乙组加工数量为y乙个，其函数图象如图所示：
(1)、求 乙与 之间的函数关系式，并写出 的取值范围；(2)、求 的值，并说明 的实际意义；(3)、甲组加工多长时间时，甲，乙两组加工夆件的总数为 480 个．三、综合拓展
-
19. 甲、乙两人相约周末登花果山，甲、乙两人距地面的高度y（米）与登山时间x（分）之间的函数图象如图所示，根据图象所提供的信息解答下列问题：
(1)、甲登山上升的速度是每分钟米，乙在A地时距地面的高度b为米；(2)、若乙提速后，乙的登山上升速度是甲登山上升速度的3倍，请求出乙登山全程中，距地面的高度y（米）与登山时间x（分）之间的函数关系式．(3)、登山多长时间时，甲、乙两人距地面的高度差为50米？20. 某游泳池的平面图如图1，宽30米，深水区长40米，浅水区长8米.游泳池应定期换水.图2是小明给游泳池放水时，游泳池的存水量Q（立方米）与放水时间t（小时）的函数图象.其中表示正好放到浅水区底部时的状态.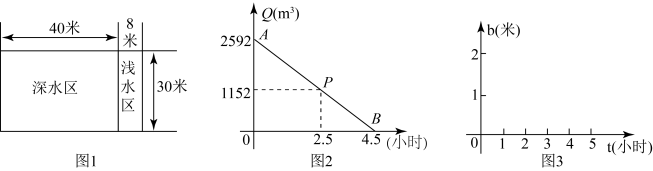
(1)、观察图1，图2.可知：深水区的面积是平方米，浅水区的面积是平方米，放水速度是每小时立方米；(2)、求Q关于t的函数表达式，并写出自变量t的取值范围；(3)、游泳池清理干净后，又将水放到原来的高度.若进水速度与放水速度相同，请在图3中，画出游泳池中的水深h（米）关于进水时间t（小时）的函数图象（请标注关键点的坐标）.