人教版八(上)数学第十三章 三角形 单元测试培优卷
试卷更新日期:2025-09-30 类型:单元试卷
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1. 木工师傅要做一个三角形木架,有两根木条的长度为7cm和14cm,第三根木条的长度可以是( )A、5cm B、18cm C、21cm D、23cm2. 如图,在中, , , D是BC边上的一点,若的周长比的周长大2,则AD是( )
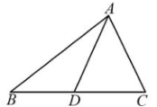 A、的高 B、的角平分线 C、的中线 D、都有可能3. 如图,在 中,外角 ,则 的度数为( )
A、的高 B、的角平分线 C、的中线 D、都有可能3. 如图,在 中,外角 ,则 的度数为( ) A、 B、 C、 D、4. 有4根长度分别为2、4、6、7的木条,从中任意选出三根,其中能构成三角形的有( )A、1种 B、2种 C、3种 D、4种5. 如图,AD是△ABC的角平分线,AC∥DE,交AB于点E若∠BED=64°,则∠ADE的度数是( )
A、 B、 C、 D、4. 有4根长度分别为2、4、6、7的木条,从中任意选出三根,其中能构成三角形的有( )A、1种 B、2种 C、3种 D、4种5. 如图,AD是△ABC的角平分线,AC∥DE,交AB于点E若∠BED=64°,则∠ADE的度数是( ) A、23° B、26° C、32° D、37°6. 在 中, ,则 是( )A、直角三角形 B、锐角三角形 C、钝角三角形 D、等腰三角形7. 如图,点在的延长线上,交于点 , 交于点 , 若 , , 则的度数为( )
A、23° B、26° C、32° D、37°6. 在 中, ,则 是( )A、直角三角形 B、锐角三角形 C、钝角三角形 D、等腰三角形7. 如图,点在的延长线上,交于点 , 交于点 , 若 , , 则的度数为( ) A、 B、 C、 D、8. 如图, , 、、分别平分、、 . 以下结论,其中正确的是( )
A、 B、 C、 D、8. 如图, , 、、分别平分、、 . 以下结论,其中正确的是( )①;②;③;④ .
 A、①② B、②③④ C、①③④ D、①②③④9. 如图,线段AB、CD相交于点O , 连接AD、CB , 和∠BCD的平分线AP和CP相交于点P , 则∠P与∠D、∠B之间存在的数量关系为( )
A、①② B、②③④ C、①③④ D、①②③④9. 如图,线段AB、CD相交于点O , 连接AD、CB , 和∠BCD的平分线AP和CP相交于点P , 则∠P与∠D、∠B之间存在的数量关系为( ) A、 B、 C、 D、10. 如图,在中, , 分别平分 , , 交于 , 为外角的平分线,的延长线交于点 , 记 , , 则以下结论:①;②;③;④.正确的是( )
A、 B、 C、 D、10. 如图,在中, , 分别平分 , , 交于 , 为外角的平分线,的延长线交于点 , 记 , , 则以下结论:①;②;③;④.正确的是( )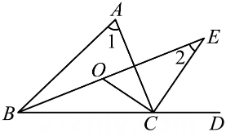 A、①④ B、①②③ C、①③④ D、①②④
A、①④ B、①②③ C、①③④ D、①②④二、填空题:本大题共5小题,每小题3分,共15分.
-
11. 如图,∠ACD是△ABC的外角,若∠ACD=110°,∠A=80°,则∠B=°.
 12. 在中, , 则 .13. 如图,是的边上的中线,是的边上的中线,是的边上的中线,连接 , . 若的面积是 , 则阴影部分的面积是 .
12. 在中, , 则 .13. 如图,是的边上的中线,是的边上的中线,是的边上的中线,连接 , . 若的面积是 , 则阴影部分的面积是 . 14. 如图所示,点 , , 分别是线段 , , 的中点,若的面积为 , 那么的面积为 . (用含的式子表示)
14. 如图所示,点 , , 分别是线段 , , 的中点,若的面积为 , 那么的面积为 . (用含的式子表示)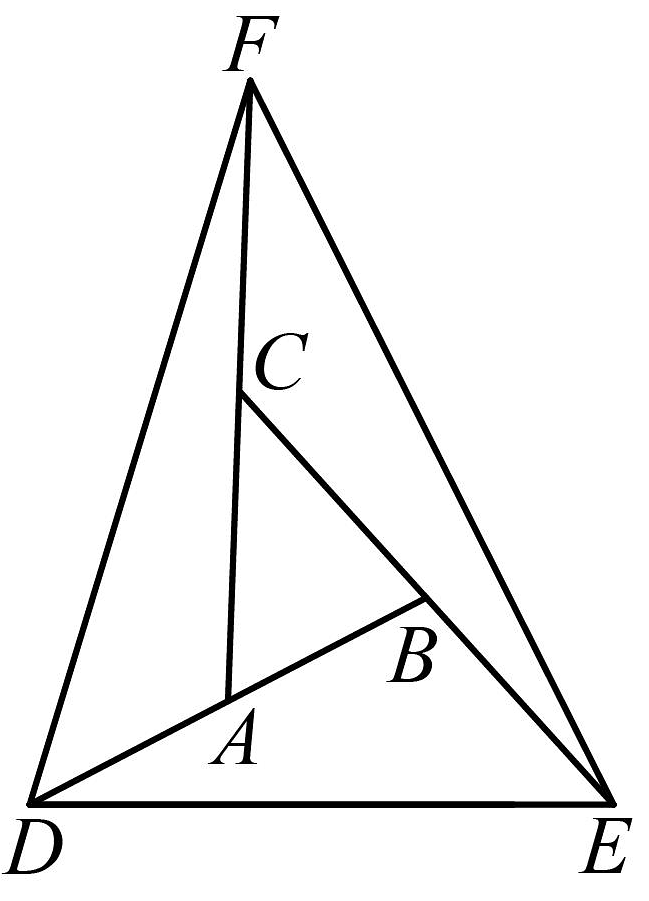 15. 如图1,六分仪是一种测量天体高度的航海仪器,观测者手持六分仪,可得出观测点的地理坐标.
15. 如图1,六分仪是一种测量天体高度的航海仪器,观测者手持六分仪,可得出观测点的地理坐标.在图2所示的“六分仪原理图”中,所观测星体记为S,两个反射镜面位于A,B两处,B处的镜面所在直线自动与刻度线保持平行(即),并与A处的镜面所在直线相交于点C,所在直线与水平线相交于点D, , 观测角=(用表示).


小贴士:
如图3,光线经过镜面反射时,反射角等于入射角,所以图2中 ,

三、解答题:本大题共8小题,共75分.
-
16. 如图,已知 , .
 (1)、求证:(2)、若 , , 求的度数.17. 如图, 在△ABC 中, AD 是高, AE, BF 是角平分线, 且AE, BF 相交于点O,∠BAC=50°, ∠C=70°. 求∠DAC 和∠BOA 的度数.
(1)、求证:(2)、若 , , 求的度数.17. 如图, 在△ABC 中, AD 是高, AE, BF 是角平分线, 且AE, BF 相交于点O,∠BAC=50°, ∠C=70°. 求∠DAC 和∠BOA 的度数. 18. 如图,在中, , 三个内角的平分线交于点O.
18. 如图,在中, , 三个内角的平分线交于点O.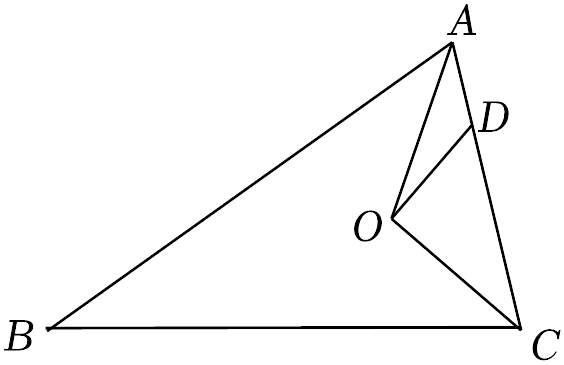 (1)、若 , 求的度数;(2)、过点O作 , 交于点D.试说明: .19. 如图,BD是△ABC的角平分线,DE∥BC,交AB于点E.
(1)、若 , 求的度数;(2)、过点O作 , 交于点D.试说明: .19. 如图,BD是△ABC的角平分线,DE∥BC,交AB于点E.(1)若∠A=40°,∠BDC=60°,求∠BED的度数;
(2)若∠A-∠ABD=20°,∠EDC=65° ,求∠A的度数.
 20. 如图,在△ABC中,AD是△ABC的高线,AE是△ABC的角平分线.已知∠BAC=80°,∠C=40°.求∠DAE的大小.
20. 如图,在△ABC中,AD是△ABC的高线,AE是△ABC的角平分线.已知∠BAC=80°,∠C=40°.求∠DAE的大小. 21. 如图 , 在中,与的平分线相交于点 .
21. 如图 , 在中,与的平分线相交于点 . (1)、若 , 则的度数是 ;(2)、如图 , 作外角 , 的角平分线交于点 , 试探索 , 之间的数量关系;(3)、如图 , 延长线段 , 交于点 , 在中,存在一个内角等于另一个内角的倍,求的度数.22. 如图,已知 , 点C在上,点A、B在上.在中, , , 点E、F在直线上,在中, , .
(1)、若 , 则的度数是 ;(2)、如图 , 作外角 , 的角平分线交于点 , 试探索 , 之间的数量关系;(3)、如图 , 延长线段 , 交于点 , 在中,存在一个内角等于另一个内角的倍,求的度数.22. 如图,已知 , 点C在上,点A、B在上.在中, , , 点E、F在直线上,在中, , . (1)、图中的度数是多少;(2)、将沿直线平移,当点D在上时,求的度数;(3)、将沿直线平移,当以C、D、F为顶点的三角形中有两个角相等时,请直接写出的度数.23. 综合与实践
(1)、图中的度数是多少;(2)、将沿直线平移,当点D在上时,求的度数;(3)、将沿直线平移,当以C、D、F为顶点的三角形中有两个角相等时,请直接写出的度数.23. 综合与实践【知识生成】三角形的中线把三角形分成面积相等的两部分.
已知:如图1,在△ABC中,点D是BC边上的中点,连接AD . 求证:S△ABD=S△ACD .
证明:过点A作AE⊥BC于E
∵点D是BC边上的中点
∴BD=CD
∵
∴S△ABD=S△ACD

【拓展探究】
(1)、如图2,在△ABC中,点D是BC边上的中点,若S△ABC=6,S△ABD=;(2)、如图3,在△ABC中,点D是BC边上的点且CD=2BD , S△ABD和S△ABC存在怎样的数量关系?请模仿写出证明过程;(3)、【问题解决】现在有一块四边形土地ABCD(如图4),熊大和熊二都想问老熊要这块地,老熊让他们平分,可他们谁都没法平分,请你来帮帮忙.
要求:用不超过三条的线段画出平分方法,并对作法进行描述.可利用带刻度的直尺.